KCL rätt beräknat?
Hej,
Jag håller på med denna uppgift och har fastnat lite på ifall jag beräknat KCL:n rätt. Detta är uppgiften:
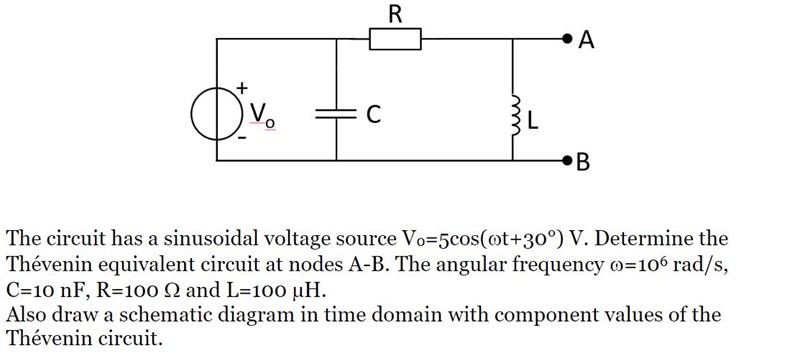
Jag har kommit såhär långt:

Då är det KCL jag tänker på? Har jag tänkt rätt till här?
Hejsan
Vth kan väl räknas ut som spänningsdelning av V0 över R och jwL? Kapacitansen har ingen inverkan på uträkningen av Vth väl?
När du anger V0 på polär form, spelar det in att V0 är angiven som en cosinus? Blir argumentet 30 grader eller ska man räkna om till sinus? Är lite osäker på detta själv.
Hej Thomas!
Jag fick fram att man kunde använda voltage divider formula, som du förklarat, och fick då Vth = V0 * ZL/R+ZL.
Jag fastande återigen är här: 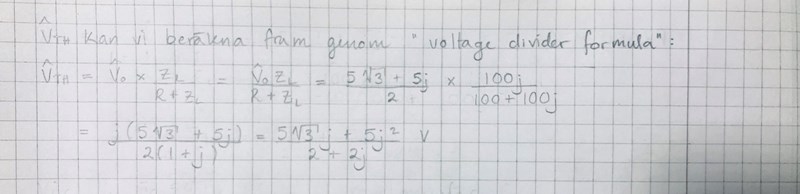
och fick en liten ledtråd av min lärare att jag hellre behåller polär form på cosinus funktionen alltså 5 < 30 och försöker utvärdera 100j/100+100j och för om den till polär form.
Däremot får jag inte till det i polär form?
Hej!
Jag om du multiplicerar med konjugatet (tror jag det heter) till 2 + 2j över och under bråkstrecket så slipper du den komplexa nämnaren.
Klockan börjar bli mycket nu, jag får nog be att få fortsätta i morgon.
Hej!
Ja det tycker jag också! Vi ses imorgon:)
Hej Tomas!
Jag tänkte mer hur jag kan göra om 100j/100+100j till polär form. Jag försökte multiplicera med konjugatet som borde vara 100-100j/100-100j, man jag får det bara till ett ensamt (j). Vilket inte kan stämma.
Konjugatet är väl bara 100-100j?
Om du multiplicerar detta med både täljare och nämnare:
Sen ska du kunna räkna på och få de på formen a+bj
Hej,
Jag tror du missade ett (j) i täljaren. Jag fick det till detta:
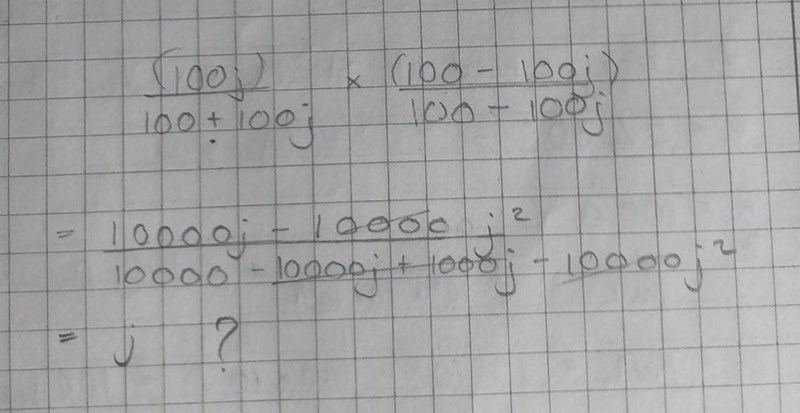
Ledsen om det är slarvigt skrivet, jag var lite snabb!
Vet du vad j2 blir?
Oj ja, j^2 är ju -1. Vänta jag återkommer.
Nu fick jag det till 0.5j + 0.5. Om jag tänkt rätt bör det i polär form bli:
(0.5j+0.5) = A
A = = 0.70710...
= = 45
Så polär form bör vara: 0.7
Tänker jag rätt?
Ser bra ut!
Tänk att en liten miss med j, kunde göra så mycket!
Nu måste jag fråga lite om när man ska finna Rth, eller jag kanske ska kalla den Zth (med tanke på impedansen).
Jag tänker att R är i serie med kondenstorn och de i sin tur i parallell med .
Men jag har lite svårt att tänka hur jag ska sätta ihop allt. Ska jag tänka på "resistorer"?
Där är nog en liten klurighet i denna uppgiften. Kolla hur man gör för att räkna ut Rth:
https://sv.wikipedia.org/wiki/Th%C3%A9venins_teorem
Speciellt steg 3 i exemplet
Jo, men precis. I och med att det inte finns någon beroende källa så kan vi sätta till 0 V i mitt problem. Precis som de gjort på bilden i steg 3, så är den inte där. Så kvar blir ju resistorerna som de räknat till .
I mitt problem så ska man ju "kolla in" genom nod A och B och sen avgöra impedansen som man ser.
Jag tänker att kvar blir ju , och som man ser när man kollar in genom A och B.
Då tänker jag att och om jag då ska betrakta impedansen av kondensatorn och induktorn som "resistorer" kanske?
Jag får erkänna att jag är lite rostig på att använda Theveninekvivalenter men om jag förstått rätt så behöver man inte bry sig om Zc i och med att spänningskällan betraktas som en kortslutning när man ska beräkna Rth. Kvar blir R ∥ ZL.
Impedans är ju ett namn på en komponent där R, L och C ingår i olika kombinationer. En resistans kan man ju säga är ett specialfall av en impedans. Man kan räkna på impedanser precis som med resistanser när det gäller serie och parallellkoppling. Det blir lite mer komplicerat bara.
Nej, men det är inga problem.
Du har givit mig mycket kunskap alla gånger du hjälpt mig och det är jag tacksam för! :) Så lite ringrostig får man vara tycker jag!
Ja, jag tänkte ifall jag skulle "ta med" Zc i mina beräkningar för Rth, men jag var faktiskt osäker på det.
ThomasN skrev:Impedans är ju ett namn på en komponent där R, L och C ingår i olika kombinationer. En resistans kan man ju säga är ett specialfall av en impedans. Man kan räkna på impedanser precis som med resistanser när det gäller serie och parallellkoppling. Det blir lite mer komplicerat bara.
Ja, okej då förstår jag!
Nilo skrev:Jo, men precis. I och med att det inte finns någon beroende källa så kan vi sätta till 0 V i mitt problem. Precis som de gjort på bilden i steg 3, så är den inte där. Så kvar blir ju resistorerna som de räknat till .
I mitt problem så ska man ju "kolla in" genom nod A och B och sen avgöra impedansen som man ser.
Jag tänker att kvar blir ju , och som man ser när man kollar in genom A och B.
Då tänker jag att och om jag då ska betrakta impedansen av kondensatorn och induktorn som "resistorer" kanske?
varför räknar man inte Zth = R + ZL // Zc ?
det går väl samma ström över R och ZL så de borde väl vara i serie sen parallella med Zc , eller tänker jag fel?
Jag är lite osäker på den delen faktiskt, jag är inte hundra på ifall Zc ska tas med eller inte...
Nilo skrev:Jag är lite osäker på den delen faktiskt, jag är inte hundra på ifall Zc ska tas med eller inte...
jag tror den ska tas med men är osäker på vilka som är i serie samt parallella med vilka :S
edit: för det avgör sen om det ska vara en kondensator eller induktor i thevenin kretsen sen då imaginärdelen blir + eller - beroende vilka man väljer som parallella / serie
edit: eller det kanske inte spelar någon roll, de kanske blir samma resultat?
Nej, jag är helt ärligt också väldigt osäker både i det här med ifall Zc ska tas med och hur de ska räknas till Zth.
Nilo skrev:Nej, jag är helt ärligt också väldigt osäker både i det här med ifall Zc ska tas med och hur de ska räknas till Zth.
jag räknar med den och får Zth till = 100 - 100j alternativt Zth = 100 + 100j beroende på om jag väljer R+L // C eller R+C // L
Jag fick det till 50-50j.
Nilo skrev:Jag fick det till 50-50j.
Zth = R + L // C -->
så räknade jag men vet ej om det är fel
Jag räknade såhär:
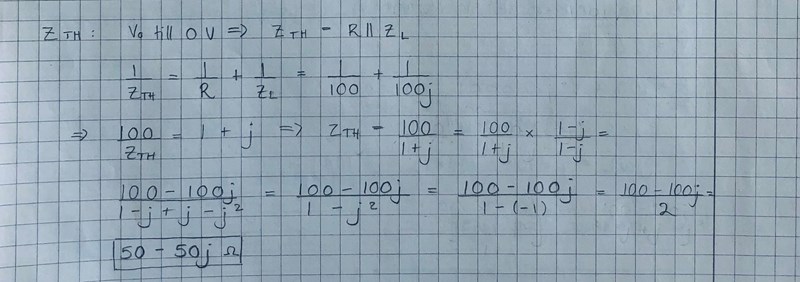
Nilo skrev:Jag räknade såhär:
exakt så räknade ej med kondensatorn?
Menar du att du räknade så men utan kondensatorn?
Får jag fråga vad du fick Vth till?
Nilo skrev:Menar du att du räknade så men utan kondensatorn?
Får jag fråga vad du fick Vth till?
nej jag räknade med kondensatorn men jag ser att du ej har gjort det i din Zth
min Vth blev
Okej då har vi fått samma Vth, men inte Zth. Intressant.
Maremare skrev:edit: för det avgör sen om det ska vara en kondensator eller induktor i thevenin kretsen sen då imaginärdelen blir + eller - beroende vilka man väljer som parallella / serie
Vill du förklara lite utförligare vad imaginärdelen (+/-) har för innebörd, och hur man vet beroende på det om det är kondensator eller induktor?
Och hur de då kopplas i slutliga Thévenin kretsen?
Jag har för mig att om imaginärdelen är + så är det en kondensator i serie med en resistor och sedan spänningskällan.
Men jag kanske är ute och cyklar?
Nilo skrev:Jag räknade såhär:
Tecknet på imaginärdelen?
Oj men om imaginärdelen är positiv, innebär det att det är en induktans i parallell med spänningskällan i thévenin ekvivalenten?
VTH tycks bli en spänningsdelning av V0
Oj men om imaginärdelen är positiv, innebär det att det är en induktans i parallell med spänningskällan i thévenin ekvivalenten?
Sett från A-B finns en induktans parallellt i serie med en resistans.
Kapacitansen ses som kortsluten av spänningskällan.
Förstår jag rätt ifall den slutgiltiga Thévenin kretsen ser ut såhär?
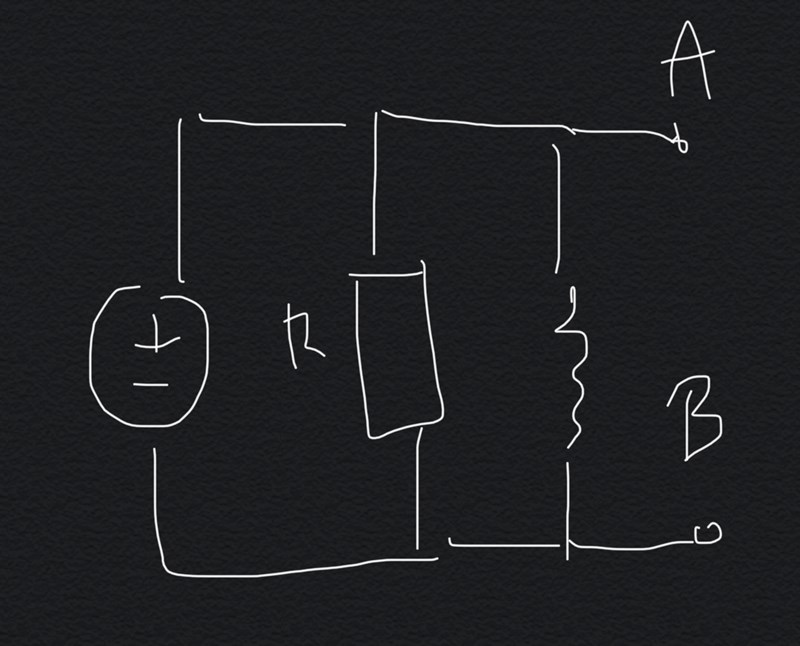
Och jag tror även att jag då räknat fel, alltså att induktans ska räknas ut istället för kondensator.
Stämmer det?
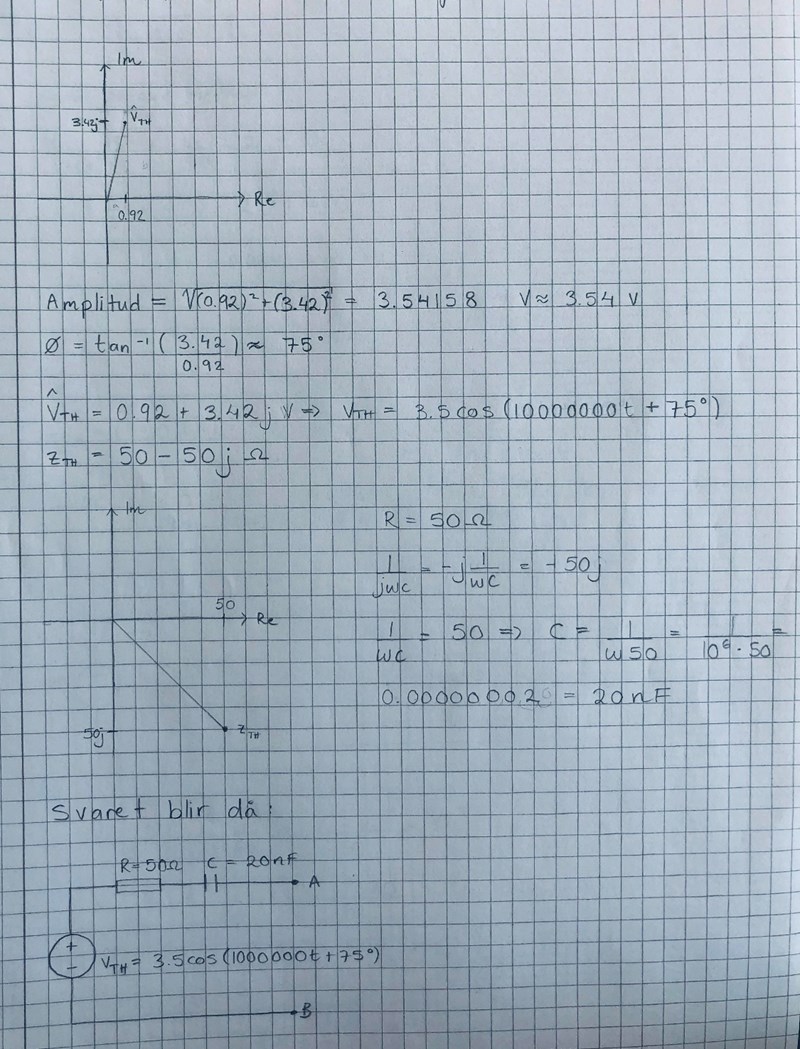
Nilo skrev:Förstår jag rätt ifall den slutgiltiga Thévenin kretsen ser ut såhär?
I mina beräkningar av Zth placerar jag induktans i serie med resistans
Affe Jkpg skrev:
Sett från A-B finns en induktans parallellt med en resistans.
Förlåt, nu blir jag lite förvirrad. Blir det alltså:
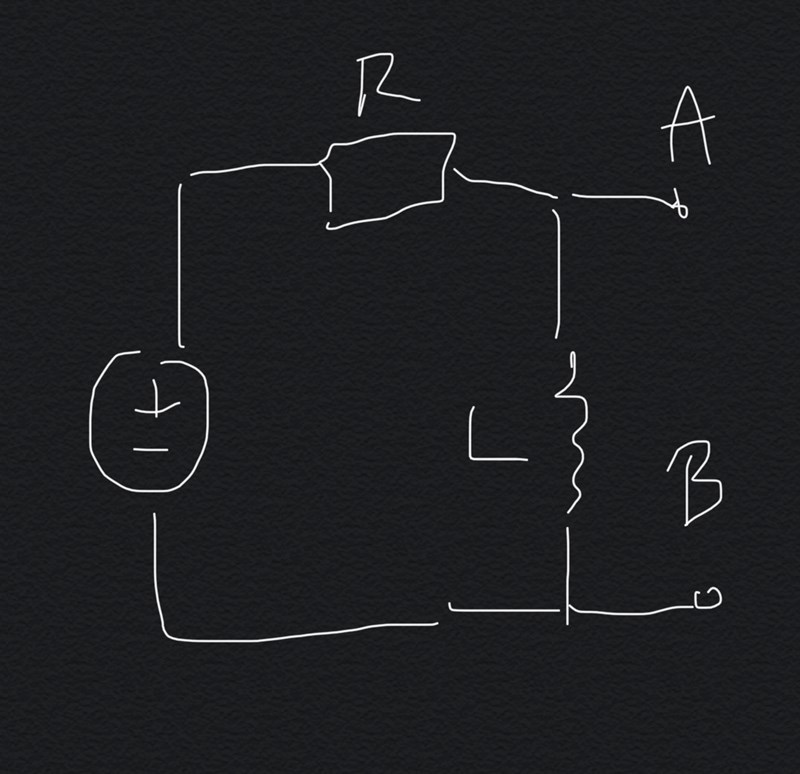
Stämmer det?
Nä, som jag beskrivit tidigare:
VTH tycks blir en spänningsdelning av V0
Nilo skrev:Affe Jkpg skrev:Sett från A-B finns en induktans parallellt med en resistans.
Förlåt, nu blir jag lite förvirrad. Blir det alltså:
Ursäkta, jag ser nu att jag skrev fel förut. Jag menar detta: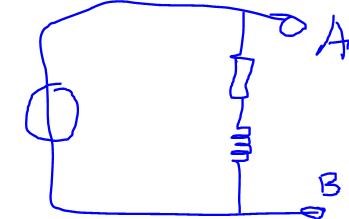
 Precis, jag är med på det. Men slutligen så måste man ju rita kretsen för Thévenin impedansen. Egentligen är denna sida förre den jag skickade tidigare. Så egentligen är detta sida 2 och det i tidigare inlägget sida 3.
Precis, jag är med på det. Men slutligen så måste man ju rita kretsen för Thévenin impedansen. Egentligen är denna sida förre den jag skickade tidigare. Så egentligen är detta sida 2 och det i tidigare inlägget sida 3.
Affe Jkpg skrev:Nilo skrev:Affe Jkpg skrev:Sett från A-B finns en induktans parallellt med en resistans.
Förlåt, nu blir jag lite förvirrad. Blir det alltså:
Ursäkta, jag ser nu att jag skrev fel förut:
Ja okej! Då hänger jag med! Ingen fara! :)
Jag antar att man beräknar induktansen med formeln: jwL för att få fram rätt svar?
Jag antar att man beräknar induktansen med formeln: jwL för att få fram rätt svar?
Jag har tidigare svarat på Zth med :
Zth = 50*(1+j)
Thevenin-induktansen representeras då av 50j
Ja okej, sorry. Är lite väl trött just nu. Tack för hjälpen och nu ska jag ta och sova!
God natt!! :)



