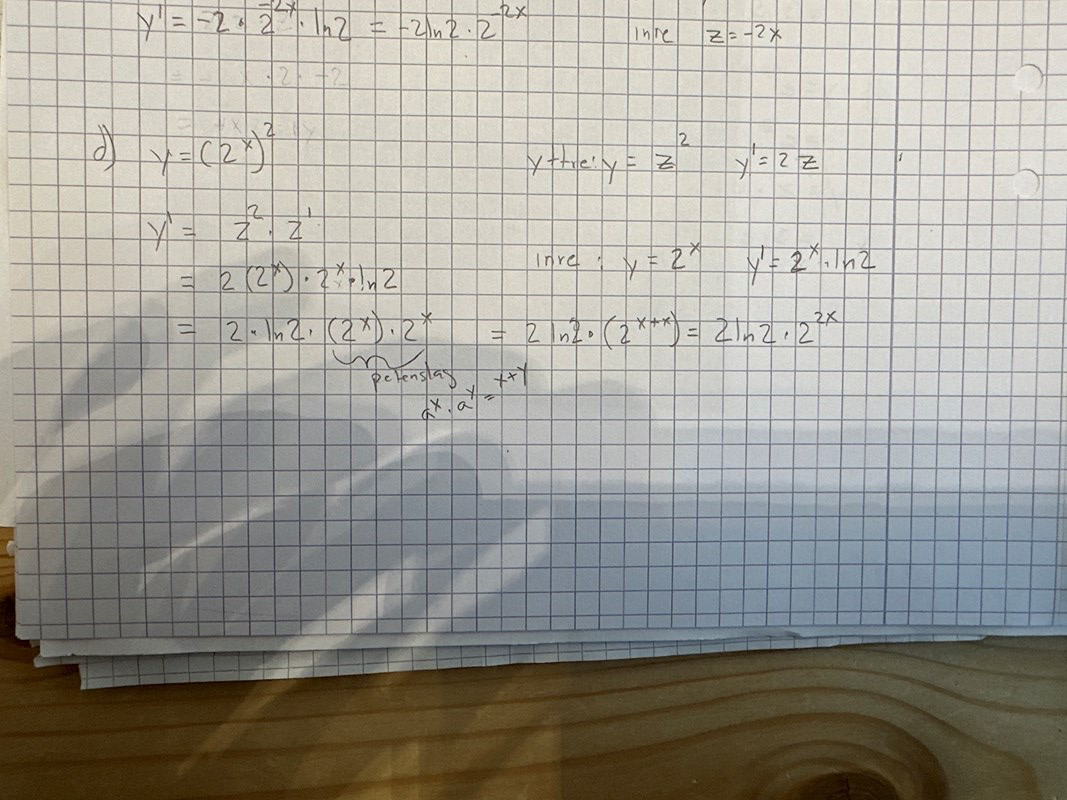4
svar
98
visningar
Kedjeregeln

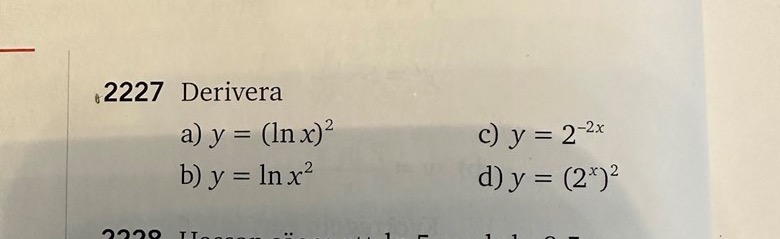
hejsan
skulle behöva ha hjälp med d)
är det två funktioner sammansatta?
Ja, du kan se det så. Börja med att skriva om uttrycket med hjälp av lämplig potenslag.
Ett annat sätt att se det är att använda produktregeln om du har lärt dig den.
Bra kontroll är att använda båda metoderna och se om du får samma resultat.
Ditt resultat stämmer och dina tankebanor är troligtvis korrekta, men det är lite svårt att följa dem.
Förslag på beskrivning av lösningen:
(potenslag)
Sätt nu .
Då är och kedjeregeln ger oss:
Eftersom
så är
så är
Det ger oss
=====
Har du prövat att derivera med produktregeln?
Har inte testa med produktregeln