Kedjeregeln och parenteser

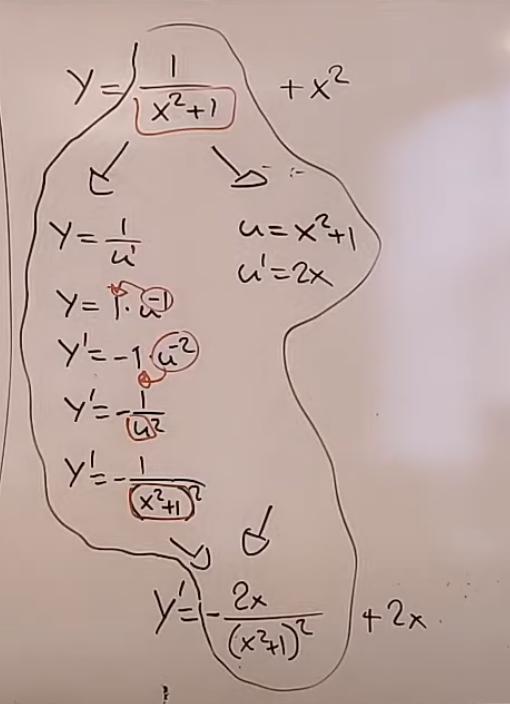Man ska tillämpa kedjeregeln på $\frac{1}{(x^{2} + 1)}$ . Detta är facit.

Jag gjorde rätt hela vägen och fick rätt svar men min fråga är angående att flytta ut minustecknet ur parentesen. När man får $- 1 \cdot u^{- 2}$ i steg 3 i VL så multiplicerade jag in -1 i parentesen och fick då $\frac{1}{{(- x^{2} - 1)}^{2}}$ Vill
bara försäkra mig om att man då kan plocka ut minustecknet och sätta det framför bråket. Bevisligen kan man det men undrar väl ungefär varför eller hur det funkar..

Och hur kan man undersöka det, genom att sätta in siffror?

Jag får det inte till samma resultat om jag sätter in exempelvis x = 3

$\frac{1}{{(- 3^{2} - 1)}^{2}} = \frac{1}{64} - \frac{1}{{(3^{2} + 1)}^{2}} = - \frac{1}{100}$

Det är distributiva lagen. Samma lag alltså som t ex tillåter dig skriva 3•24=3(20+4)=60+4

men det där stämmer väl inte. 3 måste multipliceras med båda termerna?

Ja, det blev nog ett skrivfel där, i all hast av Tomten

Jag förvirrar mig i all text. Vad var frågeställningen?

Att "ta in" ett minustecken och sedan kvadrera bort det är inte helt rakt fram. Här får man vara aktsam med vad man gör.

-(a+b)^2 = (-(a+b))^2

är ej (allmänt) sant.

Ledsen, var svårt att formulera något tydligt

Är det läraren som skrivit på tavlan?

Exakt

Det är denna jag frågar om. Jag skrev ut u i det steget och multiplicerade in -1 i parentesen

Be "hen" söka nytt jobb, som vaktmästare eller något mera lämpligt.

Inget fel på vaktmästare. Min omskrivning dock, $\frac{1}{{(- x^{2} - 1)}^{2}} = - \frac{1}{{(x^{2} + 1)}^{2}}$
Stämmer alltså inte?

eddberlu skrev:
Inget fel på vaktmästare. Min omskrivning dock, $\frac{1}{{(- x^{2} - 1)}^{2}} = - \frac{1}{{(x^{2} + 1)}^{2}}$
Stämmer alltså inte?

Nej

VL är alltid >0

HL är alltid <0

Förstår inte varför det blir fel dock. Jag följer ju alla regler tekniskt sett. $- 1 \cdot {(x^{2} + 1)}^{2} ä r j u {(- x^{2} - 1)}^{2}$

eddberlu skrev:
Förstår inte varför det blir fel dock. Jag följer ju alla regler tekniskt sett. $- 1 \cdot {(x^{2} + 1)}^{2} ä r j u {(- x^{2} - 1)}^{2}$

Nej, du gör ett misstag där.

Du vet potenslagen

a^2 * b^2 = (ab)^2

(-1)^2 * (x^2+1)^2 = ( (-1)(x^2+1) )^2 = ( -x^2-1 )^2

Men du har inte (-1)^2 framför, du har bara -1.

(Däremot är

(-1) * (x^2+1)^2 =i^2 * (x^2+1)^2 = ( i(x^2+1) )^2

där i är den komplexa enheten.)

aaaha, så du menar att jag -1:an kommer ner som subtraktion och inte multiplikation? Eller varför annars får den inte parentes kring sig? derivatan av x^2 är ju 2·x eller x+x.

eddberlu skrev:
aaaha, så du menar att jag -1:an kommer ner som subtraktion och inte multiplikation? Eller varför annars får den inte parentes kring sig? derivatan av x^2 är ju 2·x eller x+x.

Vi pratar nog om helt skilda saker. Det ena är ren algebra hur man kan manipulera uttryck etc. Det andra är deriveringsregler.

y = 1/u = u^(-1)

y' = (-1)u^(-1-1)*u' = -u^(-2)*(2x) = -(x^2+1)^(-2)*(2x) = -1/(x^2+1)^2 * 2x = = -2x/(x^2+1)^2.

Säkert. Ah jag förstår inte riktigt vad det är du redovisar. Speciellt inte i nedre uttrycket.

Är du med på det som står i inlägg #16? Det finns ingen kvot eller derivata där.

Nej jag e nog inte med på varför -1 inte är (-1) i -1 · (x^2 +1)^2

Du kan ha parenteser runt -1 där om du vill. Det gör ingen skillnad.

Så varför blir det olika svar? är -1 (x^2+1)^2 inte (-x^2-1)^2?

Nej, och det står varför i #16 (tycker jag).

Svara

Visa senaste svar