Kinetisk friktion
Jag bestämmer den statiska friktionskoefficienten med enkelhet genom att rita ett frikroppsdiagram och sätta krafterna i x-led lika.
Jag får då: (korrekt enligt facit).
Däremot har jag ingen aning om hur jag ska bestämma . Jag har bara lärt mig att precis som , men vet att är lite mindre än .
Normalkraften är väl samma fast att massan börjar röra på sig? Förändras friktionskraften?
Hur kan man beräkna detta?
Jag spånar lite fritt så kanske du kommer vidare, jag har inget svar än för jag har inte räknat
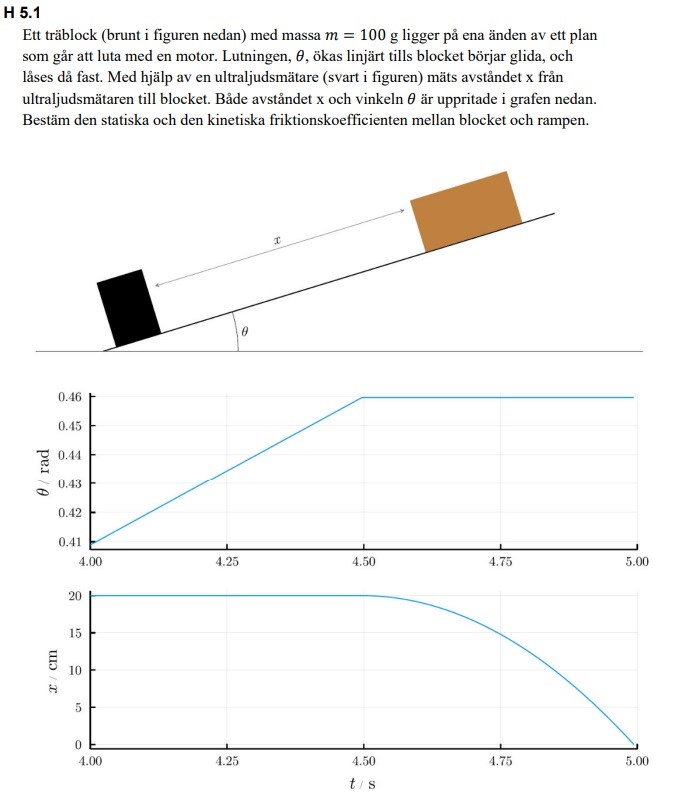
När klossen börjat röra sig så stannar motorn vid en viss vinkel. Eftersom normalkraften bara beror av vinkeln och klossens vikt, så kommer normalkraft och friktionskraft att vara konstanta. Men eftersom friktionskoefficienten är lite mindre än den statiska, så kommer den resulterande kraften på klossen att ge den en acceleration nedför planet. Den accelerationen borde man kunna utläsa ur x-t-grafen.
Kommer du vidare?
jonnefcb skrev:Förändras friktionskraften?
Hur kan man beräkna detta?
Ja, friktionskoefficienten kan ändras, är ofta lägre än för statisk friktion.
Ur dessa data kan man nog uppskatta vad träblockets acceleration är vid 0,46 radian.
Du kan modellera det som att friktionskraften som verkar på objektet approximativt är lika med:
Utifrån detta kan du härleda rörelseekvationer från Newtons andra lag. Det ser ut som om beteendet för liknar en andragradskurva av något slag. Detta borde vara bekant då det bör likna sträckformeln från gymnasiefysik då accelerationen är konstant.
Accelerationen bör vara konstant så jag sätter (med räknat från tiden då massan börjar glida).
.
Jag får alltså en acceleration i negativt x-led (neråt vänster i bild).
. Förstår inte riktigt. Är detta så mycket som friktionskraften har sjunkit med?
Hur som helst, den nya (kinetiska) friktionskraften blir isf .
Jag får slutligen . Facit säger 0,314.
Har jag gjort rätt?
Det är rätt.
Men jag förstår inte riktigt varför facit envisas med att använda tre värdesiffror i sitt svar då det är manuellt avlästa ingångsvärden ifrån en graf. (Du får samma svar i tredje decimalen om du använder den oavrundade statiska koefficienten , och g=9.82.)
jonnefcb skrev:Hur som helst, den nya (kinetiska) friktionskraften blir isf .
Jag får slutligen . Facit säger 0,314.
Har jag gjort rätt?
Jag skulle formulera det utan att blanda i koefficienten för statisk friktion.
Tyngdkraftens komposant parallellt med ytan är .
Kraften vid kinetisk friktion blir Det blir förstås samma sak.




