Klurig differentialekvation - vad menas med att "värdet stabiliseras?"

Har löst självaste differentialekvationen.
y' = 4,8 - 800y/(30 000 - 200t).
Lösningskurvans utseende:
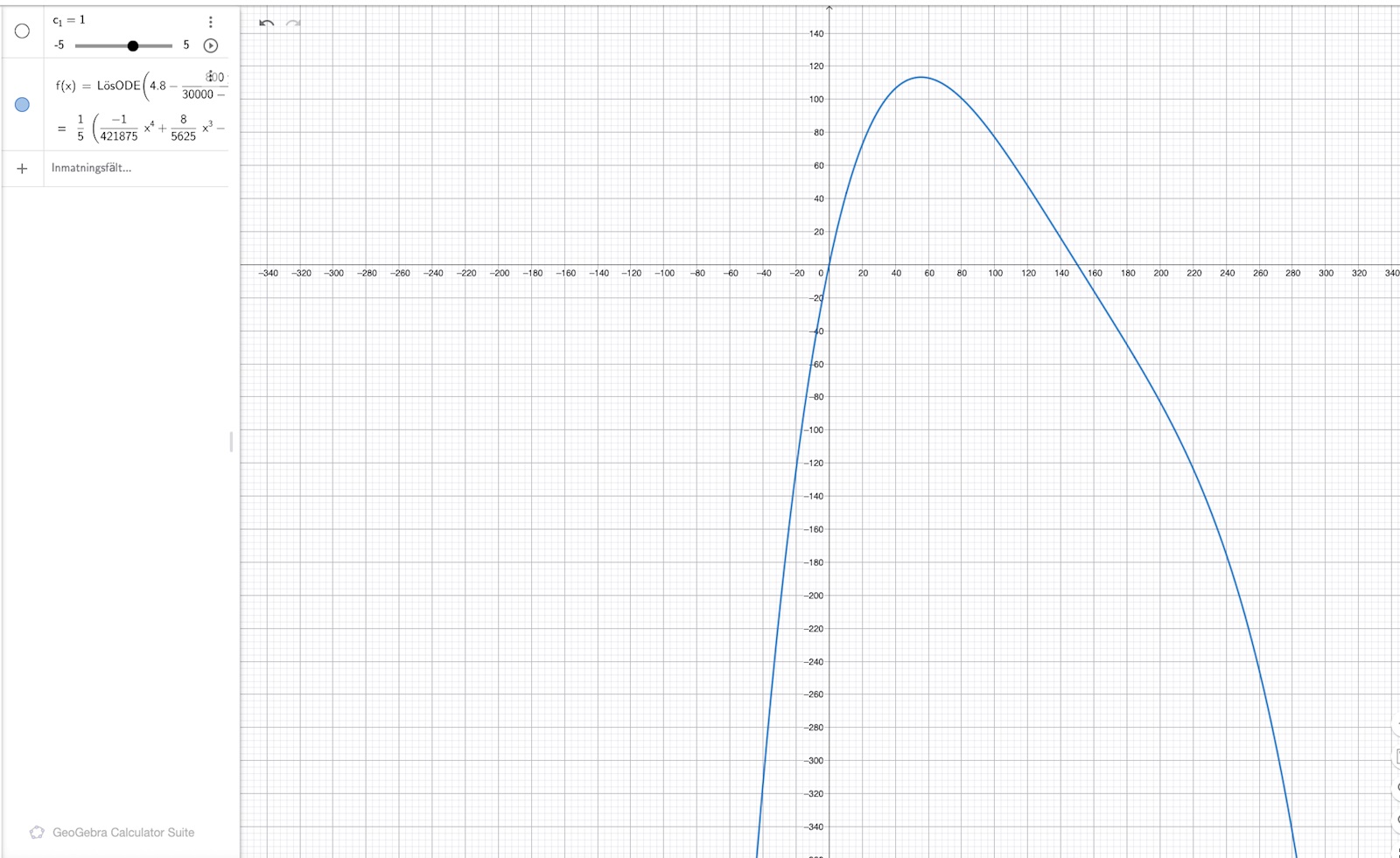
När stabiliseras värdet? Då x blir stort går inte y - värdet mot ett tydligt tal.
Menar du att mängden föroreningar är negativ efter t = 150?
Enligt facit stämmer lösningsekvationen...
Vilken del av grafen ska jag titta på? Är det extrempunkten? varför?
Tanken är tom efter 150 s, inser jag nu. Ja, jag vet inte heller vad som menas med "stabiliseras".
Hur ser kurvan för andelen förorening ut, förresten? Den du har anger totala mängden, antar jag.
Anonym_15 skrev:Enligt facit stämmer lösningsekvationen...
Säger facit något mer? Jag tror de avser R(t)=y'/V(t) där V(t) är volymen vid tiden t, då får man
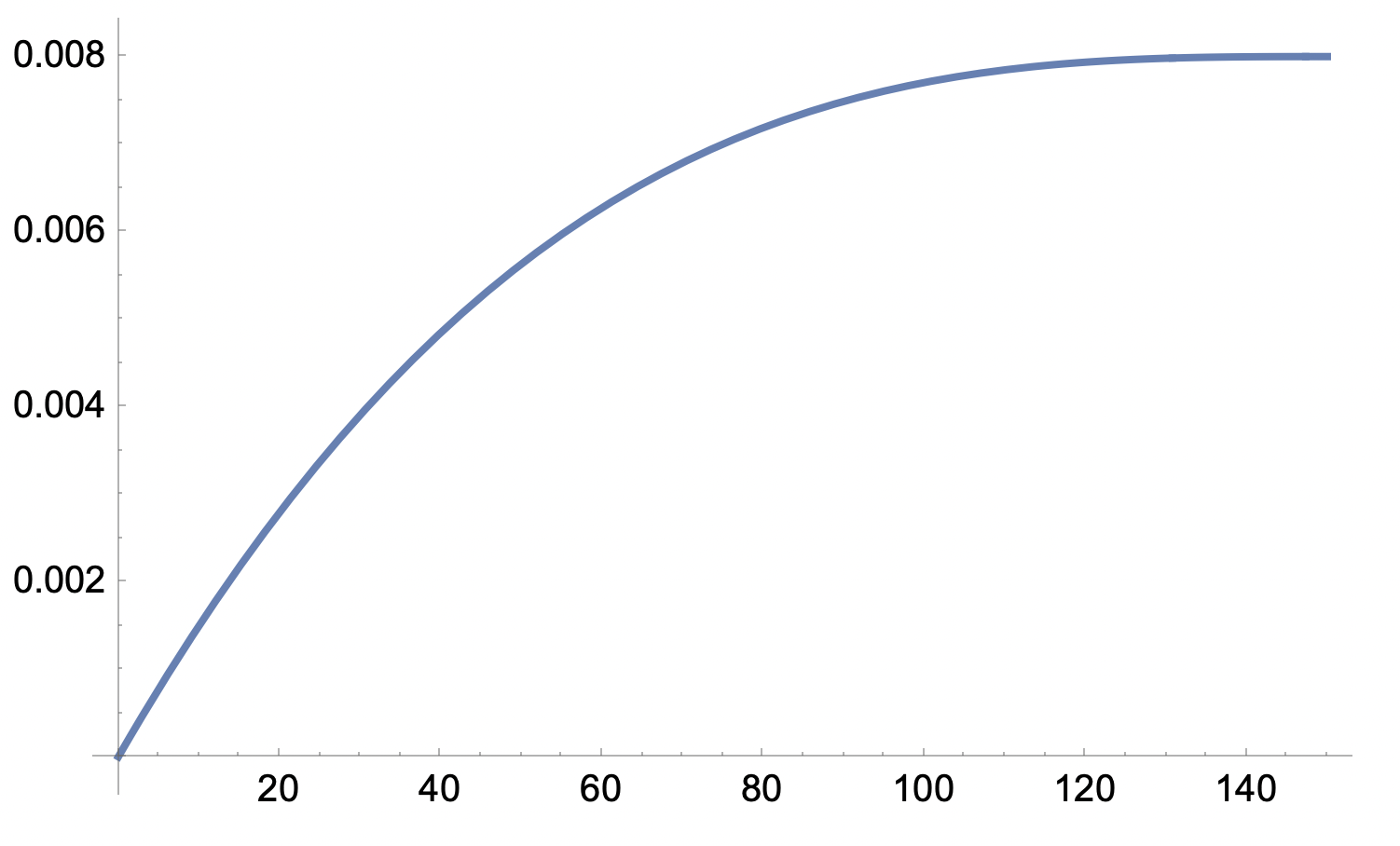
och då borde t=120 min. vara ett ungefärligt svar.
Redan vid 100, tycker jag. Det är nog det de menar, men "mängden föroreningar" är något annat.
Dessutom är uppgiften konstig. Om man vill tömma tanken så tömmer man den väl bara, och fyller inte på med nåt som ändå snart ska tömmas ut.
Laguna skrev:Redan vid 100, tycker jag. Det är nog det de menar, men "mängden föroreningar" är något annat.
Håller med. Dålig formulering.
Anonym_15 skrev:Enligt facit stämmer lösningsekvationen...
I min bok säger facit bara

Uppgiften är minsann felformulerad med tanke på att vattentanken blir tom efter 2,5 timmar.
Jag hittade tyvärr ingen rättelselista till boken Matematik 5000+ kurs 5 på Natur och Kulturs webbsidor (och inte heller på nokportalen.se)
Så här dåligt blir det ofta när man försöker skriva en matematikuppgift med slarvigt vardagsspråk.
Jag skulle svara att mängden BÖRJAR stabiliseras direkt, vid t=0.
LuMa07 skrev:Anonym_15 skrev:Enligt facit stämmer lösningsekvationen...
I min bok säger facit bara
Uppgiften är minsann felformulerad med tanke på att vattentanken blir tom efter 2,5 timmar.
Jag hittade tyvärr ingen rättelselista till boken Matematik 5000+ kurs 5 på Natur och Kulturs webbsidor (och inte heller på nokportalen.se)
De har nog fullt fokus på 7000 nu och lämnar 5000 åt sitt öde. Vi får se när 7000 kommer.
troligen ska det vara lika stort utflöde som inflöde i tanken.
Om man sätter utflödet till 600 l/min får man ett svar som överensstämmer med facits dvs cirka 4 timmar
Under dagen fick jag tag i en gammal kursbok: Matematik 3000 kurs E som gavs ut 2002. Jag hittade uppgiften där, fast med en annan frågeställning.

Följande står i facit:

Jag antar att man ville modernisera uppgiften, men har inte riktigt lyckats med det. (Jag har inte åtkomst till Matematik 4000 eller 5000 blå, så jag vet inte när exakt ändringen skedde)
LuMa07 skrev:Under dagen fick jag tag i en gammal kursbok: Matematik 3000 kurs E som gavs ut 2002. Jag hittade uppgiften där, fast med en annan frågeställning.
Följande står i facit:
Jag antar att man ville modernisera uppgiften, men har inte riktigt lyckats med det. (Jag har inte åtkomst till Matematik 4000 eller 5000 blå, så jag vet inte när exakt ändringen skedde)
Jag sitter med 5000, Ma4 (c) 2020 och just den förekommer ej här, även om de kort behandlar diff.ekv.
Jag hade ingen aning räknare 2002 kunde rita riktningsfält. Får spana in om min Casio kan det idag.




