Klurig integral

här är uppgiften. Försökte lösa, gav upp, frågade gemini som försökte lösa den på ett enkelt sätt 3 olika gånger, vilket den också misslyckades med. Den löste den till slut genom en ganska tung beräkning, men det är inte menat att jag ska kunna lösa uppgifterna sådär. Finns det en lätt lösning, eller har gemini rätt i att uppgiften kanske blev mycket svårare än tänkt?
Detta är en standarduppgift för variabelbytet som omvandlar integranden till ett rationellt uttryck i variabeln . Detta byte brukar dock kräva en hel del arbete.
Man behöver ha lite trigonometriska formler i sin verktygslåda:
- enligt trig:ettan. Detta medför att , vilket kommer att användas i omskrivningar med .
- Dubbla vinkelns formel för sinus ger att
- Dubbla vinkelns formel för cosinus ger att
Sambandet där är ekvivalent med där . Därmed blir .
När allt detta sätts ihop så fås:
Det första bråket förenklas genom att förlänga det med , vilket ger
.
Integralen blir därmed
Därefter är det "bara" partialbråksuppdelning och inga mer konstigheter.
Ifall det känns ointuitivt att dubbla vinkelns formler används, så kan man resonera också lite annorlunda för att hitta omskrivningar av sin x och cos x.
Man utgår från att är ekvivalent med med lämpliga intervall för och . Därmed blir
- , där man tydligt ser dubbla vinkeln, så
- , där man tydligt ser dubbla vinkeln, så
Det återstår att hitta och , vilket kan göras m.h.a. den rätvinkliga triangeln enligt följande figur:
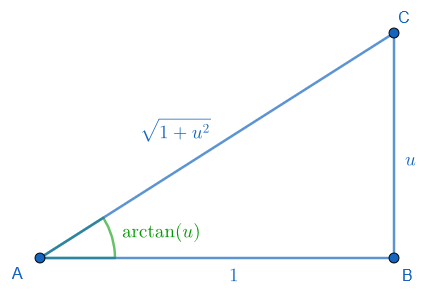
så och .

