Kluriga problem i geometri
Hur stor del av den största triangelns yta upptas av de tre färgade trianglarnas sammanlagda yta?
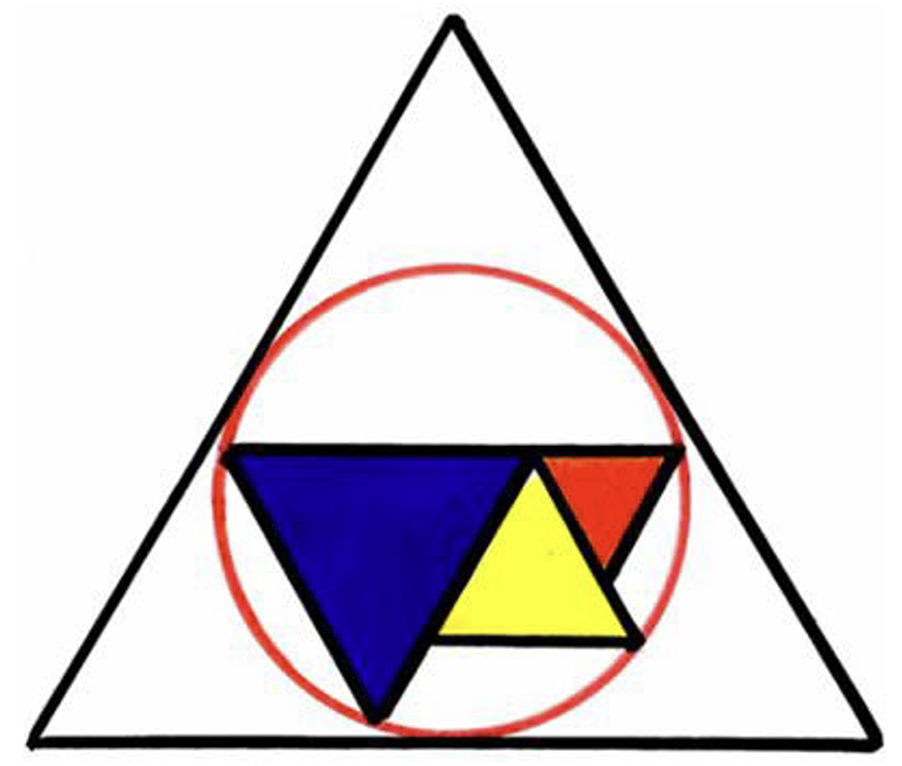
Bilden är lite missanpassad, det skall vara tangeringar etc. (som brukligt).
Visa spoiler
Ledtråd: Invariansprincipen.
Är det givet att alla trianglar är liksidiga?
Visa spoiler
Jag har en idé, men inget bevis än. Är svaret 1/4?
Om man antar att de tre färgade trianglarna är lika stora, så instämmer jag i Lagunas idé.
Det luriga tycker jag är att storleken på de tre liksidiga färgade trianglarna knappast kan väljas godtyckligt, då de bildar 4 punkter på cirkeln, men det räcker med 3 punkter för att bestämma dess radie.
Laguna skrev:Visa spoiler
Jag har en idé, men inget bevis än. Är svaret 1/4?
Ja, 1/4
Jag försöker finna någon analytiskt angreppspunkt på att beskriva figuren geometriskt (koordinater m.m.) men finner ingen bra start. Har ni någon idé?
Jag tänkte att man utgår från 3 (små) trianglar enligt bild med sidorna s1, s2, och s3.
Första problemet är att finna cirkelns medelpunkt, M.
M_x = 1/2(s1+s3)
men vi kan sätta den till M_x=0 för enkelhetens skull.
Givet 3 punkter kan man finna cirkelns ekvation, men hur kommer man vidare, på ett bra sätt och finner M?
Visa spoiler
Här är en idé där analytisk geometri blandats in för att visa att den sammanlagda arean inte beror av den exakta positionen av den vågräta sträckan som avgränsar den blå och den röda triangeln uppåt.
Låt oss anta att cirkeln är enhetscirkeln med mittpunkten i origo.
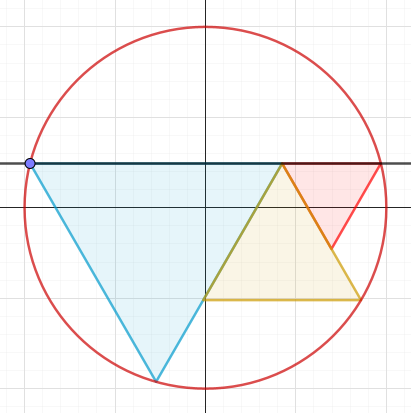
Steg 1:
Spegla röda triangeln i dess övre kant. (samma resultat fås ifall röda triangeln roteras med 60° medurs kring sitt högra hörn)

Steg 2:
Rotera den gula triangeln med 120° medurs kring dess övre hörn. (Samma resultat fås ifall den speglas i symmetrilinjen som kommer att dras i nästa steg.
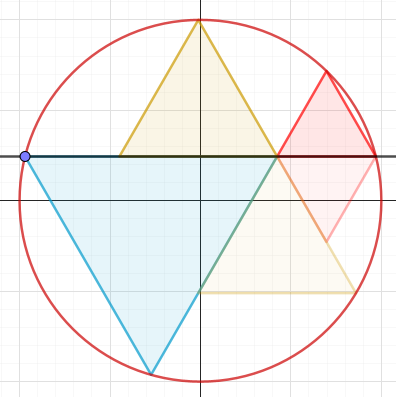
Steg 3:
Dra den symmetrilinje som är gemensam för den blå triangeln och spegelbilden för den röda triangeln.

Steg 4:
Rotera hela figuren med 60° moturs kring origo, så att den gemensamma symmetrilinjen är lodrät.
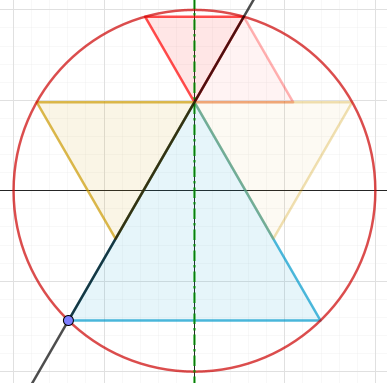
Steg 5:
Notera att symmetrilinjen och den vågräta sträckan som bildas av de gula trianglarnas övre kanter korsar varandra på y-axeln. Skärningspunktens y-koordinat ska kallas för .
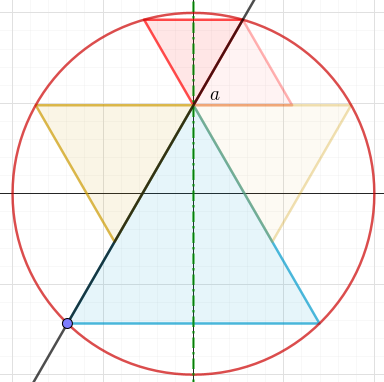
Steg 6:
Den svarta linjens ekvation är och den skär enhetscirkeln i punkterna där , d.v.s. . Skärningspunkternas -koordinater är därmed
Steg 7:
Sidlängderna på den blå och röda trianglarna är därmed
och
Steg 8:
Sidlängden på den gula triangeln beräknas enligt Pythagoras sats,
Steg 9:
En liksidig triangeln med sidlängden har arean . Den sammanlagda arean är alltså:
Slutsats:
Den sammanlagda arean beror ej av värdet på .
Ursprungsproblemet där cirkeln är inskriven i en stor liksidig triangel:
Om den inskrivna cirkeln är enhetscirkeln, så har den stora liksidiga triangeln sidlängden och arean .
Det sökta förhållandet blir:
.
Tillägg: 6 aug 2025 16:12
Nu har jag insett att man skulle kunna klara sig med exakt samma resonemang utan att rita någon spegelbild till den gula triangeln, d.v.s. Steg 2 är överflödigt. (Symmetrin är dock tydligare om man gör det)
Klurigt!
Jag kände jag behövde se det här framför mig lite större och tydligare, så jag konstruerade problemet i Geogebra. Eftersom vi kommit fram till att svaret är 1/4 så känns det inte som en spoiler.
Kanske kan större bilder hjälpa någon (eller mig) på traven.
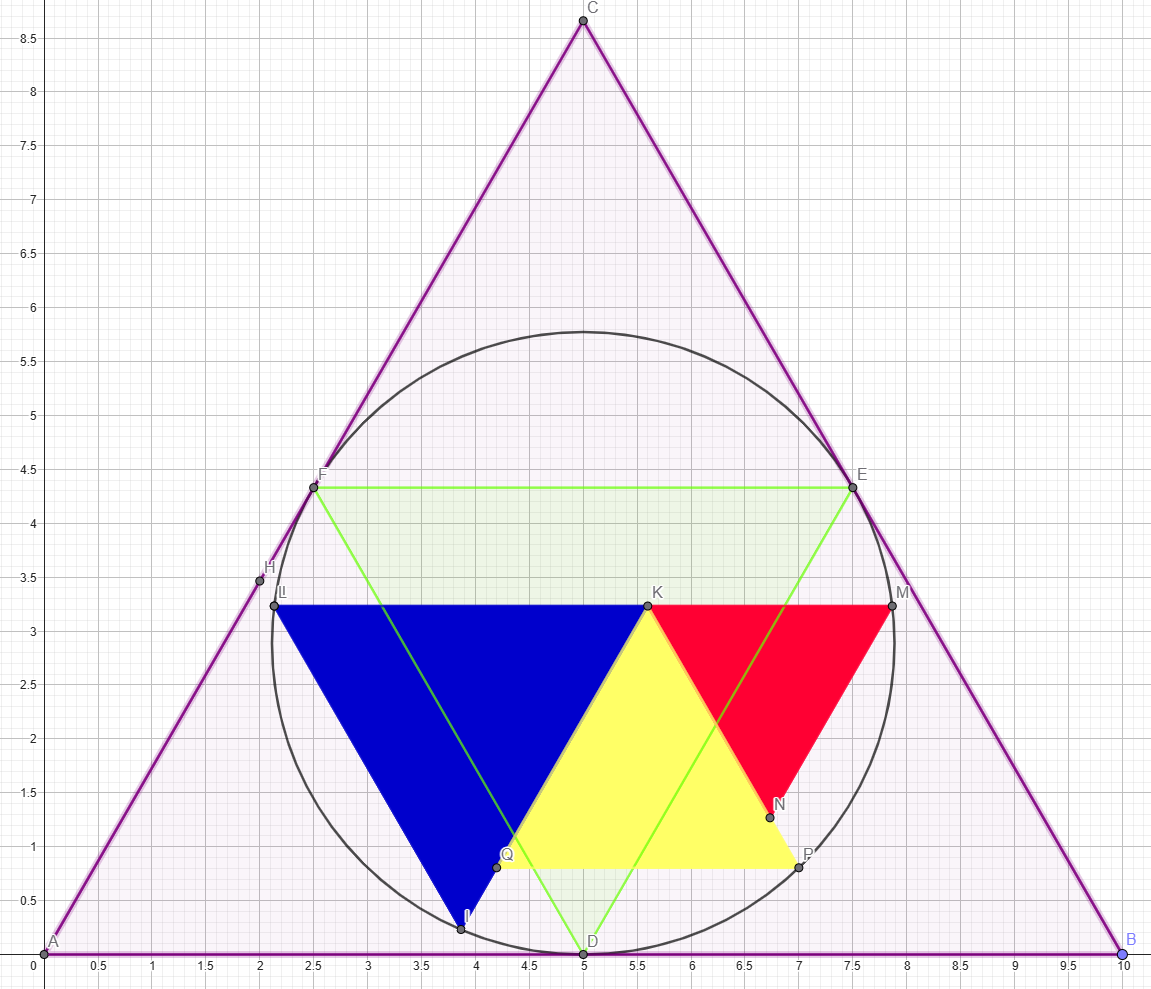
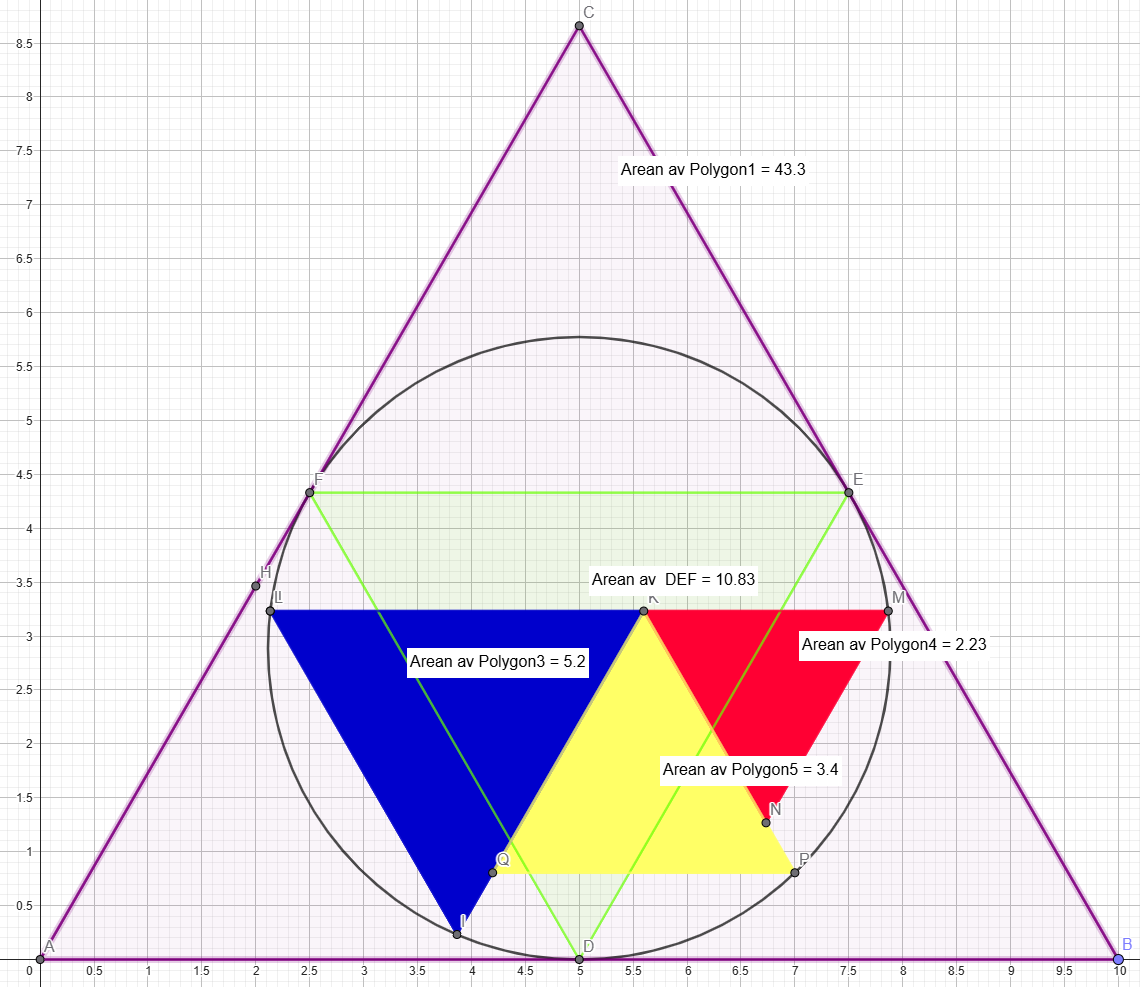
https://www.geogebra.org/classic/zpuwb8su
Trinity2 skrev:Jag försöker finna någon analytiskt angreppspunkt på att beskriva figuren geometriskt (koordinater m.m.) men finner ingen bra start. Har ni någon idé?
Jag tänkte att man utgår från 3 (små) trianglar enligt bild med sidorna s1, s2, och s3.
Första problemet är att finna cirkelns medelpunkt, M.
M_x = 1/2(s1+s3)
men vi kan sätta den till M_x=0 för enkelhetens skull.
Givet 3 punkter kan man finna cirkelns ekvation, men hur kommer man vidare, på ett bra sätt och finner M?
Om vi säger att cirkelns radie är 1, så kan vi sätta den blå triangelns sida som a och konstruera den. Sedan förlänger vi den övre sidan åt höger till cirkeln och får den röda triangelns övre sida. Den gula triangeln stoppar vi in sedan mellan de båda andra så att den tangerar cirkeln.
Laguna skrev:Trinity2 skrev:Jag försöker finna någon analytiskt angreppspunkt på att beskriva figuren geometriskt (koordinater m.m.) men finner ingen bra start. Har ni någon idé?
Jag tänkte att man utgår från 3 (små) trianglar enligt bild med sidorna s1, s2, och s3.
Första problemet är att finna cirkelns medelpunkt, M.
M_x = 1/2(s1+s3)
men vi kan sätta den till M_x=0 för enkelhetens skull.
Givet 3 punkter kan man finna cirkelns ekvation, men hur kommer man vidare, på ett bra sätt och finner M?
Om vi säger att cirkelns radie är 1, så kan vi sätta den blå triangelns sida som a och konstruera den. Sedan förlänger vi den övre sidan åt höger till cirkeln och får den röda triangelns övre sida. Den gula triangeln stoppar vi in sedan mellan de båda andra så att den tangerar cirkeln.
Denna (och #7): Du är onekligen mycket skicklig. Det är intressant. Jag skall se om jag kan modellera figuren med ett par parametrar i TikZ givet dina råd. Tack!
 Längden på den blå triangelns sida kan väljas från cirkelradien (t v) till ("nästan") halva den stora triangelns sida (t h). Då varierar förhållandet från 1/8 till 1/4. Hur var den ursprungliga "kluringen" exakt formulerad?
Längden på den blå triangelns sida kan väljas från cirkelradien (t v) till ("nästan") halva den stora triangelns sida (t h). Då varierar förhållandet från 1/8 till 1/4. Hur var den ursprungliga "kluringen" exakt formulerad?
hansa skrev:
Längden på den blå triangelns sida kan väljas från cirkelradien (t v) till ("nästan") halva den stora triangelns sida (t h). Då varierar förhållandet från 1/8 till 1/4. Hur var den ursprungliga "kluringen" exakt formulerad?
Grejen är att förhållandet inte varierar. Det spelar ingen roll vilken exakt längd man väljer på den blå triangeln, se GeoGebra (det går att dra i den markerade skärningspunkten mellan cirkeln och den svarta vågräta linjen)
Här kommer en lösning där man klarar sig med klassisk geometri där formlerna baseras på sidlängder/vinklar/radier/areor utan att använda sig av koordinater i ett koordinatsystem.
Visa spoiler
Antag att cirkeln har radien . Då har den stora triangeln sidlängden och arean .
Beteckna sidlängderna för den blåa, röda, respektive gula triangeln med , , respektive .
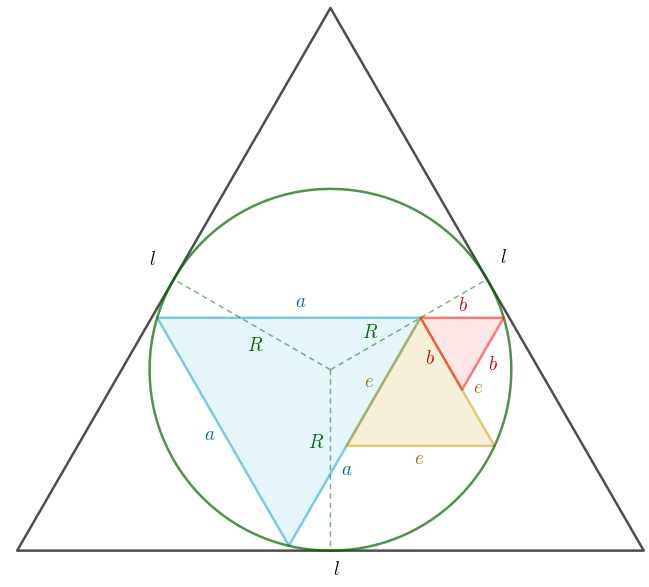
Man börjar på liknande sätt som i #7, d.v.s. spegla/rotera både den röda och den gula triangeln, så att man får följande:
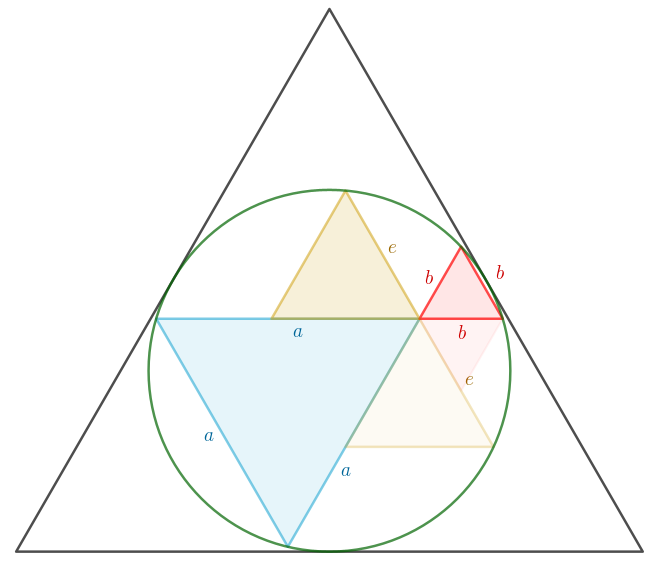
Enligt kordasatsen är . Den gula triangeln har därmed arean .
Inget mer kommer att göras med den gula triangeln, så jag döljer den i nästa figuren. Bilda ett likbent parallelltrapets genom att lägga till sträckor som kopplar ihop hörnen av den blåa med den roterade röda triangeln. (Dessa sträckor har sidlängden .)
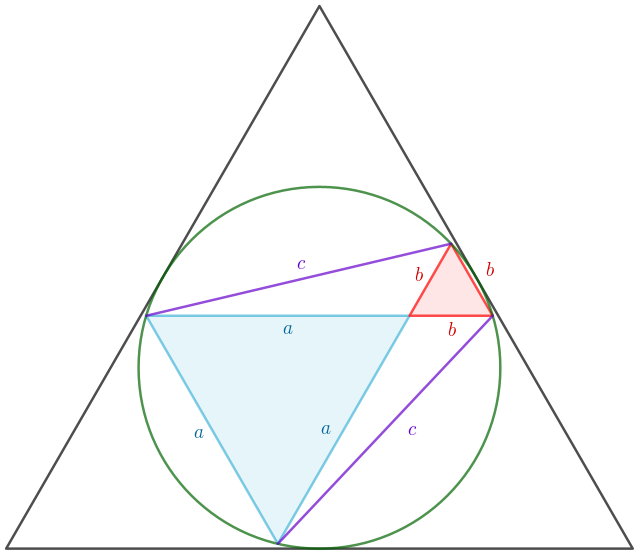
Enligt Ptolemaios sats är , vilket medför att .
Den gröna cirkeln har radien sedan början och denna cirkel är omskriven till det likbenta parallelltrapetset, så radien kan också beräknas enligt formeln . Genom att sätta in , så får man sambandet .
Nu har man alla ingredienser för att beräkna summan av de färgade trianglarnas areor:
- (liksidig triangel med sidlängden )
- (liksidig triangel med sidlängden )
- (togs fram ovan)
.
Det sökta förhållandet blir då:



