Kluring
I denna
https://www.pluggakuten.se/trad/kluring-rotekvation/
gjordes en listig substitution. Kan något liknande göras här?
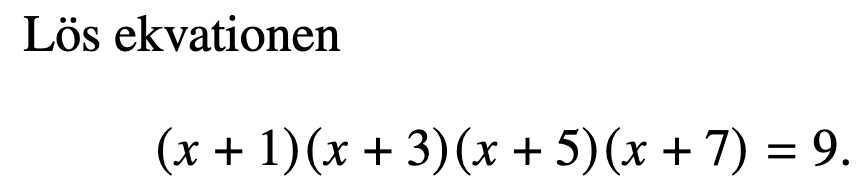
På nätet påstår de att det är ett problem från intagningsprovet på Harvard runt sent 1800-tal. Det har jag nog lite svårt att tro då nedanstående problem är betydligt mera "rakt" fram, även om det är från MIT,

Låt t=x+4, ger en fin lösning.
Låt t=x+4: (x+1)(x+3)(x+5)(x+7) = (t-3)(t-1)(t+1)(t+3) = (t^2-9)(t^2-1) = t^4-10t^2+9 = 9 -> t^4-10t^2 = 0 -> t^2(t^2-10) = 0 ->
t1^2 = 0 -> x+4=0
t2^2 =-> x+4=
vimärbäst skrev:Låt t=x+4: (x+1)(x+3)(x+5)(x+7) = (t-3)(t-1)(t+1)(t+3) = (t^2-9)(t^2-1) = t^4-10t^2+9 = 9 -> t^4-10t^2 = 0 -> t^2(t^2-10) = 0 ->
t1^2 = 0 -> x+4=0
t2^2 =-> x+4=
En bra lösning! Man kan även sätta u=t^2-5 i mellansteget, men det är en smaksak.


