Kluringar
Beräkna
Summan är divergent.
n-summan blir 1/(1 - 1/m) - 1 = 1/(m - 1).
Kvar blir då summa av 1/m från m = 1 till oändligheten, vilket är en känd divergent summa.
Nej då, summan konvergerar. Du har inte beräknat n-summan korrekt, du har att
men lägg märke till att n startar på 2 i summan Henrik skrev, inte 0.
Tack, jag missade en term. n-summan blir 1/(m(m - 1) så m-summan konvergerar.
Den inre summan är bara en geometrisk progression:
Vidare har vi att
Bra, din tur.
Låt
.
där och är positiva heltal. Bestäm .
Har du formulerat problemet rätt Lirim.K? Det inte ut som p + q är unik bestämt från endast det där.
Gissar att p & q är heltal? Givet differensen mellan två godtyckliga positiva tal känns det svårt att beräkna summan av deras kvadrater...
Jo det ska gå, ser inget misstag i uttrycket. Ber om ursäkt för att jag missade skriva med att p och q var heltal. Det är så klart viktigt. Börja t.ex. att multiplicera VL med konjugatet av det som står under det största rottecknet:
@Harald: Ja det stämmer! Editerar uppgiften med att lägga till denna information.
Anta
Det ger lösningen p=1006, q=1005. Saknar dock resonemang för att lösningen är unik.
Helt rätt harald. Vad menar du med att du saknar resonemang för unik lösning? Den lösning du angivit är den enda heltalslösningen (även enda reella) som ekvationssystemet kan ha.
Jo, den är unik för ekvationssytemet, men uppdelningen i de två ekvationerna drog jag ur hatten. Hur vet jag att
inte har några heltalslösningar för något nollskilt c?
Du har att
Där c är något heltal, kvadrerar man andra ekvationen så får man
och eftersom HL måste vara ett heltal här, så har man inte så mycket annat val än att c = 0.
Såklart, tack
Bra! Din tur, harald.
Hade en lite annorlunda lösning av Lirims problem som jag bara gärna injicerar här lite emellan eftersom den rent
Tricket är att skapa två algebraiska ekvationer för samma tal och sedan jämföra deras koefficienter för att finna . Låt oss beteckna vilket alltså är även är . Genom potenser och omflyttningar av dessa två uttryck får vi två ekvationer detta tal måste tillfredställa.
Först
och sen från
ser vi spontant att är multiplikativa inversen till ett tal som tillfredställer ekvationen
Multiplicera denna ekvation med , använd , och flytta runt lite.
Error converting from LaTeX to MathML.
Vi har alltså de två ekvivalenta ekvationera
.
och från koefficienternas unicitet följer alltså
Vill vi ha de faktiska talen löser vi ekvationsystemen
Mycket snyggt! Alla lösningsförslag är väldigt välkomna. Är du SeriousSquid från gamla PA?
harald, Stokastiskt eller Serious får slänga in ett nytt problem. Jag sitter i en lång bilfärd med gratis 4G ner till Italien och är mycket uttråkad. Mata mig med problem.
OK, ny uppgift:
Två cirklar tangerar varandra i P, och en linje l i A respektive B. linjen mellan A och P skär den andra cirkeln i C. Visa att CB är vinkelrät mot l.
Om man drar diametrar för båda cirklarna som går genom punkterna A och B, som i bilden. Sedan drar man linjen som går genom C och P, denna linje skär linjen SA i punkten Q, utifrån de likformiga trianglarna som bilda så får man att |SQ| = |SP|, vilket innebär att Q = A. Så alltså är AP samma linje som PC varav det följer att CB är vinkelrät mot linjen l.
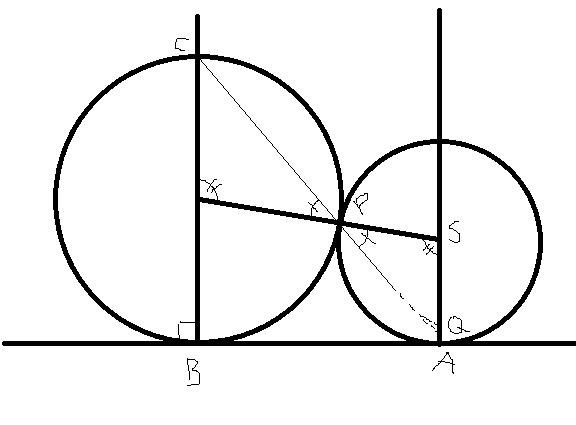
@SeriousCephalopod Jag tror inte din lösning stämmer tyvärr. För det första verkar du aldrig utnyttja att p och q är heltal, vilket man måste för att lösa uppgiften. Jag har inte tänkt igenom detta i detalj, men det känns inte riktigt rätt att säga att du kan jämföra polynomens koefficienter. Notera att x är ett fixt tal i din lösning, så det är inte två polynom.
@Stokastiskt Det är möjligt stt det finns en defekt i resonemanget men det stämmer inte att jag inte utnyttjar att pq är heltal. Polynomen förutsätts vara de "minsta" polynomen med heltaskoefficienter för vilka x är en lösning. Uniciteten i koefficienterna följer sedan från att sådana polynom måste vara unika. Att jag inte visar att de verkligen är de minsta och att min formella kunskap om minimala polynom är marginell är dock sant.
Men ska jag vara ärlig är det i grunden en fysikers pragmatism. Faller något ut från symbolerna är det förmodligen sant.
@Lirim Ja. Densamma. Sidan buggade när jag skulle migrera kontot så struntade i det.
@SeriousCephalopod Aha, jag tror jag poletten för ner för mig. Snygg lösning :)
@Stokastisk: Jag är nog inte riktigt med. C är ju definierad utifrån att den ligger på linjen AP, men om jag tolkar dig rätt så definierar du C som den diametralt motsatta punkten till B?
@haraldfreij: Ja det stämmer bra att jag definierar det annorlunda. Jag insåg efter att jag postade att jag var lite otydlig på den punkten. Säg att jag låter den punkten vara C', jag drar linjen genom C' och P och visar att denna linje skär A. Därav följer det att linjen genom A och P kommer skära genom C' och därmed är C' = C.
Absolut, då är vi hemma. Din tur.
Låt f vara en funktion med kontinuerlig derivata på [0, 1] och med egenskapen att , samt att det gäller att f(0) = 0. Bevis följande olikhet
Sambandet visas medelst Riemannintegraldefinitionen.
är underförstått i summationerna.
Då gäller att:
.
Sambandet gäller efter f(x) är i intervallet [0,1] p.g.a. begränsningen av derivatan.
Det där ser ut att kunna fungera, men första olikheten känns inte som du motiverat?
Stokastisk skrev :Det där ser ut att kunna fungera, men första olikheten känns inte som du motiverat?
Bra poäng Stokastisk! Det steget behöver motiveras. Är på resande fot nu så låter det vara "up for grabs" för alla att motivera det steget och därmed formulera nästa problem i tråden.
Jag är klart tveksam till om det steget är sant över huvud taget. Ta t.ex.
Då får vi
Ja det har du nog rätt i harald. Steget skulle ju exempelvis innebära att
vilket man kan verifiera att det inte är sant. Jag kan dock försäkra om att olikheten jag skrivit stämmer.
Jag slänger in en liten hint. Om man vill visa att g(x) >= 0, x > 0, så kan man visa att g(0) = 0 och g(x) är växande, samma idé är användbar för att bevisa den olikhet jag skrev.
Slänger in en till hint, undersök följande funktion.
Det känns som att det är något i stil med att:
g(0) = 0
Samt:
g'(x) = 2(F(x)-F(0))*f(x) -... >= 0
man ska visa.
Det är korrekt tomast80, för om man lyckas visa det för x <= 1 så följer ju olikheten g(1) >= 0 som är den man ska visa.
Hej!
Vad tror du om följande förslag Stokastisk?
Det gäller att visa olikheten
Eftersom på det öppna intervallet (0,1) så är kvoten
för alla 0<x<1,
och det följer att integralen är uppåt begränsad av
Medelvärdessatsen ger att för varje gäller det att
för något
Antagandet att för alla medför att
för alla
Detta betyder att integralen
är uppåt begränsad av integralen
Albiki
Tyvärr så är nog inte olikheten
sann. Säg att f(x) = x, då har vi att integralen i nämnaren är 1/2 och täljaren är x, så olikheten säger att vilket inte är sant då x > 1/2.
Hej!
Det har du rätt i.
Mitt resonemang bör gå att rädda om det gäller att
för alla
Albiki
Hej!
Jag inser att denna olikhet ska gälla för alla funktioner som uppfyller problemets villkor. Eftersom funktionen (där ) uppfyller problemets villkor, och funktionen bryter mot den önskade olikheten, så drar jag slutsatsen att olikheten inte gäller för alla funktioner som uppfyller problemets villkor.
Tillbaka till ritbordet!
Albiki
Stokastisk skrev :Låt f vara en funktion med kontinuerlig derivata på [0, 1] och med egenskapen att , samt att det gäller att f(0) = 0. Bevis följande olikhet

Hej Olba12.
Låt , vi vet då att
Samtidigt gäller det att
Det gäller med andra ord att . Så beviset håller tyvärr inte.
Stokastisk skrev :Hej Olba12.
Låt , vi vet då att
Samtidigt gäller det att
Det gäller med andra ord att . Så beviset håller tyvärr inte.
Ahh mycket riktigt!
Frågan är då om det håller att det skulle innebär att
Eller så medelvärdessatsen inte hjälpbar här.
Jag tipsa om att du inte behöver använda medelvärdessatsen. Nu har du problemet att du vill visa att g'(x) >= 0, så ungefär samma idé man försöker utnyttja för att visa att g(x) >= 0 kanske är användbar för att visa att g'(x) >= 0?
Ok.
g'(x) = 2(F(x)-F(0))*f(x) - f(x)^3
g'(0) = 0
g''(x) = 2*f(x)*f'(x) + 2(F(x)-F(0))*f'(x) - 3f(x)^2*f'(x)
Man borde kunna visa att g''(x) >= 0.
Att bara derivera g' rakt av är nog inte bästa sättet att lösa det på. Men att derivera något uttryck relaterat till g' är mer rimligt, om man deriverar rätt uttryck så är det uppenbart utifrån premisserna i uppgiften att olikheten stämmer.
Observera att och antyder att, för , så gäller det att
.
Bilda funktionen
på intervallet . Eftersom så räcker det med att visa att är en växande funktion, då är och olikheten som ska visas håller. Genom derivation så erhålles
.
Beteckna funktionen inom parentesen ovan med , så gäller det att växer på intervallet omm . Eftersom så gäller det att . Villkoren och medför att
Detta visar att växer och att Detta medför i sin tur att växer och vi är klara.
Snyggt Lirim! Det där stämmer. Din tur.
Jag hoppas att ingen motsätter sig att jag lägger upp ett litet problem i Lirims frånvaro.
A flag token has a blue side and a yellow side. A positive integer less than or
equal to 100 is written on each side of every token (the numbers on the two sides
may be different). Two flag tokens are identical if the numbers on the blue sides of
both tokens are equal, and the numbers on the yellow sides of both tokens are equal.
Two flag tokens are called compatible if the numbers on the blue sides of both tokens
are equal, or the numbers on the yellow sides of both tokens are equal. Given 2559
flag tokens such that there is no identical pair among them, show that at least one
of them is compatible with at least 50 other among them.
Istället för flaggor så kan vi se det som att vi har placerat ut brickor i ett 100x100 rutnät. Om en bricka är placerat på position (2, 3) i rutnätet så motsvarar det en flagga med en 2:a på blå sidan och en 3:a på gula sidan. Så man har alltså exakt 2559 rutor i nätet där det är brickor placerade.
Låt nu vara antalet brickor placerade på kolumn i, och vara antalet brickor placerade på rad i. Låt nu
Man kan då se att
Detta eftersom kommer finnas som term i exakt stycken , och liknande resonemang för . Nu följer det av Cauchy-Schwarz att
och liknande olikhet för . Så man har alltså att
Där den sista likheten följer av att summorna bara räknar antalet brickor som finns på rutnätet. Alltså vet vi att
Eftersom det är exakt 2559 stycken som kan vara nollskilda och att , så följer det att vi måste kunna finna något par (i, j) så att . Detta innebär alltså att brickan på positionen (i, j) måste ha stycken brickor som ligger på samma rad eller kolumn som den själv (där -2 kommer in eftersom brickan (i, j) räknas två gånger i summa ).
Det är exakt detta vi ville visa, eftersom de brickor som ligger på samma rad/kolumn representerar de flaggor som är kompatibla med flaggan som representeras av brickan (i, j).
Japp! Nästan samma som min lösning men jag använde Jensen i stället för Cauchy. Din tur mannen!
Om vi har punkter i planet. Visa att det finns tre punkter, A, B, C sådana att .
Jag förstår inte uppgiften. Ska man visa att vinkeln vid B alltid är mindre än eller lika med pi/n, där n också är antalet punkter i triangeln? Hänger inte med.
Jag tolkar det som att vi har n godtyckliga punkter i xy-planet. Sen tar du de tre punkter bland dessa: A, B och C mellan vilken vinkeln är minimal. Då är den maximalt π/n stor. Tänk en triangel (n=3): det finns alltid minst en vinkel som är <= π/3 = 60 grader.
tomast80 har tolkat problemet korrekt.
Intressant uppgift. Jag skulle vilja be om att få en hint för denna.
Första steget i lösningen skulle vara att vi väljer en av de punkter i planet som ligger längst ned och kallar denna för O. Sedan fortsätter man resonera utifrån vad som måste gälla för vinklarna relaterade till O.
Om alla n punkterna ligger på en och samma linje är väl vinkeln dem emellan π > π/n? Är det en otillåten samling punkter?
Om punkterna ligger på linjen i ordningen B - A - C så skulle jag säga att .
Stokastisk skrev :Om punkterna ligger på linjen i ordningen B - A - C så skulle jag säga att .
Bra poäng! Inget säger ju att man måste välja närliggande punkter!
- Rita konvexa höljet av punkterna. Vinkeln vid något hörn är som mest pi*(n-2)/n. Dra linjer till alla n-1 andra punnkter. Det blir n-2 vinklar. Medelvinkeln är alltså som mest (pi*(n-2)/n)/(n-2)=pi/n...
Japp, det där stämmer, snygg lösning. Din tur.





