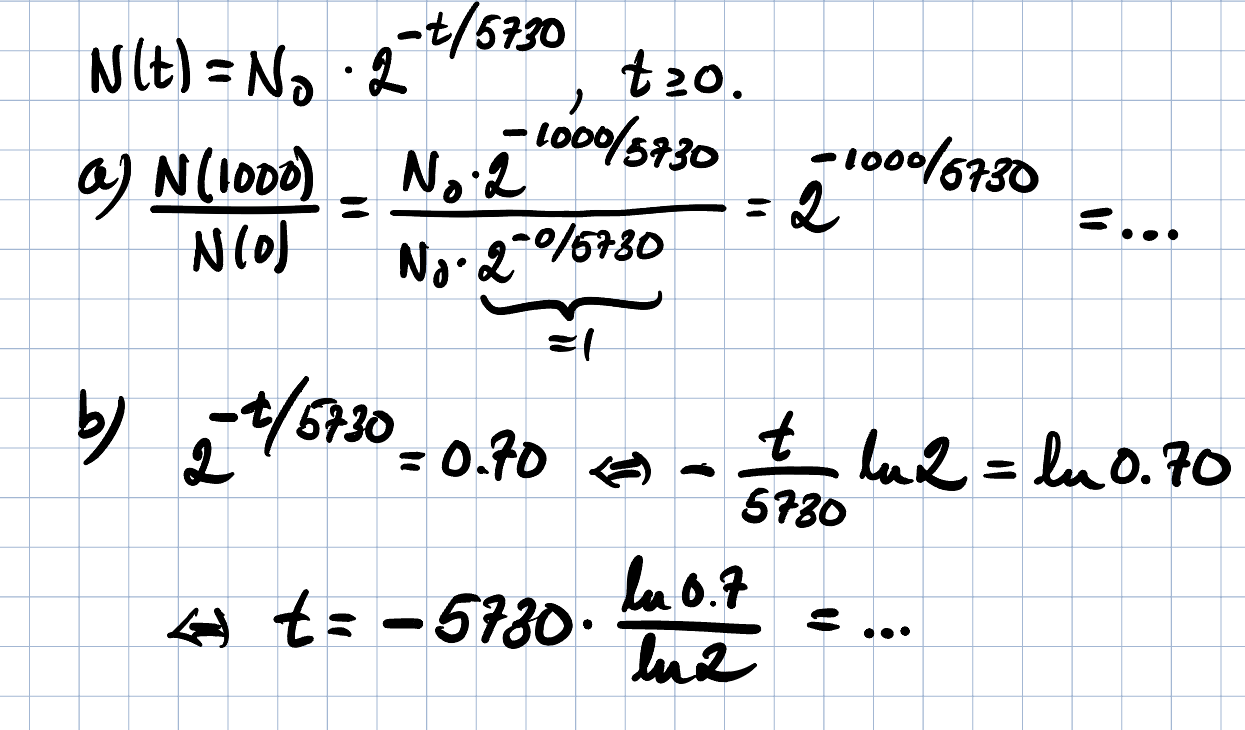Kol-14 halveringstid
Hej!
hade behövt lite hjälp med följande fråga:
 det jag har kunnat komma på är att man kan ersätta t och T e exponenten med 1000 och 5730, men jag vet inte hur jag ska gå tillväga därefter eftersom att man inte vet hur mycket kol-14 det finns skelettet från början.
det jag har kunnat komma på är att man kan ersätta t och T e exponenten med 1000 och 5730, men jag vet inte hur jag ska gå tillväga därefter eftersom att man inte vet hur mycket kol-14 det finns skelettet från början.
ska man alltså räkna ut vad N0 Blir först och sedan stoppa in det värdet i ekvationen? Får det?
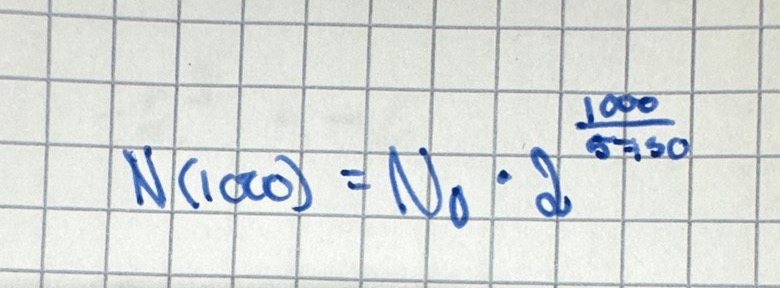
Tacksam för all hjälp!
Du behöver (och kan) inte veta hur mycket kol-14 som fanns från början.
Säg istället att det fanns 100% initialt, alltså sätt N0=1.
Då kommer N(1000) att vara hur mycket som är kvar av 100% efter 1000 år.
tack! Jag lyckades lösa a-uppgiften, den var mycket lättare är jag trodde när jag väl kom fram till vilken ekvation jag skulle lösa.
PÅ b-uppgiften blir det dock lite svårare för mig.
Om vi säger att 2-t/5730 = 0,7 så kan man använda sig av en potenslag så vi får 1/(2^t/5730) i V.L Efter att ha följt balansmetoden kom jag fram till att 10=7*2^(t/5730)
Det svåra för mig är att få ut t från exponenten, för man vill ju få uttrycket med exponenten ensam i ena ledet. Det jag kan tänka på är att använda inversen hade kunnat vara ett möjligt steg på vägen, men verabeln blir fortfarande kvar i exponenten, så det är inte till så stor hjälp ändå.
Jag lyckades lösa uppgiften mha geogebra, skrev in exponentialfunktionen 2-t/5730 och la därefter till att y=0,7. Skärningspunkten angav då hur gammalt fyndet var. Men Jag är fortfarande nyfiken på hur man hade kunnat lösa denna uppgift utan sådana hjälpmedel.
Det kan vara så att denna typ av ekvationer kommer först i Ma2 och de menar att man skall använda GGB och då har du gjort rätt. Senare kommer du att lära dig att lösa dessa enkelt.
oki, tack snälla för din hjälp!