Kombinationer....
Hej, har precis börjat med kombinatorik och gått igenom kombinationer respektive permutationer. Tycker det är svårt. Sitter med en riktig klurig uppgift nu.
Frågan:
Du har 17 olika elever.
De ska delas in i följande grupper:
-
7 grupper med 2 elever i varje
-
1 grupp med 3 elever
På hur många olika sätt kan de 17 eleverna delas in på detta sätt?
Min idé:
Först gör jag 8 par av de 16 första eleverna, och sedan låter jag den 17:e eleven gå till någon av grupperna:
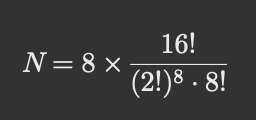
Dvs. det finns 8 sätt att välja den sista eleven i en grupp med 2 och de 16 övriga eleverna är redan i grupper om 2.
Facit:
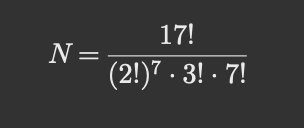
Kombinatorik är så fruktansvärt svårt...Många liknande uppgifter och jag förstår ingenting. Är det möjligt om någon kan förklara denna uppgift och ge tips på hur man ska tänka kring generellt svårare uppgifter inom området?
17 elever ska delas in i 7 [par] och 1 [trio],
dvs i 8 grupper, varav 7 [par] och 1 [trio].
Det kan ske på 17! / ((2!7 ·3!) olika sätt,
dvs 17! / (27 · 6).
Kolla begreppet multinomialkoefficient,
en generalisering av binomialkoefficient.
Jag förstår inte den sista faktorn i nämnaren i facit, 7! .
Har jag missat något i uppgiften eller är det fel i facit?
Så här är min tolkning av det, och det är inte så enkelt att fästa ord på detta då det är abstrakt. Kanske någon mera lärd kan förmedla ett mera kortfattat, rigoröst och klarare resonemang.
För det första kan det inte sägas tillr. många gånger: Kombinatorik är svårt. Det handlar om att tänka "rätt" direkt och inte "snöa in på ett tankesätt" som leder en på fel väg. Vi har alla(!) snöat in på fel saker, du är inte ensam.
Om vi tittar på uppgiften är den "dubbeldefinierad" i frågeställningen. Om vi väljer 7 grupper med 2 elever får vi automatiskt kvar 3 elever varpå den gruppen är "auto-genererad" av vårt första 7-faldiga val. Den gruppen är alltså ur valsynpunkt inte primär. Den uppkommer av sig själv. Vi kan säga att "de resterande 3 som inte väljs" blir en grupp av sig själva genom vår aktiva process att välja de 7 grupperna. Alltså är det inte intressant att betrakta dessa i urvalsprocessen.
Fullt fokus på de 7 grupperna alltså. Vi återkommer till de 3 sista senare, men just nu är de perifera och ointressanta.
Sedan börjar vi med betrakta hur det blir när ordningen är viktig.
Säg att vi har följande "grundordning" av 7 st. 2-elevsgrupper
A1A2 B1B2 C1C2 D1D2 E1E2 F1F2 G1G2
Vi kan permutera dessa grupper på 7! olika sätt.
Dessutom, inom varje grupp kan vi permutera de 2 medlemmarna på 2!=2 olika sätt. Eftersom det är 7 grupper blir det nu 7! * 2^7 olika sätt
Så långt allt väl. Då har vi bara kvar "resten". Denna "auto-genererade" grupp kan permuteras på 3! olika sätt
Vi har nu 7! * 2^7 * 3! olika ORDNADE val där vi inkluderat den resterande 3-gruppen också. (*)
Om vi betraktar alla elever som unika individer (ej gruppindelade) kan dessa ställas upp på 17! ORDNADE sätt.
För att få det OORDNADE antalet skall vi dividera detta tal, 17!, med (*) och får det önskade svaret.
Vän av ordning frågar sig nu: ”Varför betraktar vi inte var 3-gruppen hamnar i sekvensen av 2-lag?” Det beror på att 3-gruppen är en ”biprodukt” av det primära urvalet. 3-gruppen blir automatiskt skapad SIST som en rest av den primära selektionen. Vi kan då INTE börja stoppa in den här och där i sekvensen av 2-grupper. Valet av de 3 är INTE ett AKTIVT val, utan ett PASSIVT val. Detta sker när en ”vald grupp” egentligen är en biprodukt av en annat, primärt och aktivt urval.
Och så till din ansats:
Det är inte så dumt tänkt, men vi kommer få identiska uppsättningar som överlappar varandra. Säg att en ordnad uppställning är
A1A2 B1B2 C1C2 D1D2 E1E2 F1F3 G1G2 H1H2
Detta är 8*2=16 elever och vi skall nu placera ut den sista eleven (=X)
Säg att vi sätter denne sist i 1:a gruppen
A1A2X B1B2 C1C2 D1D2 E1E2 F1F3 G1G2 H1H2
Detta är exakt samma "17-uppställning" som att sätta denne först i 2:a gruppen;
A1A2 XB1B2 C1C2 D1D2 E1E2 F1F3 G1G2 H1H2
Vi har alltså liknande "17-uppställningar" av elever och vi "dubbelräknar" därmed dessa.
Notera att den ensamma eleven är INTE en biprodukt som ovan. Visserligen ”blir denne över” efter den primära selektionen, men iochmed att vi nu börjar ”stoppa in denne” här och var i 2-grupperna så påverkar vi deras konstellation/tidigare urval och det är inte det samma som den ”biprodukts-grupp” vi hade ovan.
I vissa fall KAN man reda ut dessa dubbelräkningar (genom att subtrahera andra kombinatoriska värden) men om det är för komplext (som här, även om man säkert skulle kunna reda upp det efter lite tänkande) indikerar det att man är på fel väg, även om det verkade smart från början. (Detta är en klassisk känsla av obehag som nästan alla får vid kombinatorik - det verkar smart, men skapar svårhanterliga problem.)
Tack för ett otroligt utvecklat och förstående svar. Tack!
Anonym_15 skrev:Tack för ett otroligt utvecklat och förstående svar. Tack!
Utmärkt att det kunde bringa någon form av klarhet i kombinatorikens dunkla vatten.
Undrar däremot en sak. Du säger här att detta ger samma uppsättning: A1A2X B1B2.. som A1A2 XB1B2... men "x" eleven ingår ju i olika grupper då, eller har jag missat något?
Anonym_15 skrev:Undrar däremot en sak. Du säger här att detta ger samma uppsättning: A1A2X B1B2.. som A1A2 XB1B2... men "x" eleven ingår ju i olika grupper då, eller har jag missat något?
Kruxet här är att vi visserligen väljer grupper, men ställer upp dem på en rad och "jämför" de med de 17! olika raderna som kan skapas när det är ORDNAD ordning.
17!-uppställningen har inga grupper, den är gränslös, och när vi tar bort "gränserna" i våra urval, så sammanfaller vissa urval, som t.ex.
A1A2X | B1B2 ....
blir gränslöst
A1A2XB1B2 ....
men
A1A2 | XB1B2 ....
blir också samma sak, gränslöst.
Arktos skrev:17 elever ska delas in i 7 [par] och 1 [trio],
dvs i 8 grupper, varav 7 [par] och 1 [trio].
Det kan ske på 17! / ((2!7 ·3!) olika sätt,
dvs 17! / (27 · 6).Kolla begreppet multinomialkoefficient,
en generalisering av binomialkoefficient.Jag förstår inte den sista faktorn i nämnaren i facit, 7! .
Har jag missat något i uppgiften eller är det fel i facit?
Tack Trinity!
Jag har uppenbarligen missförstått innebörden av en multinomialkoefficient, dvs hur den ska tolkas. Det blir att gå tillbaka till grunderna och börja om från början. Detta är både tankemässigt knepigt och svårt att uttrycka i ord. Du gör ett utmärkt försök, även om jag finner det svårt att följa, så som det ofta kan vara i kombinatoriska problem.
Själv tyckte jag uppgiften var som gjord för en multinomialkoefficient och tänkte inte mer på saken. Nu får jag gå på jakt i kurslitteraturen för matematisk statistik. Lära om!
@Anonym_15
Vilken kursbok använder du?
Arktos skrev:Arktos skrev:17 elever ska delas in i 7 [par] och 1 [trio],
dvs i 8 grupper, varav 7 [par] och 1 [trio].
Det kan ske på 17! / ((2!7 ·3!) olika sätt,
dvs 17! / (27 · 6).Kolla begreppet multinomialkoefficient,
en generalisering av binomialkoefficient.Jag förstår inte den sista faktorn i nämnaren i facit, 7! .
Har jag missat något i uppgiften eller är det fel i facit?Tack Trinity!
Jag har uppenbarligen missförstått innebörden av en multinomialkoefficient, dvs hur den ska tolkas. Det blir att gå tillbaka till grunderna och börja om från början. Detta är både tankemässigt knepigt och svårt att uttrycka i ord. Du gör ett utmärkt försök, även om jag finner det svårt att följa, så som det ofta kan vara i kombinatoriska problem.
Själv tyckte jag uppgiften var som gjord för en multinomialkoefficient och tänkte inte mer på saken. Nu får jag gå på jakt i kurslitteraturen för matematisk statistik. Lära om!
@Anonym_15
Vilken kursbok använder du?
Det är mycket lätt att gå vilse. Det har man gjort MÅNGA gånger själv.
En modern pedagog hade säkert gjort en fin video, men det är bortom min kunskap :) Kanske uppgiften finns på YouTube?
Jag googlade fram filmen, men har inte sett den. Jonas brukar dock hålla hög nivå, så den är säkert sevärd:
Matematik 5. Problemlösning kombinationer: Dela elever i grupper.
Uppdatering: Nu har jag kikat. Bra förklaring!
sictransit skrev:Jag googlade fram filmen, men har inte sett den. Jonas brukar dock hålla hög nivå, så den är säkert sevärd:
Matematik 5. Problemlösning kombinationer: Dela elever i grupper.
Uppdatering: Nu har jag kikat. Bra förklaring!
Ingen bra uppgift. Den rör till det för eleverna som säkerligen har gjort 50-11 uppgifter tidigare där man "permuterar 8!". Jag ser inte poängen att stöka till det i huvudet på dem.
Han är väldigt animerad. För animerad för mig.
sictransit skrev:Jag googlade fram filmen, men har inte sett den. Jonas brukar dock hålla hög nivå, så den är säkert sevärd:
Matematik 5. Problemlösning kombinationer: Dela elever i grupper.
Uppdatering: Nu har jag kikat. Bra förklaring!
Jag såg också videon men tyckte den var lite vilseledande....Tänkte på om det bara fanns detta enda sättet att lösa uppgiften på eller inte. Kan också vara så att den läraren inte gick igenom grunderna särskilt tydligt liksom Trinity2 gjorde.
Arktos skrev:Arktos skrev:17 elever ska delas in i 7 [par] och 1 [trio],
dvs i 8 grupper, varav 7 [par] och 1 [trio].
Det kan ske på 17! / ((2!7 ·3!) olika sätt,
dvs 17! / (27 · 6).Kolla begreppet multinomialkoefficient,
en generalisering av binomialkoefficient.Jag förstår inte den sista faktorn i nämnaren i facit, 7! .
Har jag missat något i uppgiften eller är det fel i facit?Tack Trinity!
Jag har uppenbarligen missförstått innebörden av en multinomialkoefficient, dvs hur den ska tolkas. Det blir att gå tillbaka till grunderna och börja om från början. Detta är både tankemässigt knepigt och svårt att uttrycka i ord. Du gör ett utmärkt försök, även om jag finner det svårt att följa, så som det ofta kan vara i kombinatoriska problem.
Själv tyckte jag uppgiften var som gjord för en multinomialkoefficient och tänkte inte mer på saken. Nu får jag gå på jakt i kurslitteraturen för matematisk statistik. Lära om!
@Anonym_15
Vilken kursbok använder du?

Denna!
Trinity2 skrev:Anonym_15 skrev:Undrar däremot en sak. Du säger här att detta ger samma uppsättning: A1A2X B1B2.. som A1A2 XB1B2... men "x" eleven ingår ju i olika grupper då, eller har jag missat något?
Kruxet här är att vi visserligen väljer grupper, men ställer upp dem på en rad och "jämför" de med de 17! olika raderna som kan skapas när det är ORDNAD ordning.
17!-uppställningen har inga grupper, den är gränslös, och när vi tar bort "gränserna" i våra urval, så sammanfaller vissa urval, som t.ex.
A1A2X | B1B2 ....
blir gränslöst
A1A2XB1B2 ....
men
A1A2 | XB1B2 ....
blir också samma sak, gränslöst.
Wow, det är verkligen svårt att tänka så här! Men tack igen. Ska försöka lösa uppgiften en gång själv (med din förklaring) och se hur det går.
Anonym_15 skrev:Arktos skrev:Arktos skrev:17 elever ska delas in i 7 [par] och 1 [trio],
dvs i 8 grupper, varav 7 [par] och 1 [trio].
Det kan ske på 17! / ((2!7 ·3!) olika sätt,
dvs 17! / (27 · 6).Kolla begreppet multinomialkoefficient,
en generalisering av binomialkoefficient.Jag förstår inte den sista faktorn i nämnaren i facit, 7! .
Har jag missat något i uppgiften eller är det fel i facit?Tack Trinity!
Jag har uppenbarligen missförstått innebörden av en multinomialkoefficient, dvs hur den ska tolkas. Det blir att gå tillbaka till grunderna och börja om från början. Detta är både tankemässigt knepigt och svårt att uttrycka i ord. Du gör ett utmärkt försök, även om jag finner det svårt att följa, så som det ofta kan vara i kombinatoriska problem.
Själv tyckte jag uppgiften var som gjord för en multinomialkoefficient och tänkte inte mer på saken. Nu får jag gå på jakt i kurslitteraturen för matematisk statistik. Lära om!
@Anonym_15
Vilken kursbok använder du?
Denna!
Aha!
Vilket uppg.nr?
Jag såg att de nu finns 7000. troligen ny läroplan, igen...
Som Trinity2 redan skrivit så är det lätt att man råkar slå slint då man jobbar med kombinatorik. Så här skulle jag förklara facits lösning:
Vi vill placera våra 17 elever på en rad, där det finns avgränsare som indikerar att vissa positioner indikerar att man är del av en viss grupp.
_ _ | _ _ | _ _ | _ _ | _ _ | _ _ | _ _ | _ _ _
Att placera 17 objekt på en rad kan göras på 17! vis. Emellertid så kommer vissa permutationer utgöra exakt samma lösning trots att eleverna inte står i exakt samma ordning. T.ex. är följande två ordningar hel ekvivalenta:
A B | C D | E F | G H | I J | K L | M N | O P Q
B A | D C | F E | H G | J I | L K | N M | P Q O
Det jag gjort är att byta den inbördes ordningen i de olika grupperna. Hur många sätt kan man göra detta på? En grupp på två kan ombildas genom att permuteras på 2! vis; en grupp på tre kan ombildas genom att permuteras på 3! vis. Med andra ord, om vi skriver att lösningen är 17! får vi 2!*2!*2!*2!*2!*2!*2!*3! gånger så många permutationer som det egentligen är, så vi får dividera med det.
Vidare så spelar ordningen vi placerar grupperna i ingen roll. Men i ovanstående beskrivning så säger vi att den spelar roll. Följande två permutationer betraktas som olika om vi inte gör någon justering:
A B | C D | E F | G H | I J | K L | M N | O P Q
I J | K L | M N | G H | A B | C D | E F | O P Q
Eftersom att vi har 7 stycken grupper om 2 så kan vi för en given permutation få en helt ekvivalent permutation genom att byta plats på innehållet i en av grupperna med innehållet i en annan av grupperna, och därmed få en permutation som vi för närvarande betraktar som en helt ny permutation trots att vi inte borde göra det. För att råda bot på det får vi dividera med 7!, eftersom det är så många sätt som vi kan placera innehållet i 7 grupper på.
Detta ger facits lösning.
Om vi sedan tittar på hur som du först försökte lösa uppgiften så är din lösning ganska nära facit. Det som skiljer sig åt är att din lösning multiplicerad med 17 och dividerad med 3 ger den riktiga lösningen. Jag kan härleda var detta kommer från. Du skriver att:
"Först gör jag 8 par av de 16 första eleverna, och sedan låter jag den 17:e eleven gå till någon av grupperna:"
Med den här premissen kommer elev nummer 17 alltid vara en del av gruppen med 3 deltagare. Du får inte med de fall då den eleven är i en grupp på bara 2. Med andra ord har det betydelse vilken elev som blir "elev nummer 17", så vi måste ta hänsyn till det valet. Vi gör detta genom att multiplicera med antalet vis som man kan välja ut 1 elev av 17 på, (17 över 1) vilket motsvarar en multiplikation med 17.
Sedan är det divisionen med 3:an. Antag att du valde ut eleven C som elev nummer 17 och sedan bildade grupperna: {[A B], [D E], [F G], [H I], [J K], [L M], [N O], [P Q]}, varpå C släntrade in i första gruppen och du fick permutationen: {[A B C], [D E], [F G], [H I], [J K], [L M], [N O], [P Q]}. Antag att du istället valde eleven A som elev nummer 17 och bildade grupperna {[B C], [D E], [F G], [H I], [J K], [L M], [N O], [P Q]} och A släntrade in i första gruppen och du fick permutationen: {[A B C], [D E], [F G], [H I], [J K], [L M], [N O], [P Q]}. Antag att istället eleven B blev elev nummer 17 och du bildade grupperna {[A C], [D E], [F G], [H I], [J K], [L M], [N O], [P Q]} och B släntrade in i första gruppen och du fick permutationen: {[A B C], [D E], [F G], [H I], [J K], [L M], [N O], [P Q]}.
Vi har nu fått fram tre permutationer som din uträkning betraktar som unika trots att de inte är det. Och vi skulle kunnat göra samma sak med en godtycklig permutation av 8 grupper om två där elev nummer 17 släntrar in i en av grupperna; skapa samma permutation fast ersätt en av elev nummer 17:s framtida grupp med elev nummer 17 och dess ersättare som den nya elev nummer 17 och du får att vi räknat samma permutation flera gånger. För att råda bot på detta fel får vi dividera med 3. Precis som de gör i facit.
Tack! Jag undrar bara vart division med 3 kommer ifrån? Förstår inte riktigt. Den gruppen med 7 eleven kan väl ordnas på 3! olika sätt inom gruppen?
Jag har härlett var divisionen med 3 kommer i från i mitt förra inlägg. Den kommer från att om vi inte dividerar med tre så kommer de permutationer som blev identiska, där den enda skillnaden är vilken av eleverna i tre-gruppen som var ”elev nummer 17”, räknas som tre unika permutationer.
Om du undrar varför jag ville ha det till att en division med tre saknades så kan du jämföra din lösning med facit. Du dividerade med 2! åtta gånger; facit dividerade med 2! sju gånger och 3! en gång. Skillnaden är en multiplikation med 3.


