kombinatorik
Hej
jag har fastnat på en fråga jag vet inte hur jag ska tänka. hjälppppppp
Välkommen till Pluggakuten!
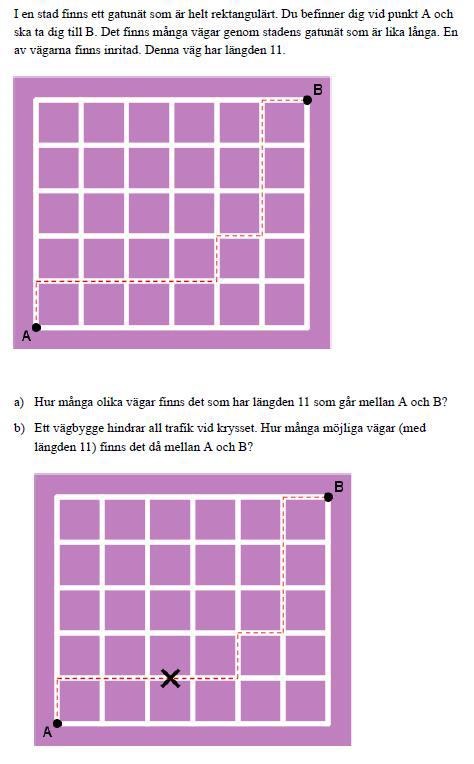
Hur många steg åt höger skall du gå totalt? Hur många steg uppåt skall du gå totalt? Du skall aldrig gå åt vänster eller neråt, för då blir längden mer än 11.
Kanske följande kan vara till nytta?
Vandringarna kan beskrivas som en följd av "högersteg" som vi kan beteckna med 0 och "uppsteg" som vi kan beteckna med 1.
Den inritade vandringen kan då beskrivas som 10000101110.
Kan du då översätta stadens geometri och villkoret på antal steg till krav på "ettor och nollor"-beskrivningen av vandringarna?
HEJ O TACK!
SÅ jag ska ha en ekvation och x o y ska vara lika beroende på hur många steg jag tar? kan ni förklara lite mer :)
Solver skrev:HEJ O TACK!
SÅ jag ska ha en ekvation och x o y ska vara lika beroende på hur många steg jag tar? kan ni förklara lite mer :)
Så här:
Du kan representera vandringen med hjälp av ett 11-siffrigt binärt tal bestående av 6 st nollor och 5 st ettor.
Det finns lika många sådana binära tal som det finns tillåtna vandringar i staden.
Frågan gäller då alltså hur många sådana binära tal det finns.
Då kan du börja med att se de 11 positionerna som tomma, välj ut 6 st av dessa positioner och stoppa in nollor där. Resten blir ettor.
Frågan är nu på hur många sätt du kan välja ut 6 positioner (element) ur en mängd med 11 positioner (element).
Ramlar polletten ner då?
Yngve skrev:Solver skrev:HEJ O TACK!
SÅ jag ska ha en ekvation och x o y ska vara lika beroende på hur många steg jag tar? kan ni förklara lite mer :)
Så här:
Du kan representera vandringen med hjälp av ett 11-siffrigt binärt tal bestående av 6 st nollor och 5 st ettor.
Det finns lika många sådana binära tal som det finns tillåtna vandringar i staden.
Frågan gäller då alltså hur många sådana binära tal det finns.
Då kan du börja med att se de 11 positionerna som tomma, välj ut 6 st av dessa positioner och stoppa in nollor där. Resten blir ettor.
Frågan är nu på hur många sätt du kan välja ut 6 positioner (element) ur en mängd med 11 positioner (element).
Ramlar polletten ner då?
omg jaaaaaaaaa det va smart!!
så det blir C(11,6) eller C(11,5) som är då 462 olika vägar
men hur göra man på b då? kan man använda samma metod?
Besläktad metod. Man behöver subtrahera alla vägar som går till punkten(2,1), sedan går åt höger och sedan går från (3,1) till mål. Dur många vägar är det?
Smaragdalena skrev:Besläktad metod. Man behöver subtrahera alla vägar som går till punkten(2,1), sedan går åt höger och sedan går från (3,1) till mål. Dur många vägar är det?
Hej!
blir det då C(7,4)=C(7,3) = 35 ?
i så fall svaret blir C(11,6)-C(7,4) =427
har jag gjort rätt?
Nej, 35 olika vägar som tas bort kan inte stämma - det finns tre olika sätt att komma från (0,0) till (3,1) så måste det vara något delbart med 3.
Smaragdalena skrev:Nej, 35 olika vägar som tas bort kan inte stämma - det finns tre olika sätt att komma från (0,0) till (3,1) så måste det vara något delbart med 3.
hur gör man då?
Solver skrev:Smaragdalena skrev:Nej, 35 olika vägar som tas bort kan inte stämma - det finns tre olika sätt att komma från (0,0) till (3,1) så måste det vara något delbart med 3.
hur gör man då?
Om du vill fortsätta med analogin binära tal så ska du från svaret i a-uppgiften ta bort alla de binära tal som
- har en nolla som fjärde siffra (dvs fjärde steget är ett "högersteg").
- har exakt en etta bland de första tre siffrorna (dvs endast ett av de tre första stegen är ett "uppsteg").
Klicka här för ledtråd
Dvs ta bort alla binära tal som inleds med någon av
1000XXXXXXX
0100XXXXXXX
0010XXXXXXX
Varje sådan möjlig inledning ska sedan följas av en avslutning XXXXXXX bestående av 3 nollor och 4 ettor.
Antalet sådana avslutningar är lika många som antalet 7-siffriga binära tal som består av exakt 3 nollor och 4 ettor. Frågeställningen känns bekant från a-uppgiften, eller hur?
Yngve skrev:Solver skrev:Smaragdalena skrev:Nej, 35 olika vägar som tas bort kan inte stämma - det finns tre olika sätt att komma från (0,0) till (3,1) så måste det vara något delbart med 3.
hur gör man då?
Om du vill fortsätta med analogin binära tal så ska du från svaret i a-uppgiften ta bort alla de binära tal som
- har en nolla som fjärde siffra (dvs fjärde steget är ett "högersteg").
- har exakt en etta bland de första tre siffrorna (dvs endast ett av de tre första stegen är ett "uppsteg").
Klicka här för ledtråd
Dvs ta bort alla binära tal som inleds med någon av
1000XXXXXXX
0100XXXXXXX
0010XXXXXXX
Varje sådan möjlig inledning ska sedan följas av en avslutning XXXXXXX bestående av 3 nollor och 4 ettor.
Antalet sådana avslutningar är lika många som antalet 7-siffriga binära tal som består av exakt 3 nollor och 4 ettor. Frågeställningen känns bekant från a-uppgiften, eller hur?
så det blir:
C(11,6)- 3* C(7,4) =357
en etta bland de första tre siffrorna : C(3,1)
varje möjlighet ska följas av en avslutning: C(7,4)
C(11,6)- C(3,1)* C(7,4) =357
har jag tänkt rätt?
Solver skrev:
så det blir:
C(11,6)- 3* C(7,4) =357
en etta bland de första tre siffrorna : C(3,1)
varje möjlighet ska följas av en avslutning: C(7,4)
C(11,6)- C(3,1)* C(7,4) =357
har jag tänkt rätt?

Yngve skrev:Solver skrev:så det blir:
C(11,6)- 3* C(7,4) =357
en etta bland de första tre siffrorna : C(3,1)
varje möjlighet ska följas av en avslutning: C(7,4)
C(11,6)- C(3,1)* C(7,4) =357
har jag tänkt rätt?
ahh tack för hjälpen!! :)




