Komplex analys - harmoniska funktioner

Resonemanget som du beskrivit det är inte helt korrekt. Nämligen är $f^\prime$ holomorf på $\mathbb{C} \setminus \{0\}$, men $f$ är inte det. Moreras sats / Cauchys integralsats innehåller ett extra villkor i implikationen åt ett av hållen. Satserna lyder:

Antag att $D \subset \mathbb{C}$ är en öppen mängd och $g: D \to \mathbb{C}$ är en kontinuerlig funktion.

• Om $\displaystyle\oint_\gamma g\left(z\right)\,dz = 0$ för varje sluten styckvis $\mathcal{C}^1$-kurva i $D$, så är $g$ holomorf på $D$.
• Om $g$ är holomorf på $D$ och $D$ är enkelt sammanhängande, så $\displaystyle\oint_\gamma g\left(z\right)\,dz = 0$ för varje sluten styckvis $\mathcal{C}^1$-kurva i $D$

Problemet är att $\mathbb{C} \setminus \{0\}$ inte är enkelt sammanhängande, så man kan inte dra slutsatsen att $g(z)=f^\prime(z)$ inte är holomorf.

Däremot är villkoret $\displaystyle\oint_\gamma g\left(z\right)\,dz = 0$ nödvändigt om det ska finnas en holomorf primitiv, så ditt resonemang funkar faktiskt fast man inte får påstå att $f^\prime(z)$ inte är holomorf.

Anm: Antag att $u(x,y) = \mathrm{Re} f(x+i\,y)$ för någon funktion $f \in \mathcal{H}(\mathbb{C}\setminus\{0\})$. Då är $f^\prime(z) = 1/z$.

Hur har ni/boken bevisat att funktionen $g(z) = 1/z$ saknar en holomorf primitiv på $\mathbb{C} \setminus \{0\}$?

Tillägg: 29 sep 2025 14:25

I mitt inlägg har jag tappat bort faktorn 2. Det borde ha nämligen varit $f^\prime(z) = 2/z$.

Bestäm du/dx samt du/dy och använd CR för att få två villkor på v. Försöker du lösa dessa genom att integrera ser du att det inte existerar någon funktion v som uppfyller CR och således är u ej realdelen av någon holomorf funktion.

Kruxet eller "problemet" är att den komplexa logaritmen är flervärd och behöver ett snitt (branch cut)

Ett enkelt sett att sätta fingret på vad saken gäller är att ställa upp CR i polära koordinater. Finns det $v(r,\theta)=v(r,\theta +2\pi)$?

Anto skrev:

Bestäm du/dx samt du/dy och använd CR för att få två villkor på v. Försöker du lösa dessa genom att integrera ser du att det inte existerar någon funktion v som uppfyller CR och således är u ej realdelen av någon holomorf funktion.

Det var detta jag anade var lösningen först. Vilket jag försökte göra, men det gick ej så bra. 

LuMa07 skrev:

Resonemanget som du beskrivit det är inte helt korrekt. Nämligen är $f^\prime$ holomorf på $\mathbb{C} \setminus \{0\}$, men $f$ är inte det. Moreras sats / Cauchys integralsats innehåller ett extra villkor i implikationen åt ett av hållen. Satserna lyder:

Antag att $D \subset \mathbb{C}$ är en öppen mängd och $g: D \to \mathbb{C}$ är en kontinuerlig funktion.

• Om $\displaystyle\oint_\gamma g\left(z\right)\,dz = 0$ för varje sluten styckvis $\mathcal{C}^1$-kurva i $D$, så är $g$ holomorf på $D$.
• Om $g$ är holomorf på $D$ och $D$ är enkelt sammanhängande, så $\displaystyle\oint_\gamma g\left(z\right)\,dz = 0$ för varje sluten styckvis $\mathcal{C}^1$-kurva i $D$

Problemet är att $\mathbb{C} \setminus \{0\}$ inte är enkelt sammanhängande, så man kan inte dra slutsatsen att $g(z)=f^\prime(z)$ inte är holomorf.

Däremot är villkoret $\displaystyle\oint_\gamma g\left(z\right)\,dz = 0$ nödvändigt om det ska finnas en holomorf primitiv, så ditt resonemang funkar faktiskt fast man inte får påstå att $f^\prime(z)$ inte är holomorf.

Anm: Antag att $u(x,y) = \mathrm{Re} f(x+i\,y)$ för någon funktion $f \in \mathcal{H}(\mathbb{C}\setminus\{0\})$. Då är $f^\prime(z) = 1/z$.

Hur har ni/boken bevisat att funktionen $g(z) = 1/z$ saknar en holomorf primitiv på $\mathbb{C} \setminus \{0\}$?

---

Tillägg: 29 sep 2025 14:25

I mitt inlägg har jag tappat bort faktorn 2. Det borde ha nämligen varit $f^\prime(z) = 2/z$.

Inses detta (att derivatan blir 2/z) av definitonen för den komplexa logaritmen eller för att

$\frac{2(x-iy)}{x^2+y^2}=\frac{2\bar{z}}{|z|^2} = \frac{2}{z}$?

Okej, nu löste jag det nog på det sättet jag tänkte först. Oklart varför det inte gick igår. 

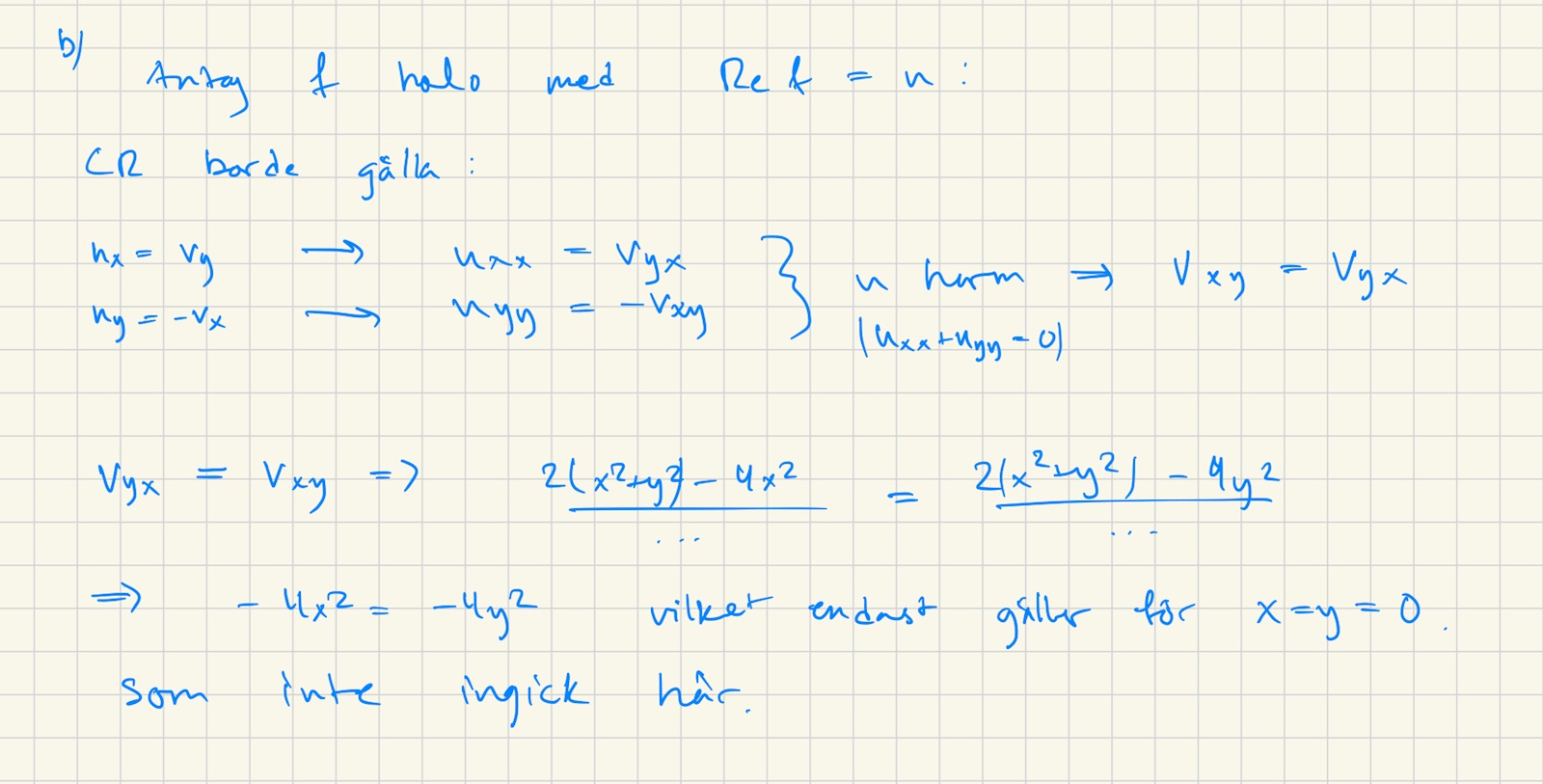
Ska kika på logartimgrejorna. 

MrPotatohead skrev:

Inses detta (att derivatan blir 2/z) av definitonen för den komplexa logaritmen eller för att

$\frac{2(x-iy)}{x^2+y^2}=\frac{2\bar{z}}{|z|^2} = \frac{2}{z}$?

Den komplexa logaritmen behövs inte för att inse att $f^\prime(z) = 2/z$, utan det följer från Cauchy-Riemanns ekvationer. CR ger att $f^\prime\left(z\right) = u^\prime_x\left(x,y\right) - i\,u^\prime_y\left(x,y\right) = \dfrac{2(x-iy)}{x^2+y^2}=\cdots = \dfrac{2}{z}$ (vilket du själv också skrivit)

När man insett att $f^\prime(z)=2/z$, så är det lätt att beräkna att $\oint_\gamma f^\prime\left(z\right)\,dz \ne 0$ då $\gamma$ är enhetscirkeln som genomlöps en gång moturs. Detta medför att det är omöjligt att värdet på $f(z)$ är lika med kurvintegralen längs en kurva inom $\mathbb{C} \setminus \{0\}$ från en given/fix punkt i $\mathbb{C}\setminus \{0\}$ mot punkten $z$, eftersom kurvintegralens värde skulle bero på vilken exakt kurva man valt i integralen. Detta strider mot analysens huvudsats då $f(z)$ skall vara lika med en sådan kurvintegral.

MrPotatohead skrev:

Det blev något teckenfel på denna rad. Både VL och HL borde ha $2(y^2-x^2)$ i täljaren, så de är lika överallt i $\mathbb{C}\setminus\{0\}$.

LuMa07 skrev:

Detta medför att det är omöjligt att värdet på $f(z)$ är lika med kurvintegralen längs en kurva inom $\mathbb{C} \setminus \{0\}$ från en given/fix punkt i $\mathbb{C}\setminus \{0\}$ mot punkten $z$, eftersom kurvintegralens värde skulle bero på vilken exakt kurva man valt i integralen. Detta strider mot analysens huvudsats då $f(z)$ skall vara lika med en sådan kurvintegral.

Okej, så analysens huvudsats säger att integralen bara beror på start- och slutvärde. Den gäller för holomorfa fkner (?) så när vi ser att integralen kommer vara annorlunda  beroende på kurva (för vi kan integrera över vilken som helst) så kan inte f vara holomorf. 

Är detta korrekt? Det känns som jag gör något väldigt fel här.

Tillägg: 16 okt 2025 22:12

Nää, nu blanda jag ihop det. Det är ju inte f som ska integreras.

Med analysens huvudsats syftade jag på följande identitet för (generaliserade) riemannintegraler:

$\displaystyle \int_a^b g\left(t\right)\,dt = G\left(b^-\right) - G\left(a^+\right)$

som gäller ifall funktionen $g: [a,b] \to \mathbb{C}$ är kontinuerlig på $[a,b]$ och $G(t)$ är en primitiv till $g$ på $(a,b)$, d.v.s. det gäller att $G^\prime(t) = g(t)$ för alla $t \in (a, b)$.

(Det finns en liknande sats för lebesgueintegraler där $g \in L^1(a,b)$ och $G$ är absolutkontinuerlig så att $G^\prime(t) = g(t)$ bara gäller nästan överallt i $(a,b)$.)

Anm: Notera att $g$ och $G$ tar in en reell variabel (och spottar ut komplexa tal). Derivatabegreppet $G^\prime(t)$ syftar alltså på den vanliga derivatadefinitionen från reell analys, d.v.s.

$\displaystyle G^\prime\left(t\right) = \lim_{h\to 0} \dfrac{G(t+h)-G(t)}{h}$,  där $h \in U \subset \mathbb{R} \setminus \{0\}$

Nu till uppgiften/beviset i frågan. Antag att $f(z)$ är holo på $\mathbb{C} \setminus \{0\}$. Låt $\gamma: [a,b] \to \mathbb{C} \setminus \{0\}$ vara en godtycklig slät kurva. Då är $G(t) = f(\gamma(t))$ en primitiv funktion till $g(t) = f^\prime(\gamma(t))\,\gamma^\prime(t)$ på $(a,b)$. Därmed gäller att

$\displaystyle \int_{\gamma} f^\prime\left(z\right)\,dz \stackrel{\text{def}}{=} \int_a^b f^\prime\left(\gamma\left(t\right)\right) \, \gamma^\prime\left(t\right)\,dt = f\left(\gamma\left(b\right)\right) - f\left(\gamma\left(a\right)\right)$.   $(\star)$

Kurvintegralens värde med integranden $f^\prime(z)$ beror alltså endast på värdena av den primitiva funktionen $f(z)$ i kurvans ändpunkter. (Kurvans exakta väg spelar alltså ingen roll.)

Hade det funnits $f(z)$ holo sådan att $\mathrm{Re}\,(f^\prime(z)) = \ln(|z|^2)$ gäller på $\mathbb{C} \setminus \{0\}$, så skulle denna $f$ strida mot $(\star)$. Med andra ord så skulle det leda till en motsägelse.

Jag tycker det vore synd att inte använda polära koordinater när man äntligen får chansen:

Om en reell funktion $u$ är harmonisk i ett enkelt sammanhängande område $D$ finns det en holomorf (analytisk) funktion $f(z)=u+iv$ vars reella del är $u$ (och vice versa för $v$). Funktionen $u=\ln(x^2+y^2)=2\ln(r)$ är harmonisk eftersom Laplace ekvation

$\displaystyle \Delta u=\frac{\partial^2 u}{\partial r^2}+\frac{1}{r^2}\frac{\partial^2 u}{\partial \theta^2}+\frac{1}{r}\frac{\partial u}{\partial r}=0$

är uppfylld för $r>0$ (dvs i området frågan gäller). Vi kan därmed på en reell konstant när bestämma ett harmoniskt konjugat $v$ så att CR-ekvationerna uppfylls och $f(z)=u+iv$ är holomorf i ett enkelt sammanhängande delområde av $\mathbb{C}\setminus\lbrace 0\rbrace$ . I polära koordinater blir det

$\displaystyle \frac{\partial u}{\partial r}=\frac{1}{r}\frac{\partial v}{\partial \theta},\quad \frac{\partial v}{\partial r}=-\frac{1}{r}\frac{\partial u}{\partial \theta}$

och det visar sig direkt att $v=2\theta +C$ där $C$ är en reell konstant. Med andra ord är $f(r,\theta)=2(\ln(r)+i(\theta+C))$. Men detta är ju definitionen av $f(z)=2\log(z)$!

Uppenbarligen är $2\log(z)$ inte kontinuerlig i $z=0$, eftersom den inte ens är definierad där. Väljer vi principalgrenen är funktionen inte heller kontinuerlig över den utskurna negativa delen av $x$-axeln $(x<0, y=0)$. På den övre sidan har argumentet värdet $v=2\pi$, medan det på den undre sidan är $v=-2\pi$. Funktionen $v$ gör alltså ett diskontinuerligt hopp om $4\pi$ när vi korsar det utskurna grensnittet (branch cut).

Eftersom $v=2\theta +C$ ändrar värde med $4\pi$ vid ett varv runt origo finns det inget sätt att göra $2\log(z)$ analytiskt på hela $\mathbb{C}\setminus\{0\}$. Däremot är $u$ den reella delen av en holomorf funktion $f=2\log(z)$ i varje enkelt sammanhängande delområde av $\mathbb{C}\setminus\{0\}$ som inte innehåller det valda grensnittet (branch cut) .