Komplex ström
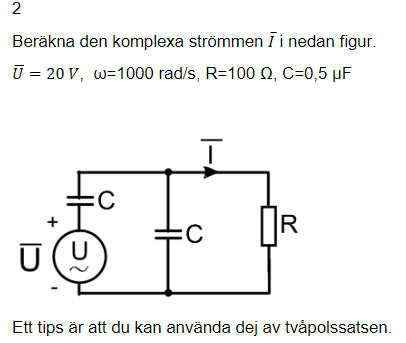
U=20V w=1000rad/s R=100 Ohm C=0,5uF F=159hZ
vinkel U=20/√ 3*20=0,577= tan-1 0,577=30 grader
Xc= 1/2*pi*159*1*10^-10 = 1000,97
Z=√ R^2*Xc^2 = 1005,95
cosfi R/Z =0,099= 84,29 grader
I= U/Z= 20/1005,95=0,0198=0,02A
vinkeln 30-84,29=-54,29grader
I=0,02 <-54,29
kan det stämma eller är jag helt ute och cyklar? Är sjukt osäker på det här. känns som jag snubblar fel lite här och var.
Eller.. Är det så enkelt att det är I=U/R = 20/100=0,2A vinkel 0 grader ?
Nej det fungerar nog inte med bara Ohms lag här.
Några frågor:
Vad är det för vinkel du räknar ut till 30 grader?
Vad är Xc? Impedansen för en av kondensatorerna är
Vad är Z?
Ledsen för alla motfrågor men jag blev lite förvirrad :-)
Vinkeln 30 grader är.. Ja, bra fråga. En vinkel på spänningen jag snubblade över i ett exempel som jag fick för mig jag behövde h med här för att få fram rätt vinkel till I.
Xc räknade jag 1/2*pi*F*C . Räknade ut F istället för w.
C=1 för jag räknade ihop dom båda kondensatorerna på 0.5uF till en, slog ut den som ett Xc och räknade den mot R för att få fram mitt Z. För att sedan t U/Z.
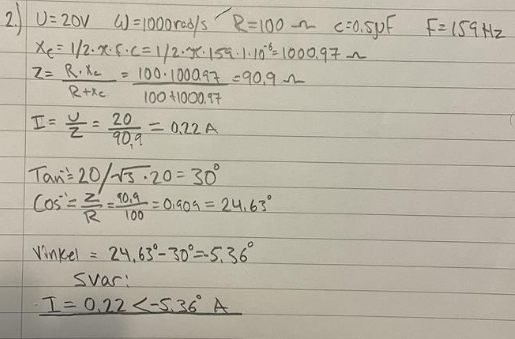
så räknade jag ut den nu. Men än en gång, jag kanske är helt fel ute.
En korrigering -
Jag tolkar det så att spänningen på polär form är V
Om man vill överslagsräkna kan man se att impedansen hos kondensatorerna är mycket större än resistorns impedans (resistans) och då ganska snabbt komma fram till strömmen I
Annars blir det omfattande beräkningar av totalimpedans, totalström och delström I via strömgrening med komplexa tal på båda formerna (polär resp rektangulär form)
Det finns ju ett viktigt tips i uppgiften: Du kan använda tvåpolssatsen.
Den innebär att en krets med en spänningskälla och diverse impedanser kan ersättas med annan spänningskälla och en serieimpedans.
https://en.wikipedia.org/wiki/Th%C3%A9venin%27s_theorem
Gör en tvåpol av spänningskällan och de två kapacitanserna:
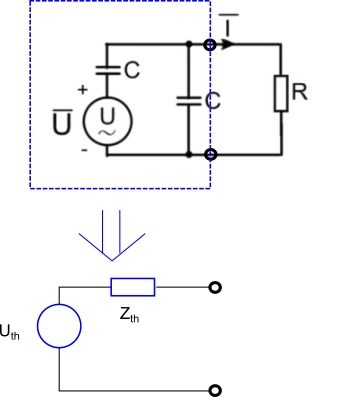
Det blir enklare (men inte lätt) och du måste använda komplexa tal, "jw-metoden"
Gör jag det genom att räkna om C=0,5μF, till Xc=2000Ω med uträkning: XC=1ωC=11000⋅0,5⋅10−6=2000 ΩXC=1ωC=11000·0,5·10-6=2000 Ω ?
Så att det blir som 3 resistanser varav kondensatorerna blir på 2000Ω styck?
Z= R/Xc= 100Ω*4000Ω/100Ω+4000Ω=97,5Ω
I=U/Z=20V/97,5Ω=0,21A
Om jag ska räkna tvåpolssats får jag det till:
V
Här känner jag att jag blandar ihop delar av flera sätt till något obegripligt.
Kondensatorns impedans blir: -j2000 ohm. Glöm inte att det handlar om komplexa impedans, därav -j. Om du räknar med kondensatorns impedans som en ren resistans så blir det fel.
Att räkna ut Uth och Zth med tvåpolssatsen görs i två steg:
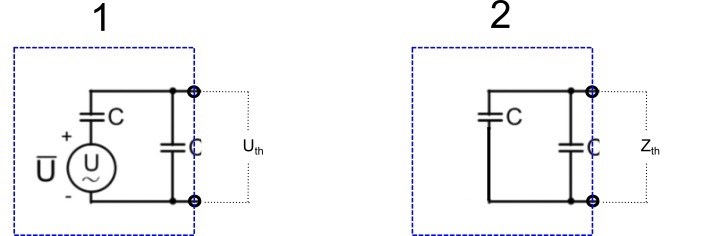
1. Ta bort R och räkna ut vad spänningen Uth blir.
2. Kortslut spänningskällan och och räkna ut impedansen blir över tvåpolens anslutningar. Zth blir också en komplex impedans.
=-j1000Ω
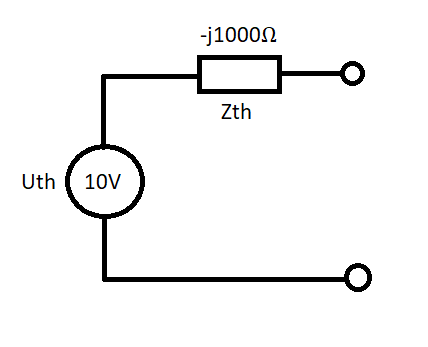
Är jag rätt ute?
Yes!
"Koppla in" motståndet och räkna ut den komplexa strömmen.
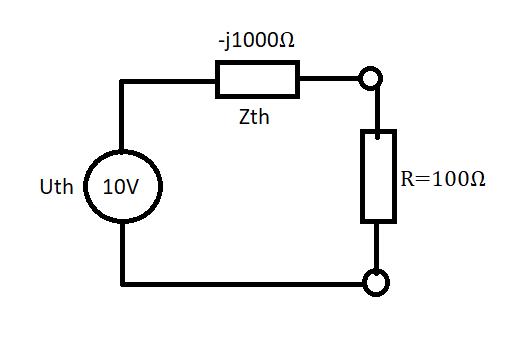
tan phi =-j1000/100= -84,28°
Kan detta ha blivit rätt?
Hur fick du fram I = -j0.01A ?
Om strömmen är -j0.01 så är fasvinkeln exakt -90 grader. Strömmen är inte rent imaginär, den har en lite real komponent också.
Det phi du räknat ut är för den totala impedansen. När du sedan ska räkna ut strömmen som I = Uth/Ztot så blir vinkeln +84.28.
tan phi =-j1000/100= -84,28°
Det sista likhetstecknet ska ju inte stå där. Det borde vara tan phi =-j1000/100 phi = -84,28°
Jag förstår att det är så du menar och jag är kanske petig men om du skriver så på en tenta så riskerar du poängavdrag.
I=−j0,01A <−84,28°
Använd polärt format eller formatet a+jb. Inte båda på en gång. Åter igen, jag kanske är lite petig men det ser konstigt ut.
Jag uppskattar petigheten, den är bara till hjälp!
Jag tänkte I=U/Z+R = 10V/-j1000Ω+100Ω=-j0,01A
Hur blir det +84,28° och inte minus som uträkningen ger? Den är väl uppenbarligen inte korrekt, men förstår inte hur?
Hur menar du med formatet? Kan jag inte skriva svaret som jag gjort? I=−j0,01A <−84,28°?
Jag tänkte I=U/Z+R = 10V/-j1000Ω+100Ω=-j0,01A
Nej, den där divisionen stämmer inte. Det är som om du hade gjort:
Det är ju ett komplext tal i nämnaren som vi måste göra något åt. Då kan man använda något som kallas "komplexa konjugatet". Har du ett komplext tal, t.ex. 3-j10, så är dess komplexa konjugat: 3+j10.
En annan användbar sak är att j2 = -1
Om vi använder detta i vår uppgift så får vi:
Vips har vi ett tal utan komplex nämnare. Och detta är strömmen som vi kämpat så för att få fram!
I ett komplext tal-plan ser det ut något så här:
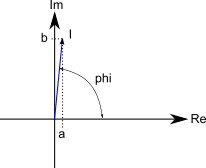
Du kan ange strömmen I på formatet a+jb eller som absolutbeloppet (längden på pilen) och vinkeln phi.
I vårt fall blir a=0.99*10-3 och b=9.9*10-3
Det här var bra mycket mer än vad jag var inne på från början kan man säga. Och fortfarande ser jag inte hur jag får fram svaret.. Vad mitt I är och vilken vinkel. Eller vinkeln bör bli 84.28, tror jag. Men mitt I förstår jag inte. Och vad hände när j=-10m? Hur kan det vara det och vad hjälper den?
Är mitt I = 0.99*10^−3 +j9.9*10^−3. förstår tyvärr inte.
Många frågor, jag är otroligt tacksam att du orkar med alla dumma frågor.
Som någon vis person sagt, det finns inga dumma frågor. Bara dumma svar.
Här blev det nog fel:
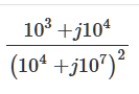
1002 = 10000 = 104 och
10002 = 1000000 = 106 och
j2 = -1
Uppgiften frågar efter den komplexa strömmen I genom resistorn och den är 0.99*10-3 + j9.9*10-3 . Uppgiften säger inte i vilket format vi ska ange den så detta borde duga.
Ett alternativt sätt är att använda polärt format med absolut beloppet och vinkeln från reella axeln. Det blir i så fall:
Båda sätten beskriver matematiskt figuren i mitt förra inlägg.
blir det inte så? Kanske hänger upp mig på fel saker nu.
Sen hur slår du det för att få det till ,99 och 9,9 ? Alltså vilka värden? Att det höjs upp i 10^-3 förstår jag eftersom det blir mA.
hur du slår 1+j10/1010 ? Eller har det slagits fel där någonstans?
Jag vill hänga med i alla steg, därav alla osammanhängande frågor.
Jag vill hänga med i alla steg, därav alla osammanhängande frågor.
Bra! Man ska inte ge upp så lätt.
Den första termen har ett fel i nämnaren. Där ska stå:
Det ser ut som (j1000)2 strular till det för dig. Det blir så här: (j1000)2 = j2 * 10002
10002 blir ju 106 och j2 blir -1. Så (j1000)2 = -1 * 106 = -106 . I uträkningen fanns det redan ett minustecken så det blir plus
Jag hoppas ni har gått igenom hur man räknar med komplexa tal annars blir denna uppgiften väldigt svår.
Aha, ja såklart. j^2 =-1. Den lilla detaljen bommade jag helt. Det ger potensräkning är väl högstadiematte men det satt långt inne innan det kopplade. Nu är jag med på alla stegen.
Jodå, vi har gått igenom det men uppenbarligen fastnade inte så mycket. Helt klart att det kapitlet behöver mer uppmärksamhet.
Stort stort tack för ditt tålamod och dina svar, det uppskattas verkligen!
Insåg att allt inte var glasklart ändå.. Tidigare i ekvationen, när jag får fram kondensatorns impedans till -j2000Ω, blir den -j bara för att det är komplexa impedansen eller måste jag ta med j tidigare?
XC=1ωC=1/1000⋅0,5⋅10−6=2000 Ω = -j2000Ω ? Eller ändra den ekvationen till
XC=1ωC=1/1000⋅j0,5⋅10−6 ? Så att kondensatorerna skrivs som j0,5 direkt, eller -j0,5 kanske det ska vara?
Kondensatorns impedans XC = 1/(jωC) = -j/(103•0,5•10-6) = -j2000 Ω.
1/jωC Ja men just de. Den kände jag igen, den har jag sett förut. Tack för svar!
Det kan löna sig att vara envis.
Och, om man inte frågar får man heller inga svar.
Absolut! Tack än en gång!



