Komplexa tal
Hej
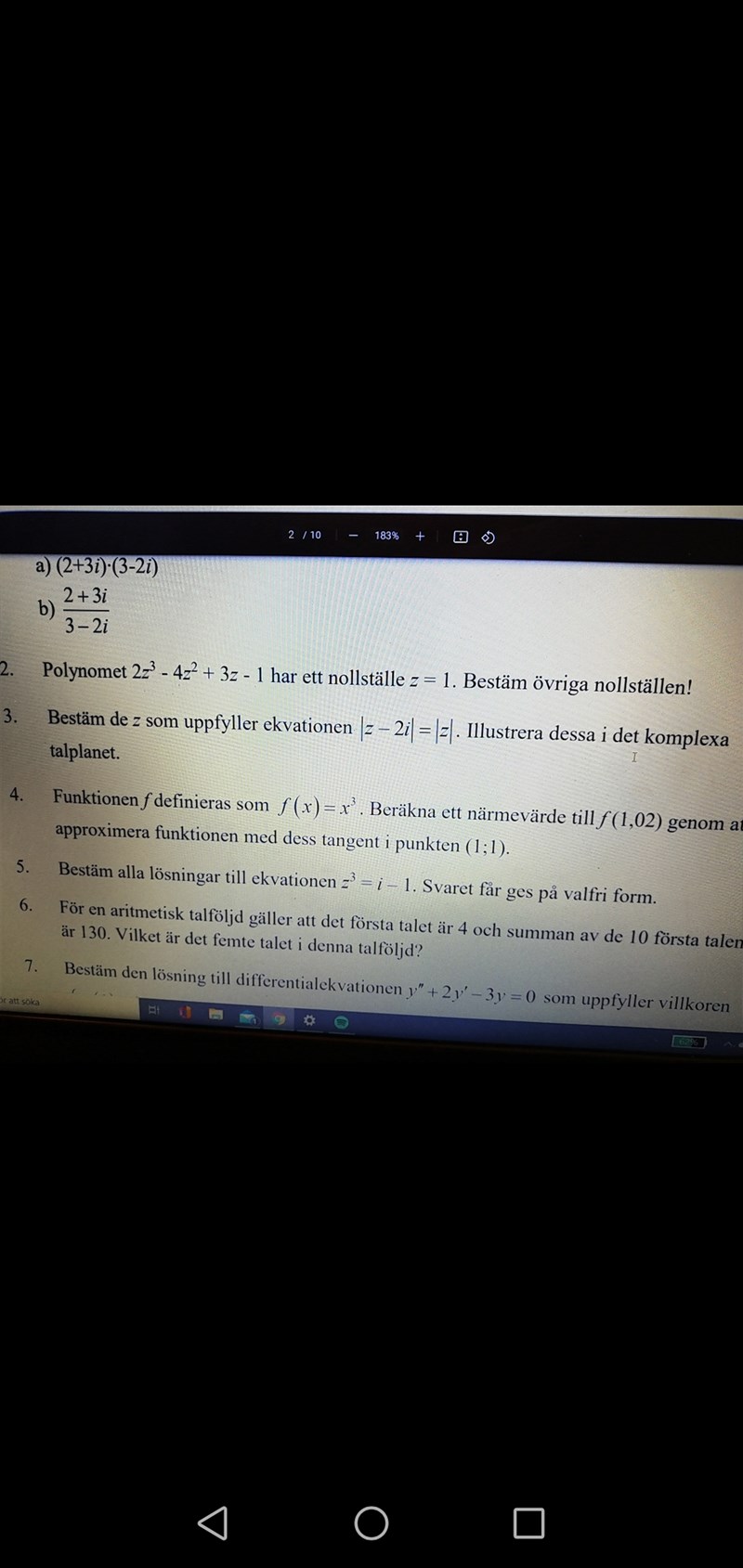
Uppgift 3. Undrar hur man går från det nästsista steget till det sista steget?
De multiplicerar ju inte ihop alla termer som vanligt, varför? Och varför tar de bort i?

Mvh
Det näst sista steget ser fel ut men sen fortsätter det som om de hade skrivit rätt.
Näst sista raden borde vara | a+bi-2i |2 = | a+bi |2
Sen använder man att detta kan du testa med |a+bi| och se om det stämmer
Där är det komplexa konjugatet till z
Eftersom det är skrivet för hand så gissar jag att personen i fråga råkat skriva fel. Om man på näst sista raden ersätter alla b med b*i så ser uträkningen mer rimlig ut.
Angående lösandet av ekvationen: man kan se det som att man tar att |z-2i| = |z-0|, vilket avslöjar att alla lösningar måste ha samma avstånd till origo (koord: (0,0)) och 2*i (koord: (0,2)).
Om man ritar detta i talplanet och tänker lite kanske man kan hitta lösningarna utan att använda formler, även om detta givetvis är görbart och antagligen det mest givande sättet att göra det på.
Bedinsis skrev:Eftersom det är skrivet för hand så gissar jag att personen i fråga råkat skriva fel. Om man på näst sista raden ersätter alla b med b*i så ser uträkningen mer rimlig ut.
Angående lösandet av ekvationen: man kan se det som att man tar att |z-2i| = |z-0|, vilket avslöjar att alla lösningar måste ha samma avstånd till origo (koord: (0,0)) och 2*i (koord: (0,2)).
Om man ritar detta i talplanet och tänker lite kanske man kan hitta lösningarna utan att använda formler, även om detta givetvis är görbart och antagligen det mest givande sättet att göra det på.
Har inte råkat skriva fel, det är jag som inte förstår konceptet
Försökte tolka detta

Förstår hit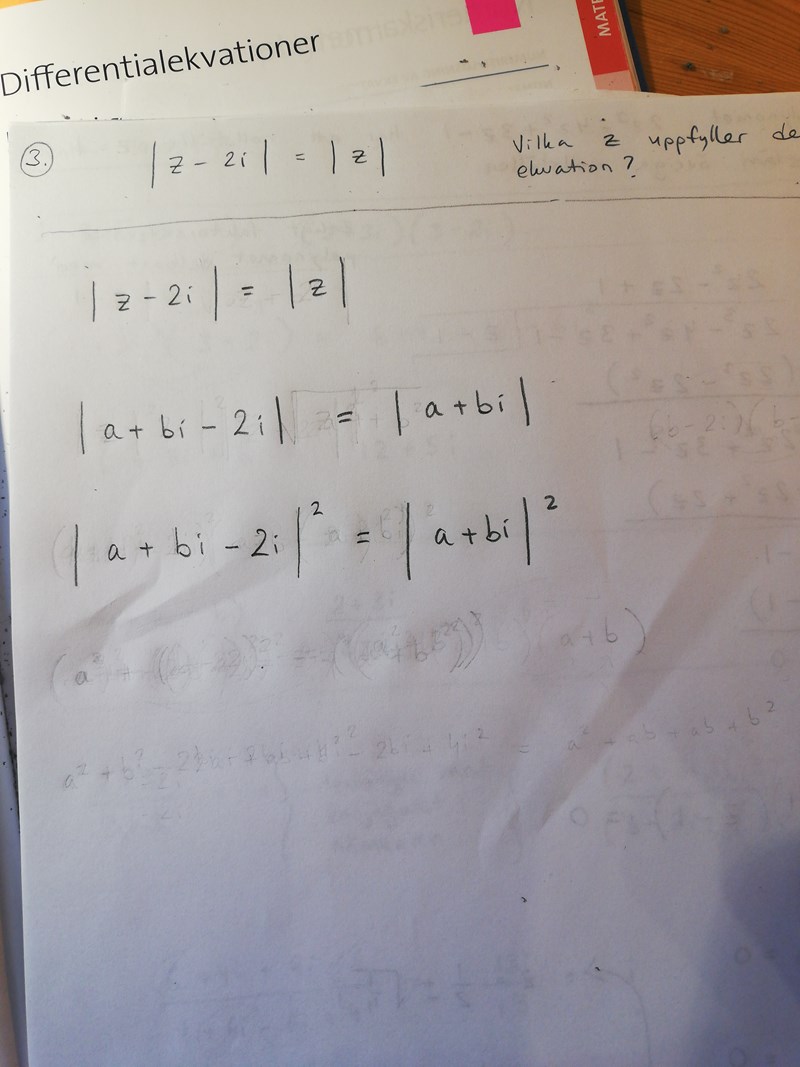
Absolutbeloppet av ett komplext tal ges av kvadratroten ur kvadraten av realdelen + kvadraten av imaginärdelen, dvs
om
Om vi tittar på den nedersta raden du skrivit så har du
Högerledet kan räknas ut med sambandet jag hämtade från länken:
Vänsterledet kan skrivas om en smula till:
eftersom att imaginärdelen tydligen är b-2.
Detta ger
Låter man upphöjt till två och roten ur ta ut varandra så får man
vilket var där du fastnade, om jag tolkat dina två sista inlägg rätt.
Tack för hjälpen
Undrar om det även går att lösa den här uppgiften såhär?
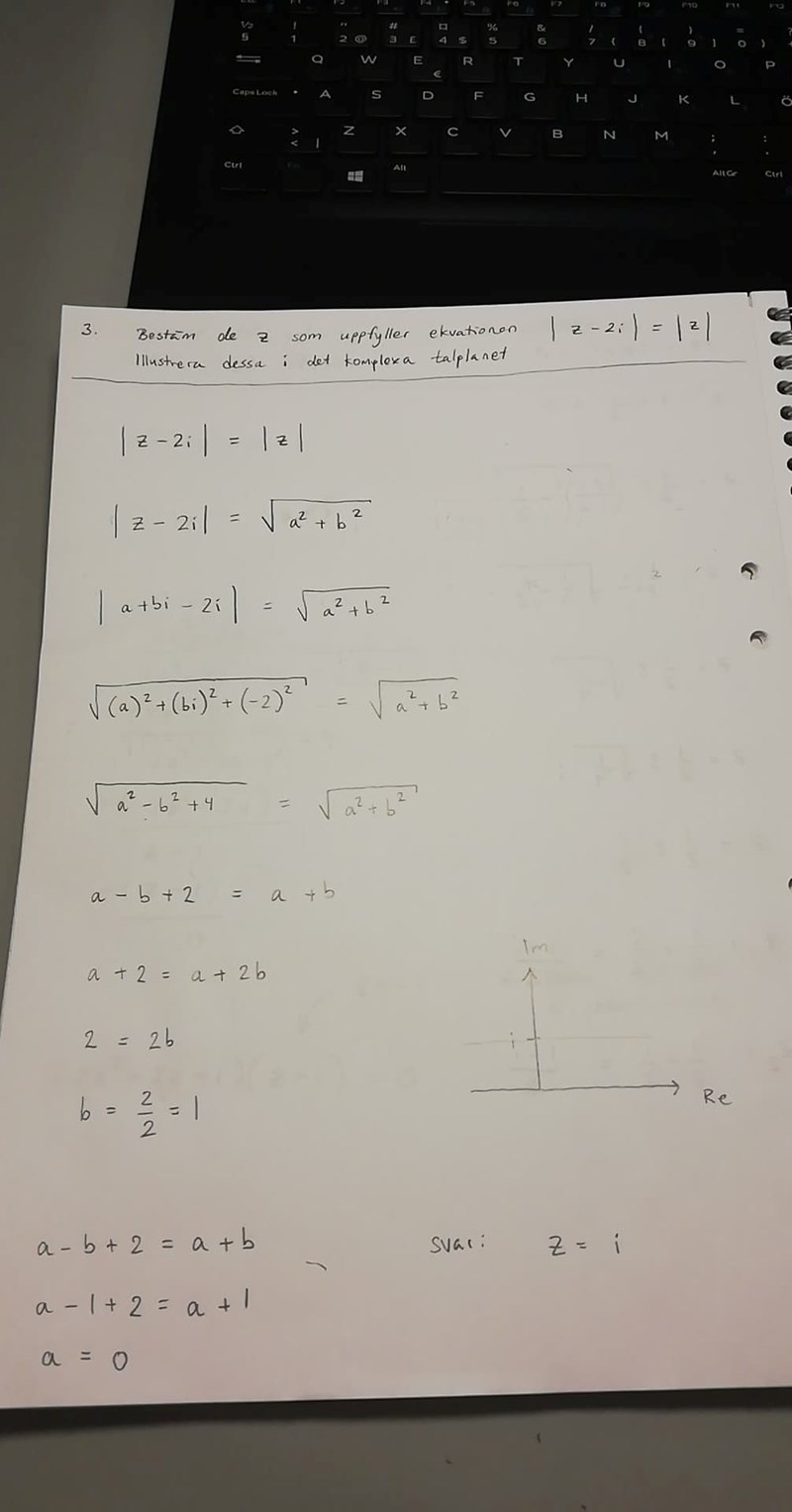
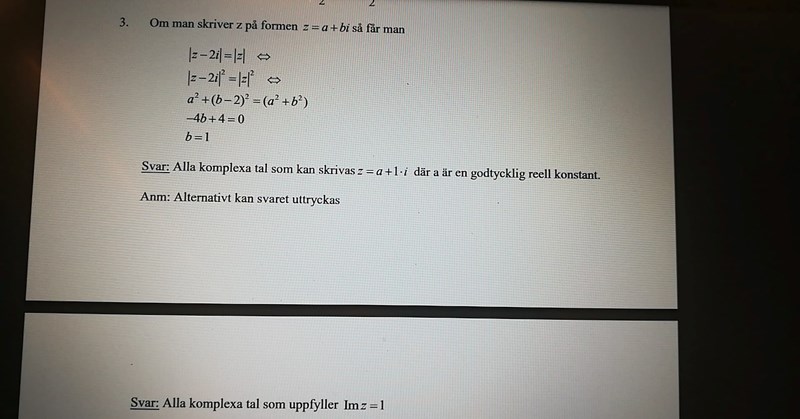
Om du menar att , så är det inte så.
Okej, tack. Håller mig till facit
ct1234 skrev:Okej, tack. Håller mig till facit
Hej, har en snabb fråga jag är en i matte 4!
Varför bytte du Z mot a^2 +b^2 i höger ledet medan i vänstra ledet bytte du Z mot a+bi.
Snälla kan du svara mig
Vilken rad menar du?
Skriv av raden (och raden innan).
joculator skrev:Vilken rad menar du?
Skriv av raden (och raden innan).
Det var dessa rader:
l Z-2il= l Z l
l Z-2il=roten ur (a^2+b^2)
la+bi-2il= roten ur (a^2+b^2)
Varför i rad 2 blev Z som roten ur (a^2+b^2)) och i rad 3 så bytts det Z mot a+bi?
Alla komplexa tal kan skrivas på formen a+bi. Man har alltså bytt ut z mot a+bi för att kunna räkna vidare.
Smaragdalena skrev:Alla komplexa tal kan skrivas på formen a+bi. Man har alltså bytt ut z mot a+bi för att kunna räkna vidare.
Tackar
Men sist varför lZl bytts mot roten ur (a^2+b^2) om du kollar på högra leden i steg i och 2
Tack igen
Det är så man beräknar |z|, d v s absolutbeloppet av z. Det ä r egentligen bara Pythagoras sats!





