komplexa tal
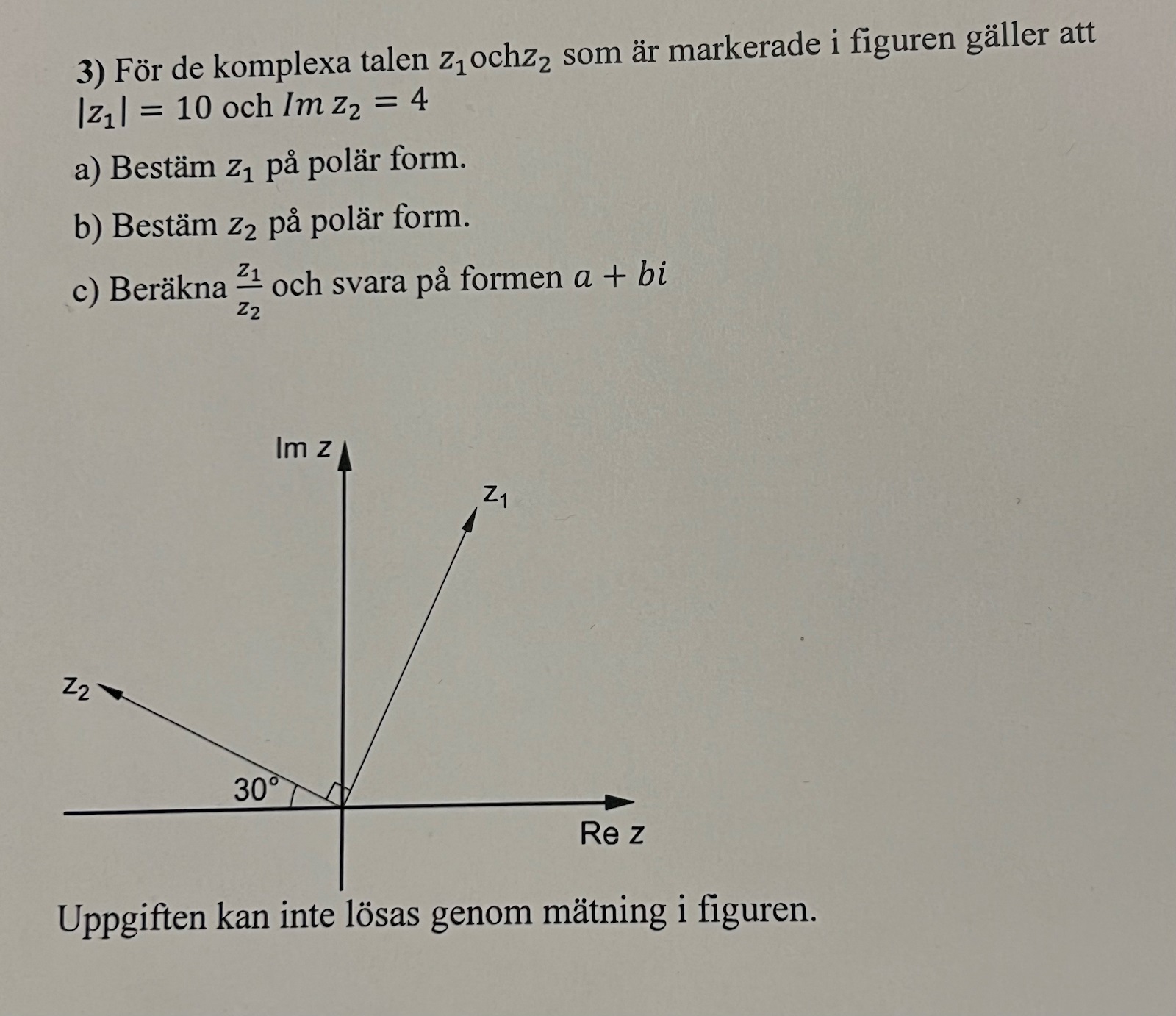
Jag behöver hjälp med första och andra delfrågan. Någon som kan visa mig dom första beräkningarna man ska göra?
Så tacksam för hjälp.
Vet du vad polär form innebär? Vad får du för information i uppgiften?
Ja jag vet vad polär form är. Vill du visa mig hur jag ska börja?
Vad är vinkeln mellan Z1 och Re-axeln?
60
Om du visste vad polär form är så borde du väl kunna lösa den då?
Om jag kunde lösa den skulle jag ju uppenbarligen inte ställa frågan här. Jag vet vad polär form är. Vill du hjälpa mig eller bara ställa motfrågor haha?
Försöker hjälpa dig här. Du har nog inte så bra koll som du tror men förklarar gärna:)
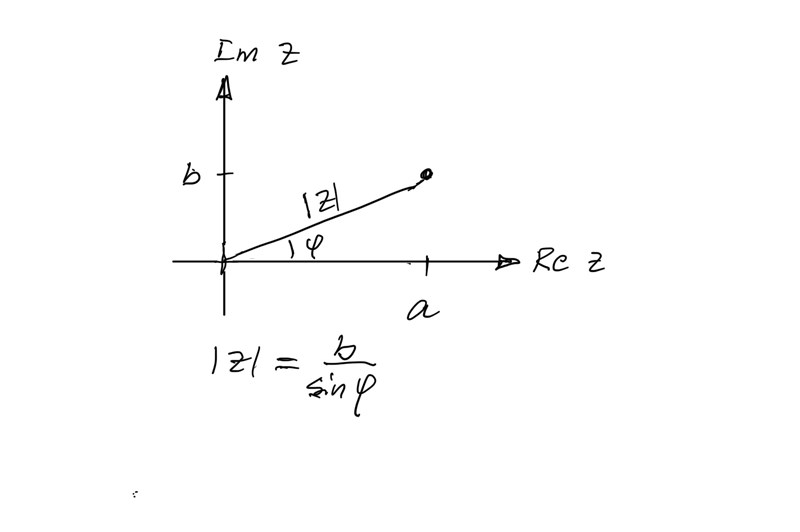
Komplexa tal kan skrivas a+bi. Detta är med en realdel a, en imaginärdel b och imaginär enhet i. I det komplexa talplanet ovan kan komplexa tal beskrivas som punkter (a,b). Dessa tal även skrivas i polär form, en form som innefattar trigonometriska funktioner enligt:
där är absolutbeloppet för Z. Med andra ord avståndet mellan origo och punkten det komplexa talet utgör.
v är argumentet för Z och är vinkeln mellan pilen, som går mellan origo och punkten, och Re-axeln.
I ditt fall får vi direkt absolutbeloppet och du beräkna argumentet till 60 grader.
Hur blir det då i polär form om du utgår från formen jag skrev ovan?
Läs här om det fortfarande är oklart med polär form: https://www.matteboken.se/lektioner/matte-4/komplexa-tal/komplexa-tal-i-polar-form#!/
Hur vet du att absolutbeloppen z1=10? Så svaret på första är 10(cos(60)+isin(60)) har jag kommit fram till rätt?
Wbd554 skrev:Hur vet du att absolutbeloppen z1=10? Så svaret på första är 10(cos(60)+isin(60)) har jag kommit fram till rätt?
Du får det ju i frågan, precis som jag tipsa dig om att kolla efter i inlägg #2.
Ja, det stämmer.
Ok haha trött. Då tänker jag att svaret på 2an är 4(cos(150)+isin(150)) ?
I så fall blir ditt svar -2√3 + i2, och det kan ju inte vara rätt. Det går ju också att kolla sina beräkningar själv.
Vad menar du Jan? Det är väl absoultbeloppet av 4 som är 4? Eller bör jag göra på något annat sätt?
Im z2 = 4 innebär att den imaginära delen i z2, dvs b om det skrivs i a+bi, är 4
Okej men vad ska jag göra nu då? Hur beräknar jag absolutbeloppet i b) uppgiften? För det är väl nästa steg?
tan 150 = 4/a? Förstår inte...
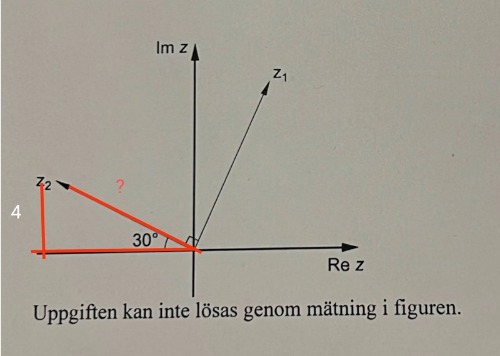
Underlättar den här bilden? Kan du lösa ut "?" (m.a.o z2)
Hojta till om något är oklart.
det blir 8 :)
Ahaaa, så svaret blir därmed 8(cos150+isin150), right?
Det stämmer! Men förstår du varför? Om inte, skriv så kan jag förklara.
alltså du får gärna förklara :)
Att skriva om till polär form innebär att man skriver i formen
Z = I z I (cos(v) + i sin(v)
Där I Z I är längden på vektorn och vinkeln (v) är vinkeln avläst moturs med start från första kvadranten.
A)
I uppgiften får vi veta att längden på vektorn z1 är 10, genom beteckningen ( I Z1 I = 10 ). Sedan kan vi utifrån figuren avläsa vilken vinkel.
Vilket fås till
Är du med på detta?
Tillägg: 5 jan 2024 23:42
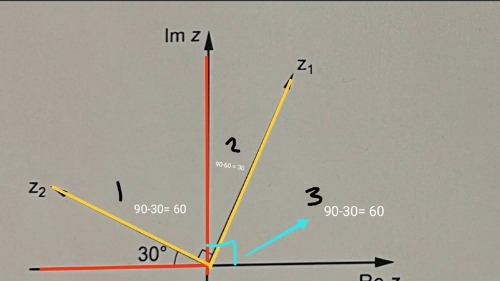
Varje kvadrant är 90 grader.
Sedan (gul figur) är ocks 90 grader, och dessutom får vi en given vinkel (30 grader). Genom att få reda på vinkeln i område 1 (sträcka mellan röd och gul) tar vi alltså 90-30 = 60 grader.
Därefter kollar vi på första kvadranten och räknar ut att område 2 (mellan gul och röd) måste vara 90-60 = 30.
Till sist får vi att 90-30 = 60 grader.
Därmed är vinkeln för z1 = 60 grader.
För b)
Vi har endast givet att den imaginära delen för z2 är 4 genom ( Im z2 = 4 ).
Den imaginära delen finner du alltid i y-axeln, därmed är koordinaten för z2 ( x, 4).
(vi vet inte vad x är, därför namnger vi den som okänd).
Eftersom vi vet vinkeln, och en katet, kan vi med hjälp av trigonometri räkna ut z2 (hypotenusan) i vår triangel.
Detta gör vi genom sinus, som du fick till 8.
Alltså vet vi nu att vektorn, I z I = 8.
Vinkeln räknade du också ut korrekt, 180-30 = 150.
Hojta till om du har frågor eller inte förstår.
Tack så för din förklaring, du är så bra på att förklara! Tack! :-)