Komplexa tal fråga
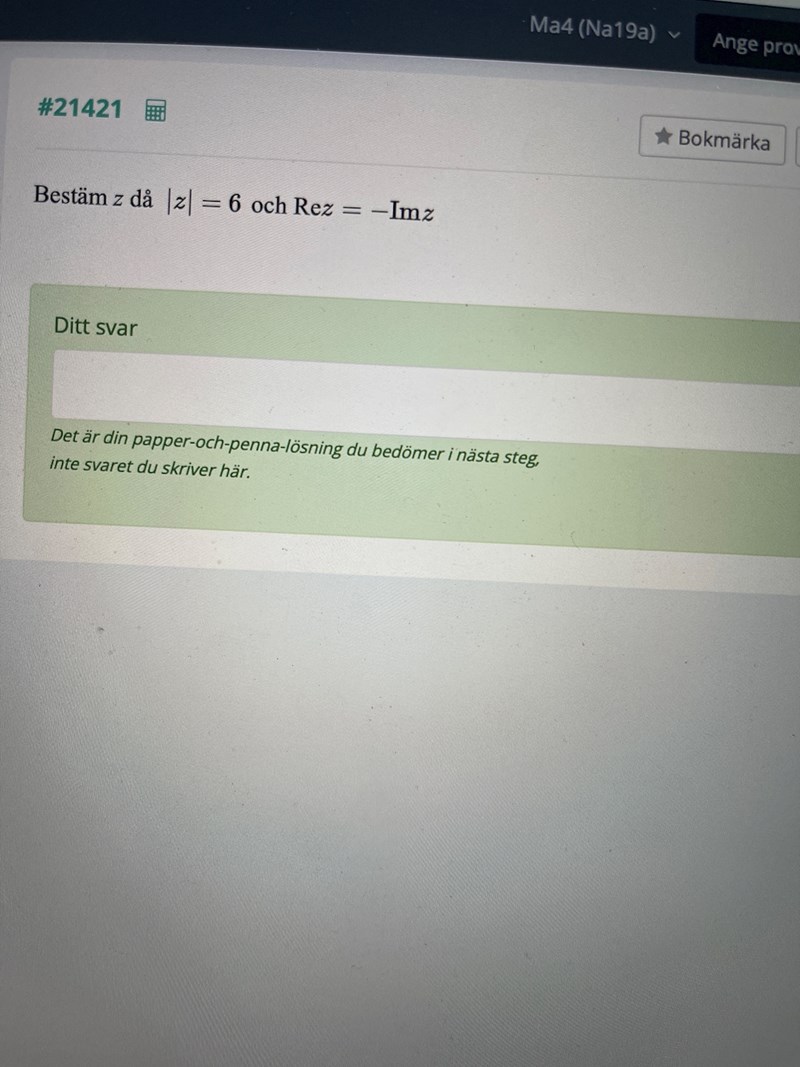
Hej! Jag behöver ha hjälp med den här frågan. Att absolutbeloppet av z är 6 betyder att radien är 6
Katarina149 skrev:
Hej! Jag behöver ha hjälp med den här frågan. Att absolutbeloppet av z är 6 betyder att radien är 6
Det är en bra början.
Sätt sedan z=a+bi
Vilket krav får du på a och b då Re(z)=-Im(z)?
då är b= -a
då blir z= a-ai
absolutbeloppet av z är a+ai vilket är lika med 6
Hur gör jag sen?
Absolutbeloppet av ett komplext tal ges av , inte det du skrivit.
Vad är då absolutbeloppet för ditt ?
EDIT - samma som Moffen skrev
Moffen skrev:Absolutbeloppet av ett komplext tal ges av , inte det du skrivit.
Vad är då absolutbeloppet för ditt ?
Absolutbeloppet ska då vara
Detta ger till sist att z=a-ai
a har jag redan beräknat. Alltså blir det ->
Men i facit står det så här . Så jag verkar ha räknat fel
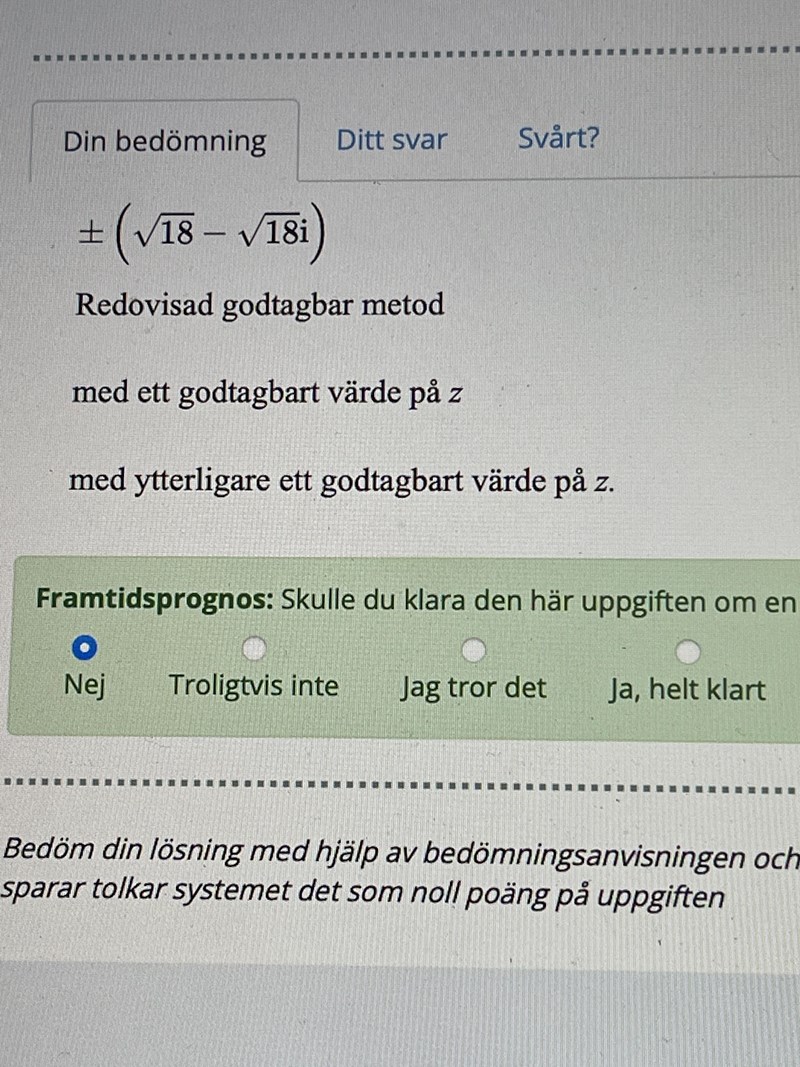
Om du förlänger ditt komplexa tal med och förenklar så får du samma svar som i facit, förutom att du missade .
ja juste jag tar ju roten ur därför måste det vara +-
Katarina149 skrev:ja juste jag tar ju roten ur därför måste det vara +-
Nej det är inte därför.
Det är för att Re z = -Im z inte automatiskt innebär att Re z > 0 och Im z < 0, det kan lika gärna vara tvärtom.
Inte heller villkoret |z| = 6 ger oss någon information om vilket tecken Re z och Im z har.
Yngve skrev:Katarina149 skrev:ja juste jag tar ju roten ur därför måste det vara +-
Nej det är inte därför.
Det är för att Re z = -Im z inte automatiskt innebär att Re z > 0 och Im z < 0, det kan lika gärna vara tvärtom.
Inte heller villkoret |z| = 6 ger oss någon information om vilket tecken Re z och Im z har.
Jag vet inte riktigt om jag förstår vad du menar
Yngve skrev:Katarina149 skrev:ja juste jag tar ju roten ur därför måste det vara +-
Nej det är inte därför.
Det är för att Re z = -Im z inte automatiskt innebär att Re z > 0 och Im z < 0, det kan lika gärna vara tvärtom.
Inte heller villkoret |z| = 6 ger oss någon information om vilket tecken Re z och Im z har.
Det håller jag nog inte med om. Uträkningarna visar, genom att använda att , att . Visst kan man argumentera som du gjort också, men gör man uträkningarna rätt så får man även fram .
Moffen skrev:Yngve skrev:Katarina149 skrev:ja juste jag tar ju roten ur därför måste det vara +-
Nej det är inte därför.
Det är för att Re z = -Im z inte automatiskt innebär att Re z > 0 och Im z < 0, det kan lika gärna vara tvärtom.
Inte heller villkoret |z| = 6 ger oss någon information om vilket tecken Re z och Im z har.
Det håller jag nog inte med om. Uträkningarna visar, genom att använda att , att . Visst kan man argumentera som du gjort också, men gör man uträkningarna rätt så får man även fram .
Tänkte jag alltså rätt?
Ja, det tycker jag (om du kommer ihåg !). Du har ansatt ett godtyckligt reellt tal som den reella delen utan några extra antaganden och fortsatt lösa uppgiften utifrån det.
Katarina149 skrev:
Tänkte jag alltså rätt?
Det beror på vilken rotutdragning du menade.
Jag trodde att du menade att |z| = 6 innebär att |z| = 6, vilket inte stämmer.
Katarina149 skrev:Moffen skrev:Absolutbeloppet av ett komplext tal ges av , inte det du skrivit.
Vad är då absolutbeloppet för ditt ?
Absolutbeloppet ska då vara
Det är så jag tänkte
Katarina149 skrev:
Det är så jag tänkte
OK då saknas det bara ett där, precis som Moffen skrev.


