Komplexa tal hur fortsätter jag?
Hej, hur löser man b?

Jag har kommit så här långt:

Men jag har fastnat så antingen har jag gjort fel eller så vet jag bara inte hur jag ska ta mig vidare.
Tänk så här istället
a) Du kan skriva ekv. som
|z–(–1)| = |z–2|
Vilka punkter har lika långt till -1 som till 2? Det självklara svaret är den punkt som ligger mitt emellan, z=1/2, men det finns fler!
b) löser du på samma sätt.
 Jag löste a så här. Jag vet inte om du förstår för jag skrev det ganska slarvigt. Sedan försökte jag göra på samma sätt för b men det gick inte.
Jag löste a så här. Jag vet inte om du förstår för jag skrev det ganska slarvigt. Sedan försökte jag göra på samma sätt för b men det gick inte.
Jag hittade en tråd här med en liknande uppgift där nån sa att om man inte kan hitta de exakta punkterna grafiskt är det bättre att lösa ekvationen algebraiskt. Jag försökte rita upp cirklarna för hand men det ger ju inte exakta punkter.
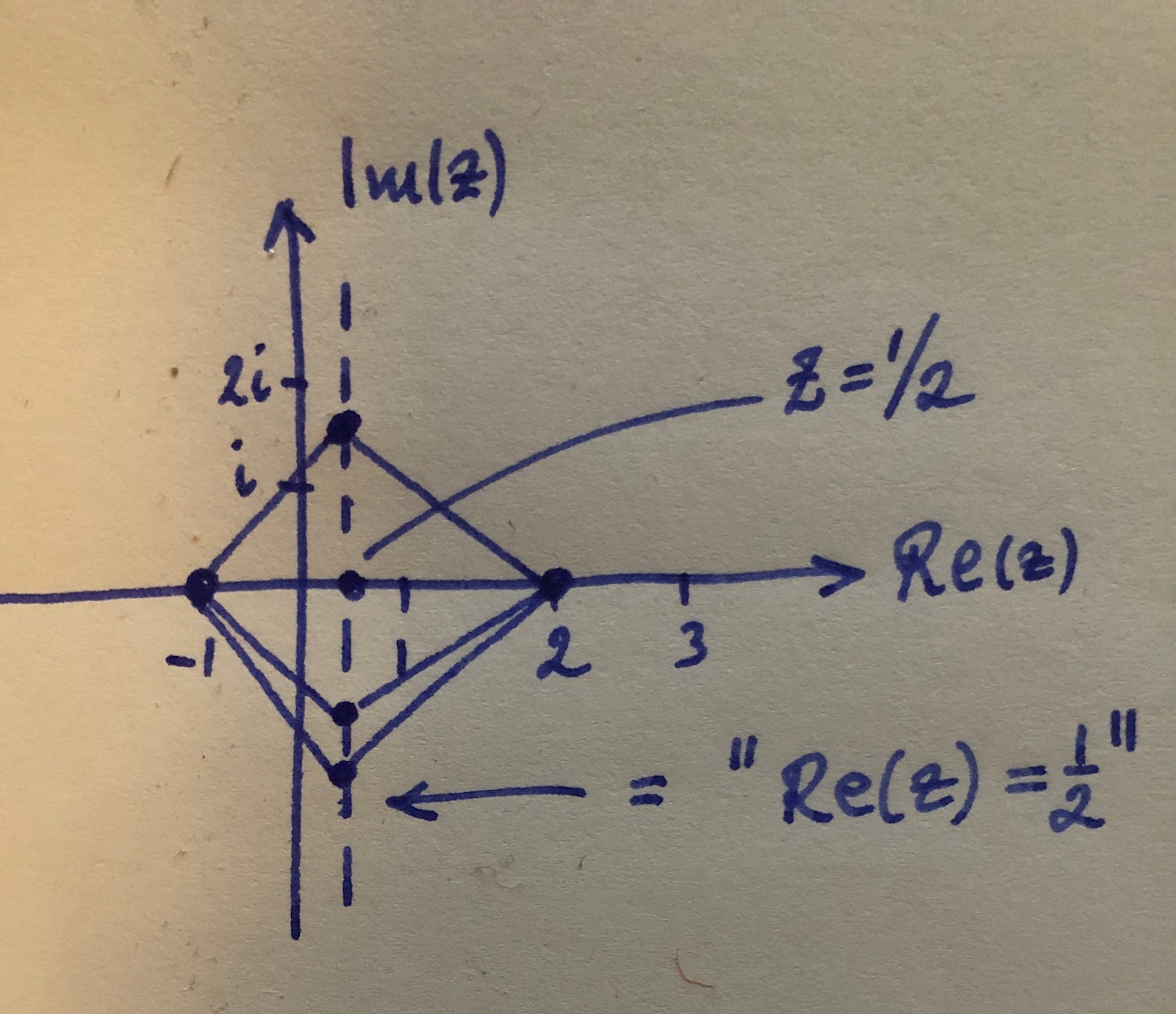
Se om du förstår denna grova skiss. Alla punkter på den lodräta linjen Re(z)=1/2 har lika långt till -1 som till 2.
Så egentligen är det 2-1/2=0,5.
Hur ska jag lösa b uppgiften? Där har jag i och ett reellt tal.
På samma sätt som ovan
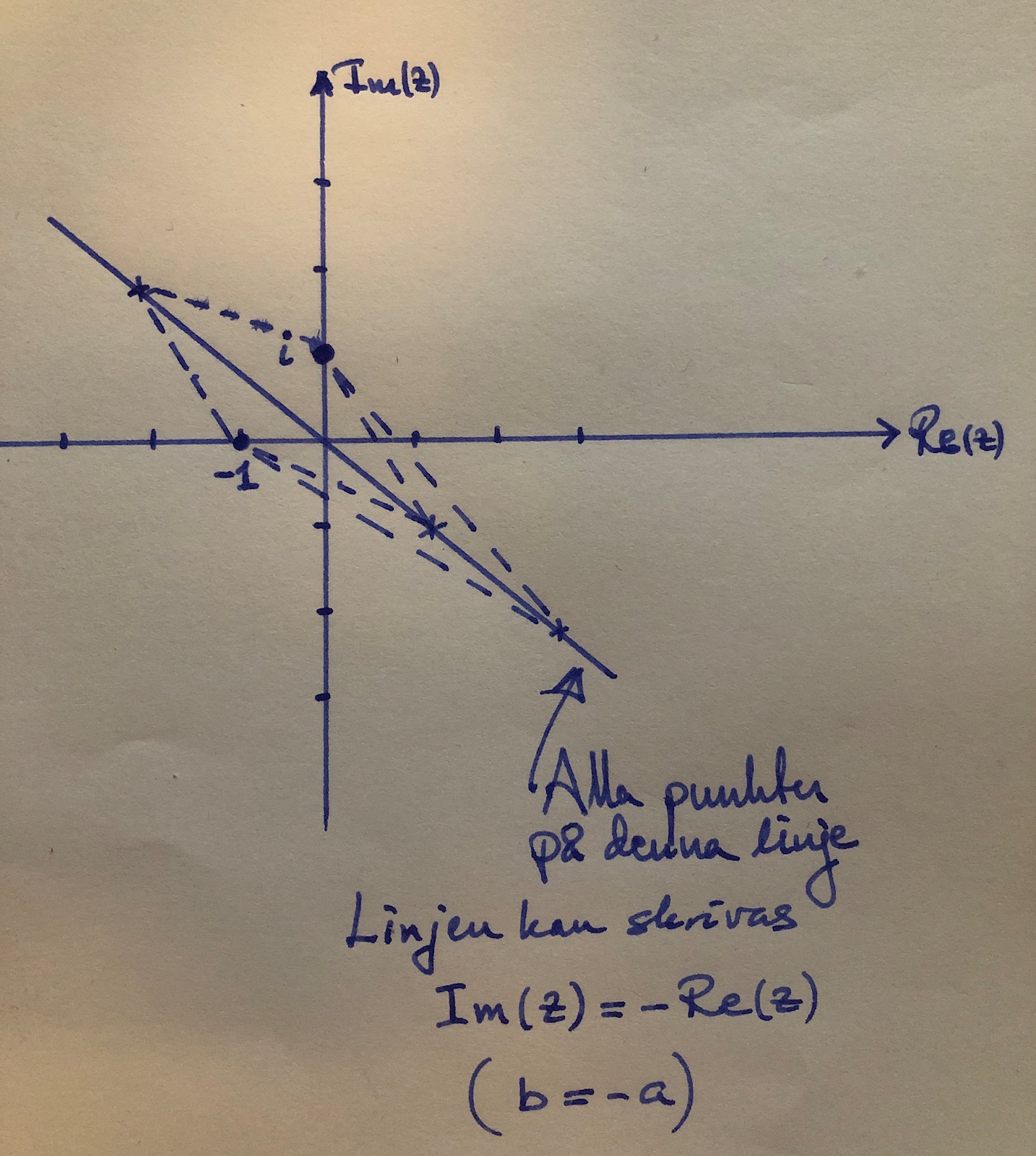
Jaha, så då tar jag och flyttar över Re z till det vänstra ledet och sätter 0 på det högra.
Då gjorde jag nästan rätt när jag försökte räkna ut det algebraiskt.
Föredrar du att räkna algebraiskt eller grafiskt för dessa uppgifter?
Hejsan266 skrev:Jaha, så då tar jag och flyttar över Re z till det vänstra ledet och sätter 0 på det högra.
Då gjorde jag nästan rätt när jag försökte räkna ut det algebraiskt.
Föredrar du att räkna algebraiskt eller grafiskt för dessa uppgifter?
Dessa lämpar sig bra för grafisk lösning.
Ja, Re(z)+Im(z)=0 är en bra formulering.
När det står att man skall markera alla punkter i det komplexa talplanet så måste man rita.


