Komplexa tal som vektorer
Jag kan för allt i världen inte förstå mig på hur ett komplext tal kan vara en vektor. Jag har suttit fast med det här i nästan en vecka så jag skulle verkligen uppskatta en grundläggande förklaring.
På vilket sätt sitter du fast? Har du en uppgift?
Nej, jag förstår matten som måste göras däremot så fastnar jag på att jag inte förstår mig på varför man får göra en vektor av komplexa tal i det komplexa talplanet.
Välkommen till Pluggakuten!
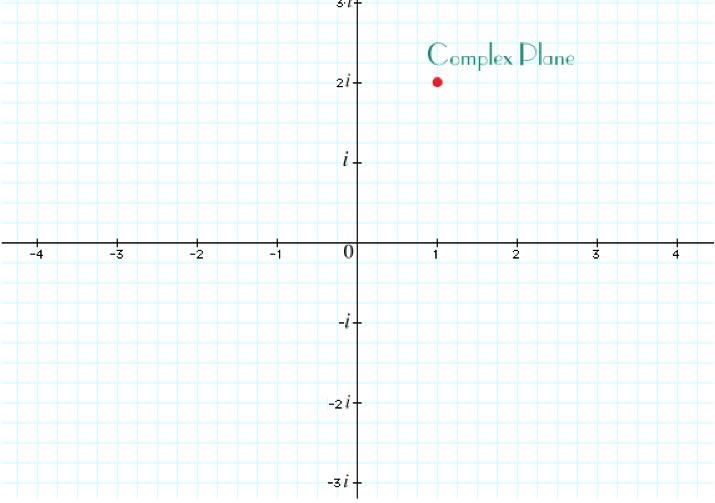
Kan du rita in t ex det komplexa talet z = 1+2i i det komplexa talplanet och lägga in bilden här?
Jag vet att det är så den ser ut, det jag inte förstår är varför man får göra en vektor när x och y axeln står för helt olika saker som inte går att addera.
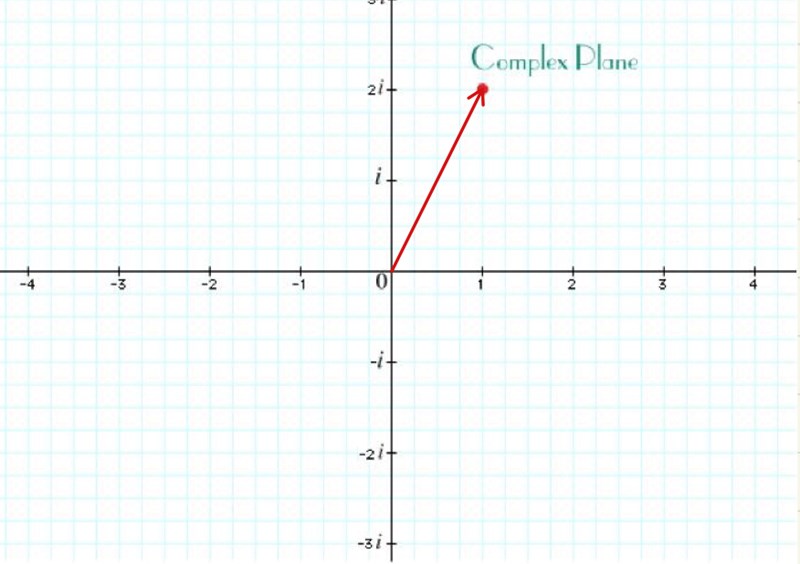
Vektorrepresentation är ett sätt att beskriva ett komplext tal med hjälp av ortsvektorn till aktuell punkt i komplexa talplanet. Detta ger en geometrisk bild av beloppet och argumentet (vinkeln mellan reella axeln och vektorn).
Det är en ren matematisk konstruktion som är mycket praktisk att använda. Polär form är ofta att föredra och är helt analogt med polära koordinater.
Jag föredrar att undvika att skriva i på imaginära axeln (många böcker gör det men jag tycker det är förvirrande). Om du tänker att det är imaginärdelen (Im z) av ett komplext tal som är "y-axeln" i komplexa talplanet så går representationen kanske ihop mer intuitivt=. Im z är ett ju ett reellt tal!
Matematiskt spelar det ingen roll dock.
Även i vanliga vektorer är väl x-axeln och y-axeln helt olika saker? Då pekar x-axeln åt ett håll och y-axeln åt ett annat. Och varför skulle man inte kunna addera t ex z1 = 1 och z2 = 2i?
Det som förvirrar mig är att på y-axeln står talen i formen n*i vilket enligt mig gör det ologiskt att man kan addera dem med reella tal när talen på y-axeln inte är reella.
Hur skulle man kunna addera 1+2i så att det blir något annat än det komplexa talet 1+2i? Det är därför jag inte förstår hur man kan få ett reellt absolutbeloop när x-axeln är reell och y-axeln är imaginär.
Man kanske ska fråga sig vad en vektor egentligen är, och vad som får kallas en vektor.
Ska jag vara ärlig så är jag väldigt dålig på vektorer eftersom vi aldrig arbetade med det i matte 1c.
Men min förståelse av en vektor är att den måste ha en riktning och en storlek som motsvaras av vektors längd. Där de olika komponenterna (x och y) som ger vektorns längd måste ha samma enhet. Vilket är varför jag inte förstår hur man skulle kunna addera längden på x-axeln med längden på y-axeln när y-axeln är imaginär.
Gör som Pelle föreslog och tänk dig att det som är på imaginära axeln är imaginärdelen, d v s 2 om z = 1+2i.
Man kan definiera rotationer och skalningar av sådana här komplexa vektor, genom multiplikation med ett komplext tal. Däremot får man något annat än skalärprodukten om man multiplicerar två komplexa vektorer.
Jag ber om ursäkt men det är fortfarande helt ologiskt för mig hur det går ihop att man kan få en reell längd, även om man ser på y-axeln som Imz där y är reellt så är det ju fortfarande tal som står för något helt annat. Ett steg på y-axeln är ju i medan ett steg på x-axeln är 1, jag förstår inte för allt i världen hur det går ihop att man kan få ett reellt avstånd från det.
När vektorer introduceras i skolan första gången så tar man inte upp allt som kan sägas om en vektor och i vilka sammanhang de kan användas. Prova att läsa t.ex. wikipedia-sidorna där vektor definieras, och se hur din nuvarande intuition stämmer med det som står där, och om det som står där går ihop med vektorer i komplexa talplanet.
https://sv.wikipedia.org/wiki/Vektor