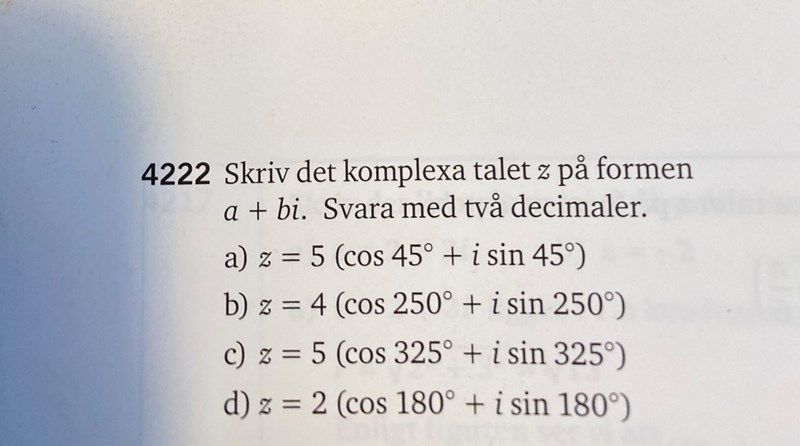komplexa talet z på formen a+bi

Det var länge sedan jag räknade med komplexa tal, men rent sporadiskt skulle ja bara göra såhär:

$\cos 45° =\hspace{0.17em}\sin 45° =\hspace{0.17em}\frac{1}{\sqrt{2}}$

$z=\frac{5}{\sqrt{2}}+\frac{5i}{\sqrt{2}}$

Om 

$z=5(\cos 45°+i\sin 45°)=\left(5*\cos 45°\right)+i*\left(5*\sin 45°\right)$

så borde 

$a=\left(5*\cos 45°\right)$

$b=\left(5*\sin 45°\right)$

Detta blir det du skrev, men 45 grader är en av de vinklar som finns som en identitet, så man kan svara med exakta värden. Jag vet inte vad uppgiften frågar efter.

Värdena för sin45^o och cos45^o är standardvärden som du väntas kunna utantill. Båda ä r lika med $\frac{\sqrt2}{2}$. Om det inte står i uppgiften bör du svara med ett exakt värde. Så det stämmer, men du har svarat på fel sätt.

okej så jag ska svara z=3,54+3,54i?

Nej du ska inte svara med ett närmevärde.

Faktum är att du inte behöver använda trigonometri alls för att lösa uppgiften.

Din metod att rita en rätvinklig triangel med hypotenusa 5 och vinkel 45° är en utmärkt idé.

Triangelns vinklar blir då 45°, 45° och 90°, vilket innebär att triangeln är likbent.

Kalla nu kateternas längd för $a$.

Pythagoras sats ger dig då helt enkelt att $a=\frac{5}{\sqrt{2}}$.

Eftersom triangeln är likbent så är både realdelen och imaginärdelen av $z$ lika med $a$.

Rätt svar är alltså $z=\frac{5+5i}{\sqrt{2}}$.

Svaret kan skrivas på ett flertal olika sätt, men det viktiga är att du har med $\sqrt{2}$ i svaret och att du inte svarar med ett närmevärde. 

okej :) men i uppgiften frågar dem just efter att man ska svara på formen a+bi, hur blir det då isf?

Joh_Sara skrev:

okej så jag ska svara z=3,54+3,54i?

Nej, absolut inte, du skall ge ett exakt svar, d v s (i det här fallet) ett svar som innehåller $\sqrt2$.

EDIT: När det står i uppgiften att man skall svara med två decimaler, är naturligtvis ditt svar helt rätt - men det gick inte att gissa från hur frågan var formulerad i ditt förstainlägg.

i facit på matteboken står det så? men okej så man ska jobba med enhetscirkeln för att få rätt?

Joh_Sara skrev:

okej :) men i uppgiften frågar dem just efter att man ska svara på formen a+bi, hur blir det då isf?

Kan du ladda upp en skärmdump av uppgiften?

Joh_Sara skrev:

Tack så mycket, det här förenklar att förstå uppgiften.

Börja med att multiplicera in femman. Du har nu:

$z=5 \times \cos 45° + 5\times i \sin 45°$

Du kan nu använda miniräknaren för att multiplicera ihop 5 och cos 45 samt 5 och sin 45. Avrunda till två decimaler.

ja men då blir det som jag skrev i mitt första inlägg.

$$\begin{gathered} 5*\cos 45\approx 3,535=3,54 \\ 5*\sin 45\approx 5,535=3,54 \end{gathered}$$

men sedan med enhetscirkeln förstår jag inte riktigt hur jag ska göra eller läsa av, vid 45 grader så är ju cos=$\frac{\sqrt{2}}{2}$och sin= $\frac{\sqrt{2}}{2}$

det blir samma svar (värde) på cos och för sin för att dem har samma vid 45 grader? eller är jag helt ute och cyklar.

Har löst dem andra uppgifterna på samma sätt, att jag multiplicerat cos250 med 4 och sin250 med 4 för att få fram sidorna. 

Du har med andra ord gjort helt rätt.

Du har gjort rätt.

För en börja med att lära sig enhetscirkeln kan det vara bra att läsa på de olika regelerna som finns för samband mellan cos, sin och tan. Dem kan du hitta här: https://www.formelsamlingen.se/media/2019302/formelblad_matematik_5.pdf

Sedan för att få en djupare förståelse; Jag lärde mig att använda enhetscirkeln genom att studera de olika värdena på cos, sin och tan i olika vinklar.

Kryssa i alla rutorna och dra i cirkeln uppe till vänster, studera sedan värdena på cos, sin och tan för olika vinklar. 

https://www.geogebra.org/m/cNEtsbvC

tack för all hjälp. Toppenbra! :)