komplexa talplanet
Markera i det komplexa talplanet de komplexa tal zzför vilka det gäller att ∣z−(3+3i)∣=∣z+(1+i)∣.
Jag har bara ritat in 3+3i och 1+i men jag vet inte hur jag ska fortsätta.
Sådana tal ligger på en linje som är vinkelrät mot linjen mellan punkterna och delar den linjen mitt av, d v s en linje som går genom (1,1) och har lutningen -1. I parameterform z = t + i(2-t).
bolibompa skrev:Markera i det komplexa talplanet de komplexa tal zzför vilka det gäller att ∣z−(3+3i)∣=∣z+(1+i)∣.
Jag har bara ritat in 3+3i och 1+i men jag vet inte hur jag ska fortsätta.
Det är dessa två punkter som du borde ha ritat in: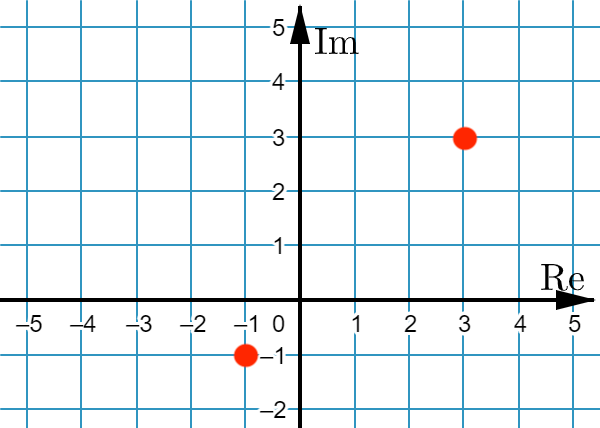 Sedan kan man fortsätta med hitta ställen sam har samma avstånd till dessa två punkter.
Sedan kan man fortsätta med hitta ställen sam har samma avstånd till dessa två punkter.
Pieter Kuiper skrev:bolibompa skrev:Markera i det komplexa talplanet de komplexa tal zzför vilka det gäller att ∣z−(3+3i)∣=∣z+(1+i)∣.
Jag har bara ritat in 3+3i och 1+i men jag vet inte hur jag ska fortsätta.
Det är dessa två punkter som du borde ha ritat in:
Sedan kan man fortsätta med hitta ställen sam har samma avstånd till dessa två punkter.
Blir det som en rät linje då? och vad gör det för skillnad om den är addaerat med z eller subtraherat?
Bra fråga. Det står minus på ena stället i uppgiften och plus på det andra. Det som ger avståndet mellan z och a är |z-a|, så vi får göra om uttrycket som har plus.
|z + (1+i)| = |z - (-1-i)|.



