komplexa talplanet
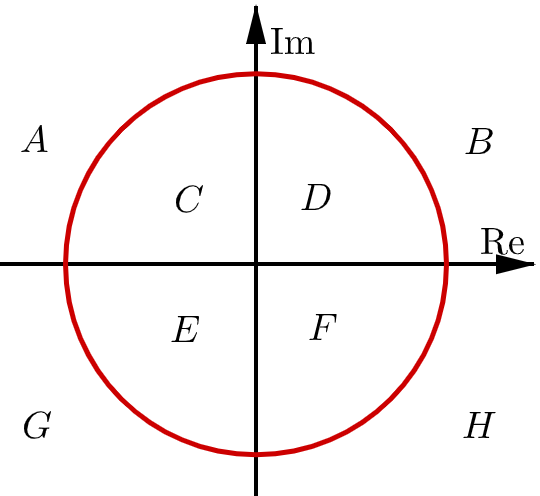I figuren är åtta olika områden i det komplexa talplanet markerade med A, B, C, D, E, F, G och H. Cirkeln är en enhetscirkel med centrum i origo. Cirkeln och koordinataxlarna ingår inte i något av de markerade områdena. Bestäm i vilket eller vilka områden talet 1/z kan ligga om z ligger i B.
Jag får fram att den ska vara mellan 0 och -90 grader men jag förstår inte hur jag ska avgöra om det är f eller h
Du behöver bara ett tal för att avgöra det. Till exempel z = 2 + 2i.
Pieter Kuiper skrev:Du behöver bara ett tal för att avgöra det. Till exempel z = 2 + 2i.
men det ska ju gälla för alla tal väl?
För z i B gäller |z|>1 varvid |1/z|<1 (det framgår inte ifall områdena innehåller sin tand eller ej, så jag tar det konsekvent utan rand). Det betyder att vi måste hamna innanför enhetscirkeln. Konjugatkompletterar vi 1/z och sätter z=a+ib får vi 1/z =(a-ib)/(a2+b2). Nämnaren är positiv och påverkar därför inte uttryckets tecken. Nu kan du läsa av var vi hamnar genom att titta på tecknen på a och b när z ligger i området B.
Tomten skrev:För z i B gäller |z|>1 varvid |1/z|<1. Det betyder att vi måste hamna innanför enhetscirkeln.
Ja, och det var det som behövdes för att avgöra TS:s fråga om hur man kunde avgöra mellan F och H.
