komplext tal

Det är för att jag kollar på mitt formelblad som säger att tan (-1) = 135°

Men mitt vinkelvärde bör ligga i 3 kvadranten och därmed vara 225° (315° menar jag)

Man kan alltså inte tänka som vanligt med vinklarna då

Får se nu... vi får använd de Movires formel.

$-1+\sqrt{3}i$ger ett absolutbelopp på 2, ett argument på -pi/6.

$1-i$ger ett absolutbelopp på 2^0,5, ett argument på -pi/4.

Detta ger

$\frac{{\left|2\right|}^6*e^{-i{\displaystyle \frac{\pi }{6}}*6}}{{\sqrt{2}}^9*e^{-i{\displaystyle \frac{\pi }{4}}*9}}=2^{6-9/2}*e^{-i\pi -i\frac{9}{4}\pi }=2^{3/2}*e^{-i\pi 5/4}$

Vad var det du fick? Du har skrivet tre olika vinklar(pi/4, 135^o och 225^o).

Jag får det till att -1+sqrt3i är 2pi/3 och att 1-i är 7pi/4.

Förstår inte Eulers formel

Jag får

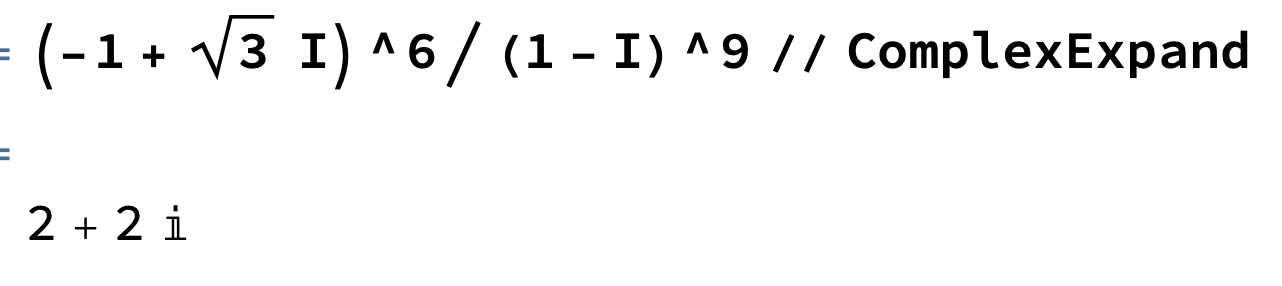
Hur gör man då 

Okej tack 🙂

Men hur går förenklingen till med att sqrt2^9 är samma som 2^4 sqrt2?

Dkcre skrev:

Okej tack 🙂

Men hur går förenklingen till med att sqrt2 är samma som 2^4 sqrt2?

Jag antar att det är denna sekvens du undrar över?

Första likheten: Nämnaren $(\sqrt{2})^9=(2^{1/2})^9=2^{1/2\cdot9}=$

$=2^{9/2}=2^{8/2+1/2}=2^{4+1/2}=$

$=2^4\cdot2^{1/2}=2^4\sqrt{2}$

Andra likheten: Förkorta bråket med $2^4$

Tredje likheten: Förlång bråket med $\sqrt{2}$ och förkorta sedan med $2$

Blev det tydligare då?

Dkcre skrev:

[...]

Förstår inte Eulers formel

Menar du de Moivres formel?

Läs i så fall om den här och fråga sedan oss om allt du vill att vi förklarar närmare.

Det blev tydligare. Men tur jag frågade, hade inte klurat ut det där själv, många steg att lyckas med.

Nej menar Eulers, det är väl den han använder längst ned där med exp funktionen..

Dkcre skrev:

Det blev tydligare. Men tur jag frågade, hade inte klurat ut det där själv, många steg att lyckas med.

Med träning så kommer du att göra det.

Nej menar Eulers, det är väl den han använder längst ned där med exp funktionen..

Jag är osäker på exakt vilken del av vilket svar du menar här. Kan du ladda upp en screenshot?

=======

Eulers formel beskriver ett samband mellan komplexa tal skrivna på exponentiell  polär form och trigonometrisk polär form:

$e^{iv}=\cos(v)+i\cdot\sin(v)$

Vad är det med den som du undrar över?

Kanske. Vi får se.

Var helt rimligt när jag såg det du gjort, men har i stort sett ingen aning om vad jag ska göra nu när jag försökte göra det själv. Det är konstigt men så är det, tittar på siffrorna liksom och dom säger ingenting för mig, är bara en massa symboler på ett papper. Kan inte ens förklara problemet, jag fattar bara inte.

Inget än så länge, ska gå igenom formeln sen i boken här så får ta den då.. :)