Komposanter och multiplikationstabell

Hej! Jag bara undrar om den bästa förklaringen till varför Ax=A*i etc är denna:
A=Axi+Ayj+Azk
Ax=A*i=(Axi+Ayj+Azk)*i= Axi*i+Ayj*i+Azk*i
Sen kollar vi på tabellen (till vänster för skalärprodukt) som jag inte hittar någon nytta av än just det här problemet. Lol, jag förstår fortfarande inte varför dessa tabeller är viktiga så jag har valt att inte memorera dem.
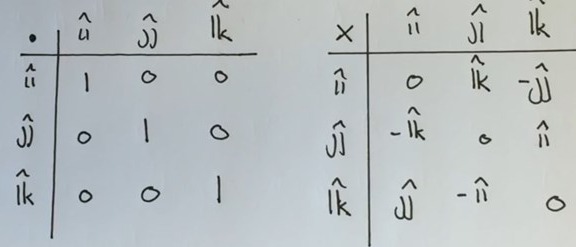
Så utifrån den vänstra tabellen är:
i*i = 1
i*j = 0
i*k = 0
Alltså är:
Ax= Ax*1+Ay*0+Az*0=Ax
Alltså det är inte någon trigonometri eller projektion till varför Ax=A*i, det är bara substituering?
En godtycklig vektor, i ditt fall A, har projektionen A * i (skalärprodukt) på en godtycklig enhetsvektor i.
Så det är en projektion. Och givetvis är i * j = 0, och i * k = 0
Gunnar_ skrev:En godtycklig vektor, i ditt fall A, har projektionen A * i (skalärprodukt) på en godtycklig enhetsvektor i.
Så det är en projektion. Och givetvis är i * j = 0, och i * k = 0
Du jag försökte använda projektionsformeln för A på i för att få Ax men jag kunde inte riktig få fram det på samma sätt till det (Att Ax=A*i genom projektionsformeln). Så jag fick istället .

Ditt ursprungliga bevis är helt korrekt. Varför krångla till det?
PATENTERAMERA skrev:Ditt ursprungliga bevis är helt korrekt. Varför krångla till det?
Jag tänker bara att man borde känna till de flesta sätten att bevisa det så att man kan gå vidare... idk, du har rätt.


