Komposantuppdela magnetfältet
Hej! Jag blir väldigt förvirrad av b-uppgiften.
Uträkningen i facit ser bra ut enligt mig. Men hur skulle man göra om man ville låta magnetfältet stå som det är, och komposantuppdela de andra vektorerna i stället?
För att allt ska bli vinkelrätt så behöver både strömmen och ledarens längd komposantuppdelas. Men om man ska komposantuppdela båda två så får man ju dubbel faktor sin 60° × sin 60° vilket ger ett annat svar än facit.
Hur tänker jag fel?
"FBI" gäller när det är räta vinklar. Eftersom B och I inte är vinkelräta måste du beräkna hur stor den vinkelräta komposanten av B är.
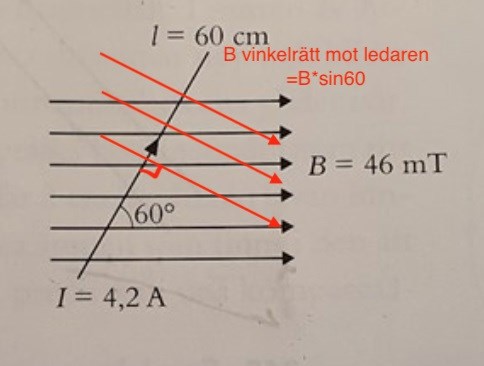
De röda pilarna är det vinkelräta fältet.
Ser du att du inte behöver göra något med strömmen? Nu är ju B och I vinkelräta.
Eftersom fältet från ledaren finns i "cirklar" runt ledaren är det svårare att tänka hur man skulle räta upp den.
Jag förstår det du skriver, men min fråga är: Hur gör man om man vill komposantuppdela allt förutom B-fältet?
D.v.s. att man komposantuppdelar strömmen och ledarens längd så att dessa blir vinkelräta mot B-fältet.
Detta leder ju till att man måste lägga till faktorn sin 60°, två gånger. En gång för att komposantuppdela strömmen och en gång för att komposantuppdela ledarens längd. Men som vi sagt så skulle det bara finnas en enda faktor sin 60°. Varför blir det fel när man tänker på det andra sättet?
Skillnaden blir:
F = B I l sin 60°
och
F = B I l sin 60° sin 60°
Så här tänker jag:
Vi vet att ledaren går i ett fält och ersätter vi den med en kortare vinkelrät längd har vi kompenserat för vinkeln.
Vi vet att strömmen går i ett fält och ersätter vi den med en lägre vinkelrät ström har vi kompenserat för vinkeln.
Att göra båda är att kompensera två gånger.
