Konfidensintervall, t-intervall

Jag känner inte riktigt igen att man ska ha med (N-a), och jag vet inte vad det skulle kunna betyda. 

Det jag är van att se är att du inte har med (N-a), och att det står ett + inne i roten. I sådana fall känner jag igen formeln som ett konfidensintervall för skillnaden mellan två gruppers medelvärde när de antas ha samma, men okända, standardavvikelse. Och i det fallet är s ”pooled sample standard deviation”.

Det ska vara ett + inne i roten - slarvfel av mig.

Dvs

$I_{\mu_i - \mu_j} = \bar y_i - \bar y_j \pm t_{\alpha /2} \cdot (N-a) \cdot s \cdot \sqrt{\frac{1}{n_i} + \frac{1}{n_j}}$

Sticksprovsgrupperna har olika, men kända, medelvärde och standardavvikelse.

Vad är det du vill göra konfidensintervall för? Vadå "deras konfidensintervall"? Formulera det tydligt först.

Du tycks ju använda formeln för konfidensintervall för skillnaden i väntevärde mellan två stickprov. Men du har ju tre stickprov. Prova red ut lite mer noga vad du vill göra först.

Sen är nog (N-a) antal frihetsgrader med avseende på t-fördelningen, inte en faktor. Sen måste ju a vara 2. Annars begriper jag inte vad målet är...?

Pompan skrev:

Det ska vara ett + inne i roten - slarvfel av mig.

Dvs

$I_{\mu_i - \mu_j} = \bar y_i - \bar y_j \pm t_{\alpha /2} \cdot (N-a) \cdot s \cdot \sqrt{\frac{1}{n_i} + \frac{1}{n_j}}$

Sticksprovsgrupperna har olika, men kända, medelvärde och standardavvikelse.

Okej, nu blev jag lite mer förvirrad. Medelvärden och standardavvikelse är kända? Vad är det du försöker göra ett konfidensintervall för? Jag håller med Daniel ovan, du måste skriva ned tydligare vad det är du försöker göra

Jag ska uppskatta de förväntade värdena $\mu_A$, $\mu_B$, $\mu_C$ genom att använda intervall så att den simultana konfindensintervallnivån $\alpha_{sim} \geq 94$

Jaha nej jag tror kanske jag ser (ett av) mina fel nu. Jag ska nog börja med att ställa upp detta för vardera stickprovsgrupp, dvs:

$I_\mu_i = \bar y_i \pm t_{\alpha/2} (N-a) \cdot s \cdot \sqrt{\frac{1}{n_i}}$

Ser det mindre orimligt ut?

En bild kanske hjälper:

$\bar y_i$ och $s_i$ för A verkar dock vara felskrivna (borde vara 52 resp. 18.34).

Okej, så du ska börja med att göra ett konfidensintervall för medelvärdet för varje grupp. Och eftersom även standardavvikelsen är okänd (alltså populationens standardavvikelse $\sigma$ är okänd, men de har gett dig stickprovens standardavvikelse s) använder du t-fördelningen.

Jag håller med Daniel att du nog har skrivit lite fel, (N-a) ska inte vara ett tal du multiplicerar med, utan det syftar bara till antalet frihetsgrader i t-fördelningen (så det är alltså t upphöjt till N-a eller något sådant). Och a är 1, N är storleken på stickprovet, alltså 6, 10 och 5. 

Okej! Ja, jag rörde till det lite där.

Att (N-a) är antal frihetsgrader är jag med på, fick bara inte till mindre ( ) i föregående inlägg.

Dock hänger jag inte med på hur a är 1, och om N är storleken på stickprovet, vad är då $n_i$?

Jag tolkade det som att $N = \sum_{i=1}^a n_i$

För A tänker jag att det ska se ut något i denna stil, om jag använder de siffror du angav:

$I_\mu_i = \bar y_i \pm t_{\alpha/2} \left(N-a \right) \cdot s \cdot \sqrt{\frac{1}{n_i}} =$

$= 51.83 \pm t_{0.02/2} \left( 6 - 1 \right) \cdot 17.98 \cdot \sqrt{\frac{1}{6}} =$

Det är dock inte rätt, så min tolkning är fortfarande fel. Osäker på s, tror jag glömt nåt steg där.

Om du använt de siffror du skriver så har du letat efter fel värde för t. Du har skrivit att du ska göra ett 94-% konfidensintervall, så alfa är 0.06, och alfa/2=0.03 (nu har du tittat efter alfa=0.02)

Tillägg: 29 sep 2022 14:10

Eller ok, kanske är det inte 94-%, jag vet faktisk inte vad ”simultana” konfidensintervallnivån betyder så jag blir osäker här

Enligt mina anteckningar gäller (vid t-intervall-metod) att

Individuell konfidensnivå: $1-\alpha$

Simultan konfidensnivå: $1-\alpha_{sim} \geq 1-$ $a \choose {2}$ $\alpha$

Enligt

(Vilket är varför jag tänker att a måste vara minst 2)

Kravet är givet såhär:

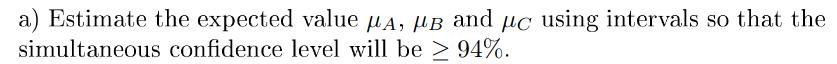
Okej, jag kan faktiskt inte svaret här

Okej, jag tror jag fått ihop det nu. Beräknade s på fel sätt förut. Om någon snubblar förbi tråden i framtiden så:

Saknade $s = \sqrt{\frac{SSE}{N-a}} = 22.4$

där N = 21 och a = 3

Har inte helt pejl på simultant/individuell konfidensnivå men väljer största möjliga $\alpha_{sim}$ (dvs) = 0.06 vilket ger $\alpha = 0.02$ och $t_{\alpha/2}(18) = 2.55$

Då kan man beräkna intervallet för en grupp som (B, $n_i = 10$)

$I_\mu_B = 82.2 \pm 2.55 \cdot 22.4 \cdot \sqrt{\frac{1}{10}}$

Sen är det tämligen enkelt att beräkna skillnaden mellan konfidensintervallen

$I_\mu_{A-B} = \bar y_A - \bar y_B \pm t_{\alpha/2} \left( N-a \right) \cdot s \cdot \sqrt{\frac{1}{n_A}+\frac{1}{n_B}}$

Med $t_{\alpha/2} \left(18\right)=2.55$ och $\alpha_{sim} \geq 0.94$ får man att $\mu_A <>$ men att det inte är någon skillnad mellan $\mu_A$ och $\mu_C$ eller $\mu_B$ och $\mu_C$.
Hur man kommer fram till detta fattar jag dock ej.

Tillägg: 29 sep 2022 20:29

Eller, är det för att intervallet A-B är nollskilt medan A-C och C-B ej är det?