Konservativt fält?

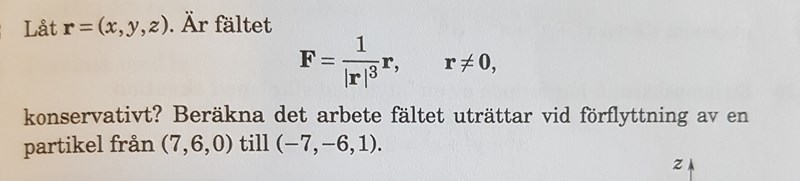
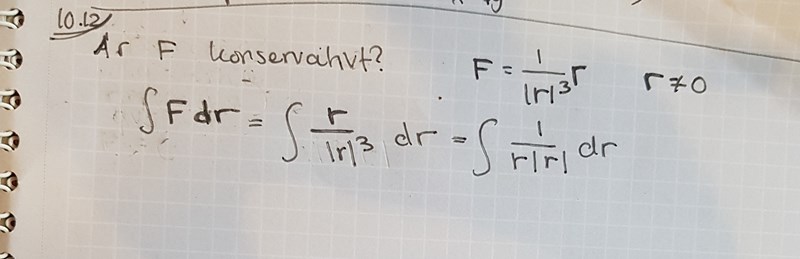
Ja, det här fältet är konservativt och dessutom beror det bara på avståndet till origo (r).

Fältet är konservativt eftersom $\mathbf{\nabla}\times \mathbf{F}=0$ i ett enkelt sammanhängande område $\Omega$.

Undersök därför om du kan finna en potential $U(r)$ som bara beror av avståndet till origo.

----------------------------------------------------------------------------------------------

En sak som förvirrade mig när jag började läsa om vektorfält är vilka villkor man ska ställa på området för att det ska anses vara tillräckligt regulärt.

Ett område $\Omega$ är enkelt sammanhängande om varje sluten kurva i $\Omega$ utan att lämna området kan deformeras kontinuerligt (längs en yta) till en punkt i $\Omega$.

I två dimensioner har man bara en yta att tillgå (xy-planet) och varje "hål" innebär att man inte längre kan krympa ihop en ögla utan att lämna området.

I 3 dimensioner är det mer komplicerat, där kan man ta bort en enskild punkt eftersom man kan kröka ytor "runt" men "tillräckligt nära" singulariteten. Det innebär t.ex. att $\mathrm{R}^3\setminus \{\mathbf{0}\}$ är enkelt sammanhängande.

Jroth skrev:

Ja, det här fältet är konservativt och dessutom beror det bara på avståndet till origo (r).

Fältet är konservativt eftersom $\mathbf{\nabla}\times \mathbf{F}=0$ i ett enkelt sammanhängande område $\Omega$.

Undersök därför om du kan finna en potential $U(r)$ som bara beror av avståndet till origo.

 

----------------------------------------------------------------------------------------------

En sak som förvirrade mig när jag började läsa om vektorfält är vilka villkor man ska ställa på området för att det ska anses vara tillräckligt regulärt.

Ett område $\Omega$ är enkelt sammanhängande om varje sluten kurva i $\Omega$ utan att lämna området kan deformeras kontinuerligt (längs en yta) till en punkt i $\Omega$.

I två dimensioner har man bara en yta att tillgå (xy-planet) och varje "hål" innebär att man inte längre kan krympa ihop en ögla utan att lämna området.

I 3 dimensioner är det mer komplicerat, där kan man ta bort en enskild punkt eftersom man kan kröka ytor "runt" men "tillräckligt nära" singulariteten. Det innebär t.ex. att $\mathrm{R}^3\setminus \{\mathbf{0}\}$ är enkelt sammanhängande.

Fattar tyvärt inte alls 😥

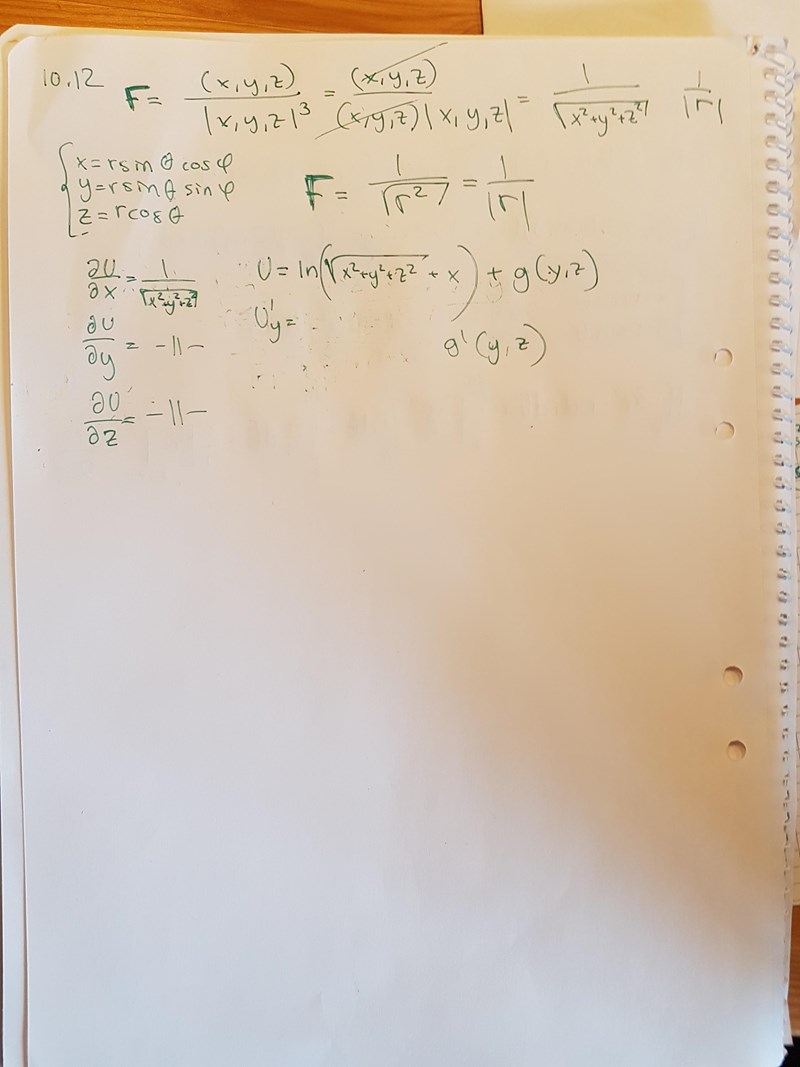
Försök alltså  finna potential U så att $\nabla U=\mathbf{F}$. Du har gjort ett försök men jag tror du halkade lite.

Börja med att sätta $U_x=\dfrac{x}{(x^2+y^2+z^2)^{3/2}}$ osv, på det sätt du försökte i din kalkyl.

dr_lund skrev:

Försök alltså  finna potential U så att $\nabla U=\mathbf{F}$. Du har gjort ett försök men jag tror du halkade lite.

Börja med att sätta $U_x=\dfrac{x}{(x^2+y^2+z^2)^{3/2}}$ osv, på det sätt du försökte i din kalkyl.

Tack!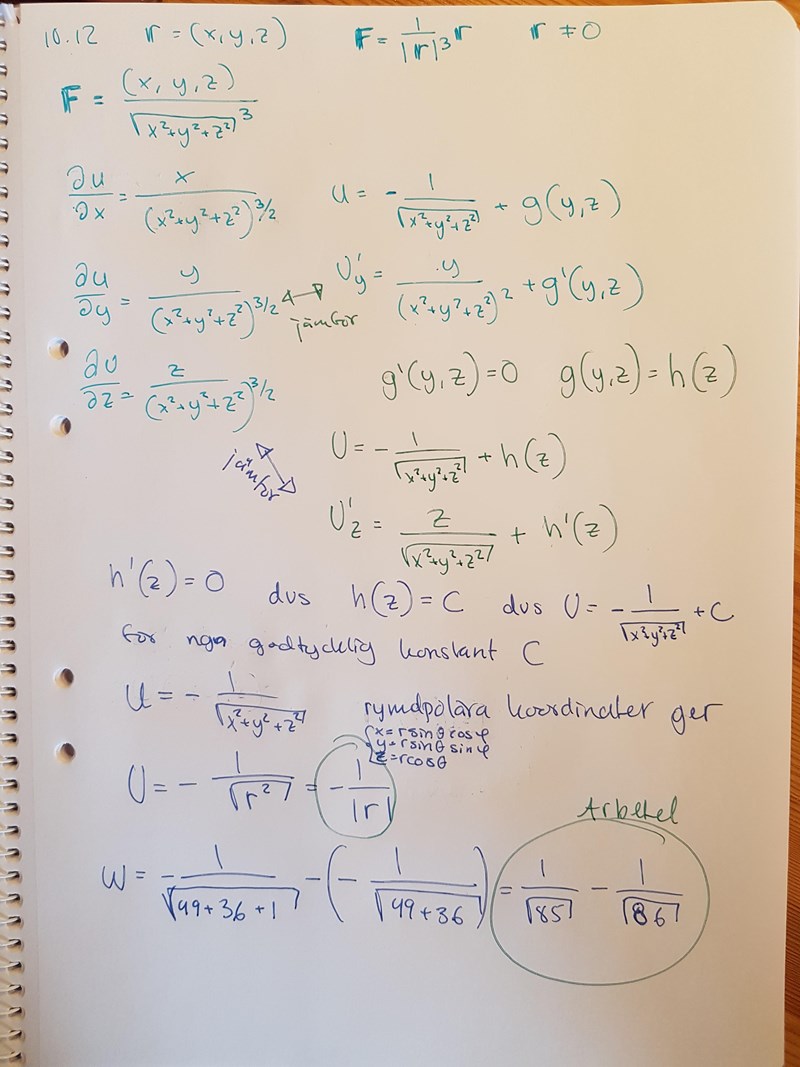

Om du vill kan du skriva om fältet redan från början

$\mathbf{F}(r)=\frac{r}{r^3}\hat{r}=\frac{1}{r^2}\hat{r}$

$\frac{\partial U}{ \partial r}=\frac{1}{r^2}\, \Rightarrow\, U(r)=-\frac{1}{r} +C$