Konstanten c
Hur hittar jag konstanten c i denna uppgift
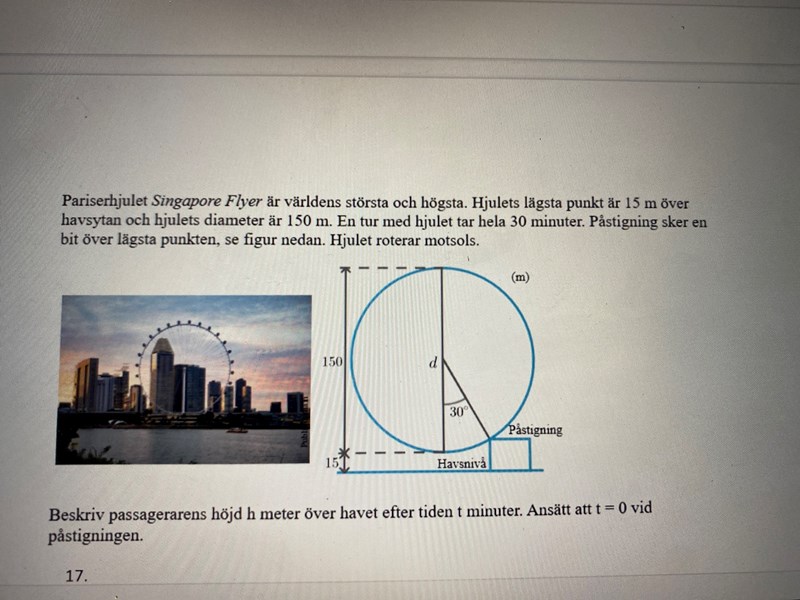
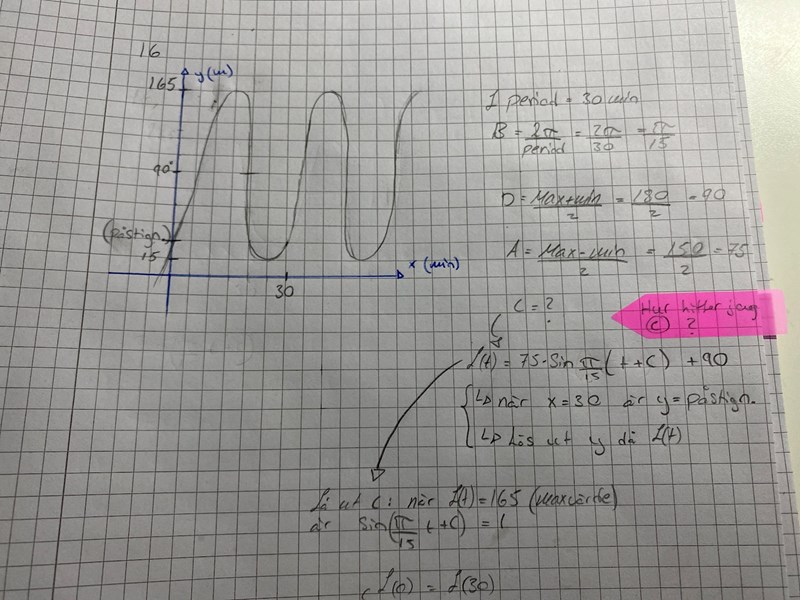
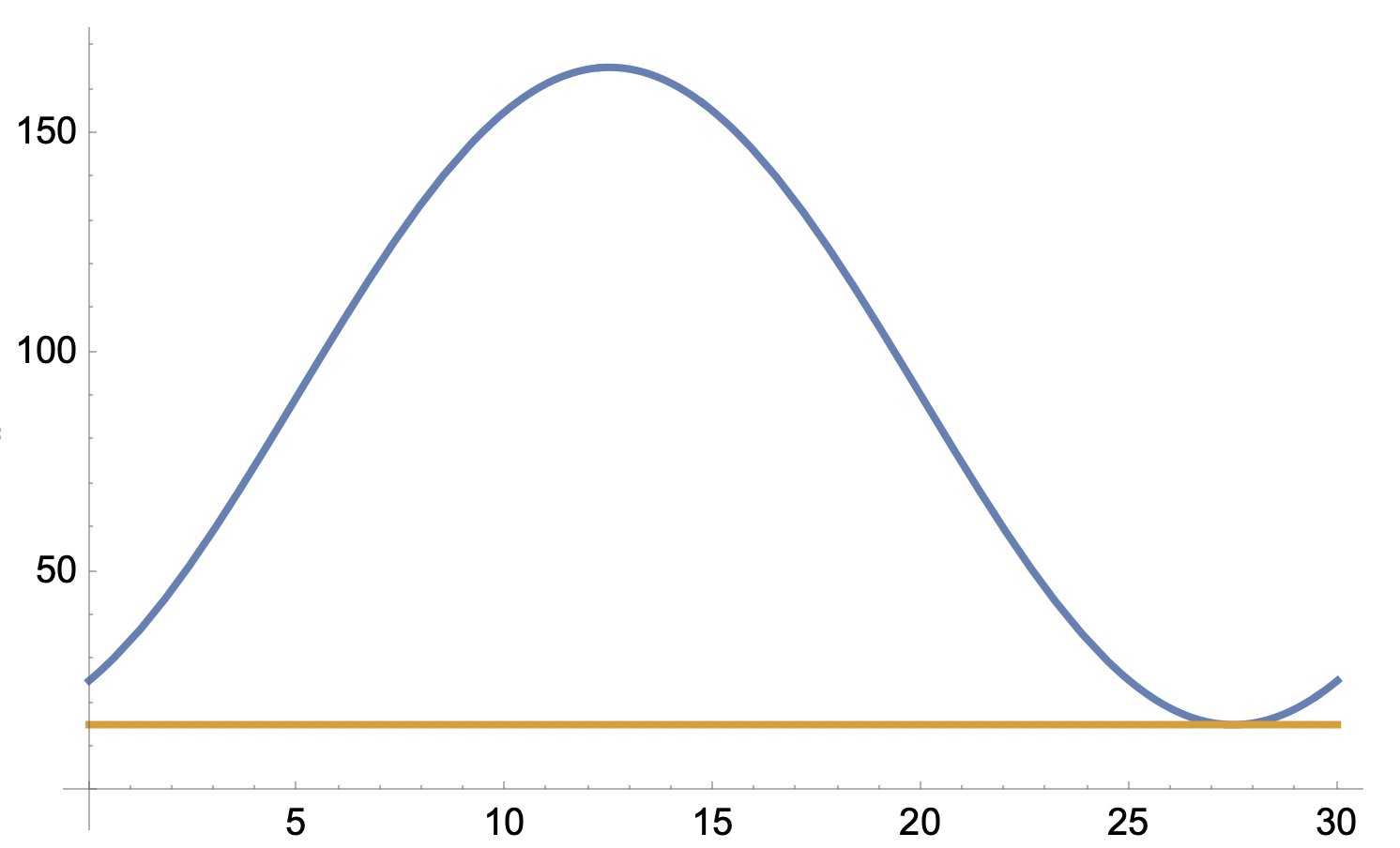
I normala fall vid påstigning på den lägsta punkten hade vi haft
y=75 sin(π/15 t) + 90
men:
1. Allt är vridet -π/2 mot normalt som vi måste räkna in
y = 75 sin(-π/2 + π/15 t) + 90
2. Start punkten är π/6 då t=0 vilket måste kompenseras
y = 75 sin(-π/2 + π/15 t + π/6) + 90 = 75 sin(π/15 t - π/3) + 90
(Vi kan även se startvinkeln som -π/3 vilket framgår av y = 75 sin(π/15 t - π/3) + 90)
Definitionsintervallet är 0≤t≤30.
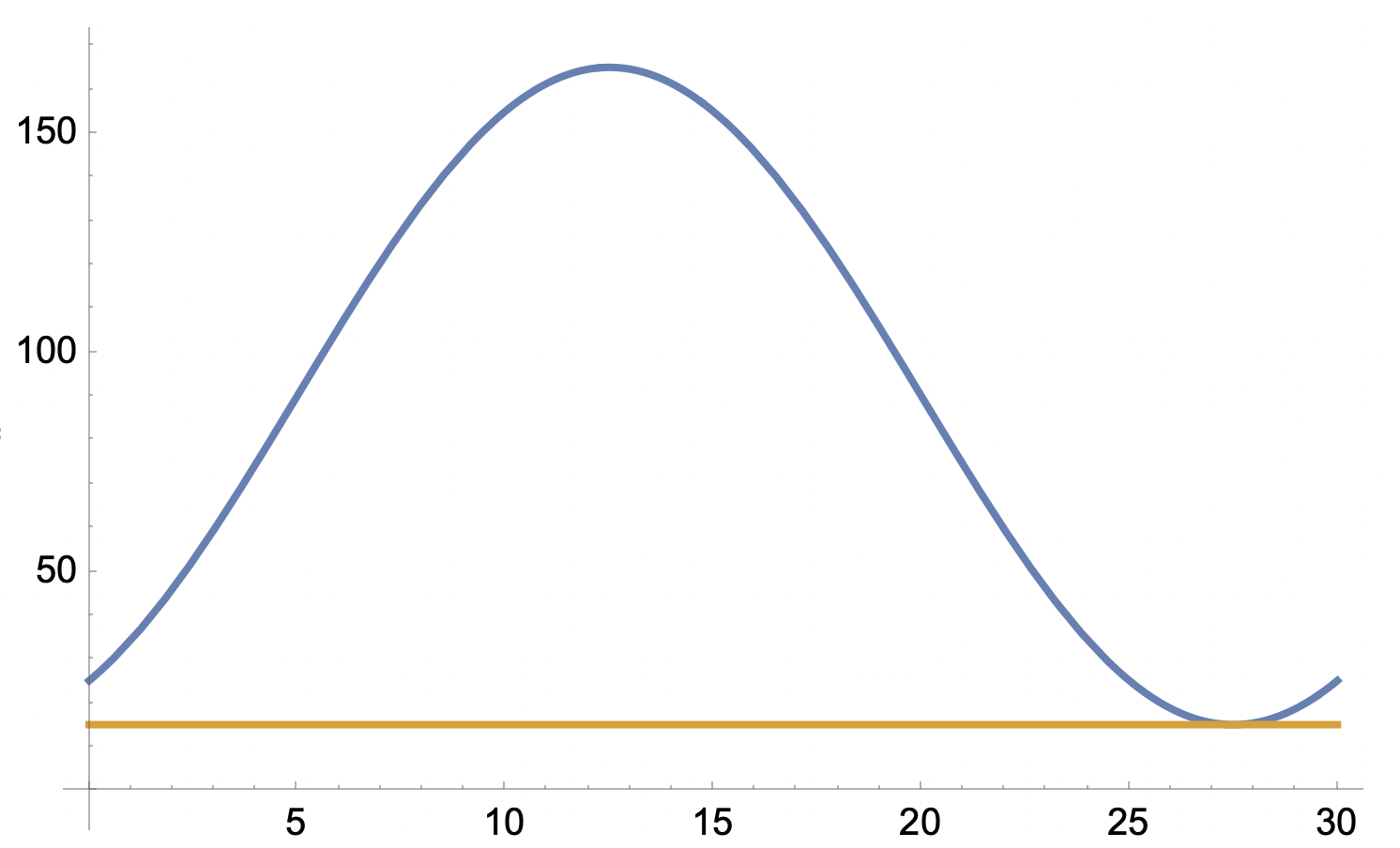
Trinity2 skrev:I normala fall vid påstigning på den lägsta punkten hade vi haft
y=75 sin(π/15 t) + 90
men:
1. Allt är vridet -π/2 mot normalt som vi måste räkna in
y = 75 sin(-π/2 + π/15 t) + 90
2. Start punkten är π/6 då t=0 vilket måste kompenseras
y = 75 sin(-π/2 + π/15 t + π/6) + 90 = 75 sin(π/15 t - π/3) + 90
(Vi kan även se startvinkeln som -π/3 vilket framgår av y = 75 sin(π/15 t - π/3) + 90)
Definitionsintervallet är 0≤t≤30.
vad menar du med att allt är vridet med -pi/2
Lolorahel skrev:Trinity2 skrev:I normala fall vid påstigning på den lägsta punkten hade vi haft
y=75 sin(π/15 t) + 90
men:
1. Allt är vridet -π/2 mot normalt som vi måste räkna in
y = 75 sin(-π/2 + π/15 t) + 90
2. Start punkten är π/6 då t=0 vilket måste kompenseras
y = 75 sin(-π/2 + π/15 t + π/6) + 90 = 75 sin(π/15 t - π/3) + 90
(Vi kan även se startvinkeln som -π/3 vilket framgår av y = 75 sin(π/15 t - π/3) + 90)
Definitionsintervallet är 0≤t≤30.
vad menar du med att allt är vridet med -pi/2
Sinusfunktionen (och pariserhjulet) utgår ofta från ett horisontellt noll-läge, x-axeln. Här börjar vi -90° (+30°)