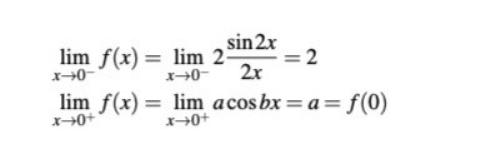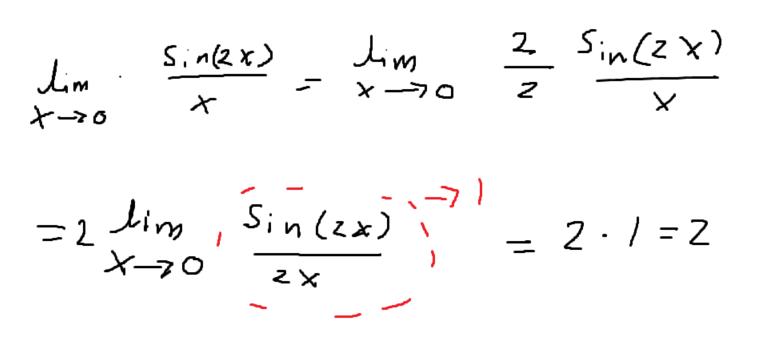kontinuerlig funktion
på första raden står det 2x i nämnare om man ersätter x=0 så blir ju nämnaren odefinerat hur fick dom 
Du kan inte bara stoppa in 0.
Men när x går mot 0, dvs är oändligt nära 0 så går den oänldigt nära 2. Om du stoppar in 0 rakt av så har du 0/0 vilket inte säger något om gränsvärdet.
Relatera detta till standardgränsvärdet du redan känner till om du låter så att du har:
när
Dracaena skrev:Du kan inte bara stoppa in 0.
Men när x går mot 0, dvs är oändligt nära 0 så går den oänldigt nära 2. Om du stoppar in 0 rakt av så har du 0/0 vilket inte säger något om gränsvärdet.
Relatera detta till standardgränsvärdet du redan känner till om du låter så att du har:när
Nej.
Du får alltså om du försöker stoppa in .
Dracaena skrev:Nej.
Du får alltså om du försöker stoppa in .
ja men hur fick dom 2 jag ser inte hur dom fick 2 efter dom lagt in x=0 i
Vad går hela uppgiften ut på?
Det ser ut som att det handlar om att vi skall försöka definiera funktionen så den är kontrinuerlig.
För f(0) så kan vi definiera det som f(0)=2, vilket tillför att funktionen nu är kontinuerlig men f(0) i sig är inte definierat. Men vi kan som sagt definiera ett värde så att f(x) är definierat överallt.
Vi har helt enkelt gjort detta:
Dracaena skrev:Vad går hela uppgiften ut på?
Det ser ut som att det handlar om att vi skall försöka definiera funktionen så den är kontrinuerlig.
För f(0) så kan vi definiera det som f(0)=2, vilket tillför att funktionen nu är kontinuerlig men f(0) i sig är inte definierat. Men vi kan som sagt definiera ett värde så att f(x) är definierat överallt.
Vi har helt enkelt gjort detta:
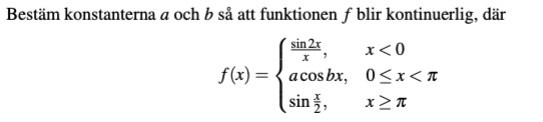
hur blev den till 2 vet du hur dom fick det till 2? förstår inte lösningen
Är du först och främst med på att om vi har
så är den diskontinuerlig i ?
Är du också med på att:
Är kontinuerlig?
Dracaena skrev:Är du först och främst med på att om vi har
så är den diskontinuerlig i ?
Är du också med på att:Är kontinuerlig?
ja jag är med men fattar inte hur dom fick det till 2..
Okej, bra. Nu vet vi att till höger så gäller det att vi slutar på (0,2). Precis som jag precis visade dig ovan, så är funktionen diskontinuerlig i . Okej, men från vänster går det mot 2. Det är ju bara att beräkna gränsvärdet, vilket är trivialt eftersom det är ett standardgränsvärde out of the box.
Ok, Nu måste alltså nästa bit börja där vi slutade. Så om vi slutar oändligt nära 2 från vänster, så måste vi börja oändligt nära 2 från andra sidan (högra sidan).
Förstår du nu denna biten?
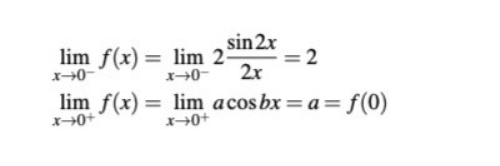
Samma resonomang gäller för den sista biten av funktionen.
Dracaena skrev:Okej, bra. Nu vet vi att till höger så gäller det att vi slutar på (0,2). Precis som jag precis visade dig ovan, så är funktionen diskontinuerlig i . Okej, men från vänster går det mot 2. Det är ju bara att beräkna gränsvärdet, vilket är trivialt eftersom det är ett standardgränsvärde out of the box.
Ok, Nu måste alltså nästa bit börja där vi slutade. Så om vi slutar oändligt nära 2 från vänster, så måste vi börja oändligt nära 2 från andra sidan (högra sidan).
Förstår du nu denna biten?
Samma resonomang gäller för den sista biten av funktionen.
skulle du kunna visa en snabbis hur man fick a=2 och b=1/3 ? jag förstår inte riktigt hur dom kom fram till det förstår inte riktig "förklaringar" är jätte tacksam om du kan visa med beräkning hur a=2 och b=1/2 på acosbx
Okej, jag ska försöka ge en mer involverad förklaring imorgon om ingen har gjort det redan som förhoppningsvis besvarar alla dina funderingar.
Ursäkta, har bara snabbläst, men det står inte att 2 sin(2x) /(2x) = 2 när x = 0.
Det står att gränsvärdet är 2 när x går mot 0.
Mogens skrev:Ursäkta, har bara snabbläst, men det står inte att 2 sin(2x) /(2x) = 2 när x = 0.
Det står att gränsvärdet är 2 när x går mot 0.
men hur fick dom 2 kan du visa en snabb beräkning snälla har en tenta vid lunch vill gärna förstå denna uppgift
Att sin v / v går mot 1 när v går mot noll (v i radianer) är säkert bevisat i läroboken om du ska kunna det.
Jag hoppas du hänger med så långt.
Detta betyder inte att sin(2x)/x är definierad i utan att det går mot det. Detta betyder i sin tur att om vi definierar att för så är värdet så har vi pluggat upp hålet. Precis som jag visade dig i inlägg #8 som du höll med om.
Vi vet att sin(2x)/x redan går mot 2, så nu måste vi se till att acos(bx) också går mot 2 när x går mot 0:
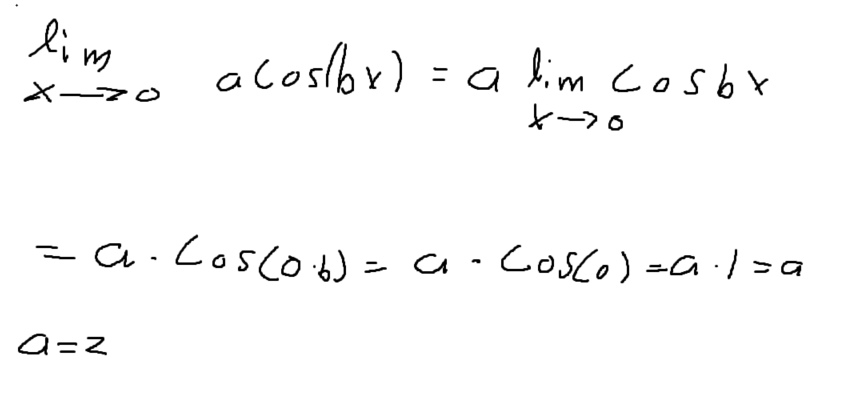
Hänger du med? När x går mo 0 så går acos(bx) mot a.
För att vi ska ha kontinuitet så måste alltså a = 2 för att acosbx måste börja där sin2x/x slutar, annars har vi ett hål.
Hänger du med?