Kontinuerliga funktioner?
Hej jag förstår inte riktigt uppgiften eller hur man ska lösa den

Om grafen är sammanhängande så ska du kunna rita den utan att lyfta på pennan.
Rita graferna till de olika funktionerna.
Kan du göra det utan att lyfta på pennan?
Om ja så är graferna sammanhängande och då är även funktionerna kontinuerliga.
Det är jag med på! Jag förstår bara inte Hur man ska använda de siffrorna och x-värdet för att få fram det. Vad betyder tex det som står inom klammern? Tillhör det samma funktion eller vad betyder de siffrorna. Samt, vad betyder det att det står 2st x värden till höger?
för alla x-värden mindre eller lika med 3
för all x-värden större än 3
Alltså kommer grafen först ha lutning 2x till x-värdet 3. Efter 3 kommer grafen ha värdet y=2.
Kurvan/grafen går alltså från lutning till plan om man kan uttrycka sig så.
Okej! Vad betyder 6an som står under tvåan? Och varför står det ett x värde bredvid 2x och ett x värde bredvid 6:an?
LukasEliasson skrev lite fel
f(x) = 2x för alla x-värden mindre eller lika med 3
f(x)= 6 för all x-värden större än 3
Okej! Jag förstår dock inte hur man ska använda siffrorna för att kunna se ifall det är en kontinuerlig funktion
Rita grafen! Om du kan rita grafen utan att lyfta pennan, dvs om den är utan "hopp", så är grafen sammanhängande. Om grafen är sammanhängande så är funktionen kontinuerlig.
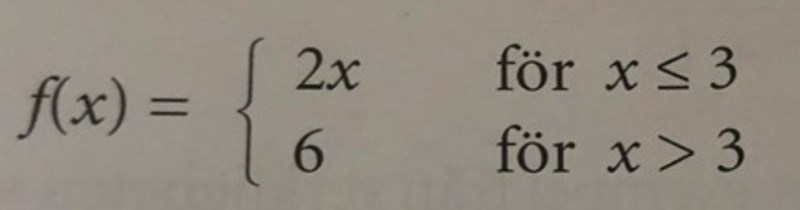
Grafen till denna funktion består av två räta linjer (egentligen två "strålar").
- Den ena linjen är y = 2x och den gäller för alla x3, röda delen av grafen i figuren.
- Den andra linjen är y = 6 och den gäller för alla x > 3, blåa delen av grafen.
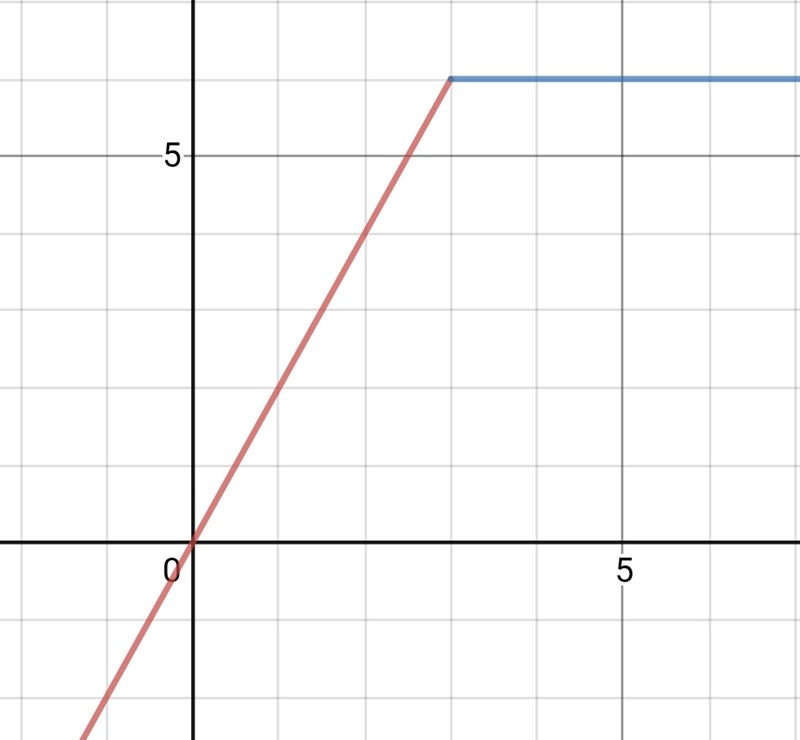
Skulle du kunna rita denna gtaf utan att lyfta pennan, dvs saknar den "hopp"?
I a-uppgiften är funktionen f(x) definieras om f(x)=2x om x är mindre än eller lika med 3 och f(x) = 3 om x är större än 3. Du skall avgöra om funktionen är kontinuerlig eller inte, d v s om det går att rita den utan att lyfta pennan.
Dvs om man kan rita hela den utan att lyfta pennan? Att man skriver in båda värdena och att de båda funktionerna som bildas ska man kunna rita tillsammans utan att lyfta pennan?
Tex den 3:e, om man skriver in båda h(x) så kan man inte rita de båda utan att lyfta pennan. Är det så?
Tindra skrev:Dvs om man kan rita hela den utan att lyfta pennan? Att man skriver in båda värdena och att de båda funktionerna som bildas ska man kunna rita tillsammans utan att lyfta pennan?
Ja det stämmer. Om du kan rita funktionens graf utan att lyfta pennan så är grafen sammnhängande och då är funktionen kontinuerlig.
Tindra skrev:Tex den 3:e, om man skriver in båda h(x) så kan man inte rita de båda utan att lyfta pennan. Är det så?
Ja det stämmer. Den grafen har ett "hopp" från y = 2 vid x = 1 ner till y = 1 strax till höger om x = 1.
Du kan inte rita hela funktionens graf utan att lyfta pennan. Grafen är inte sammanhängande. Funktionen är inte kontinuerlig.
Så på c) är den diskontinuerlig för att man inte kan rita båda dessa utan att lyfta pennan?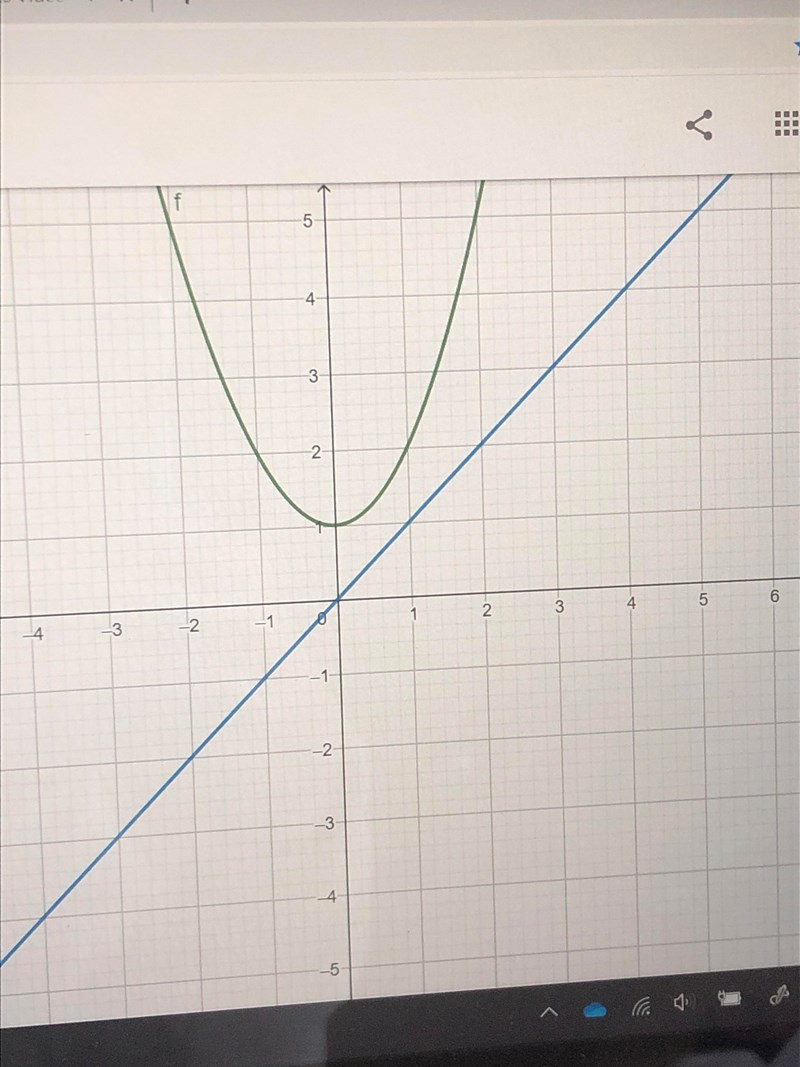
Ja det stämmer, men grafen stämmer inte riktigt. Den ska se ut så här. För varje värde på x så finns det alltså endast ett värde på y.
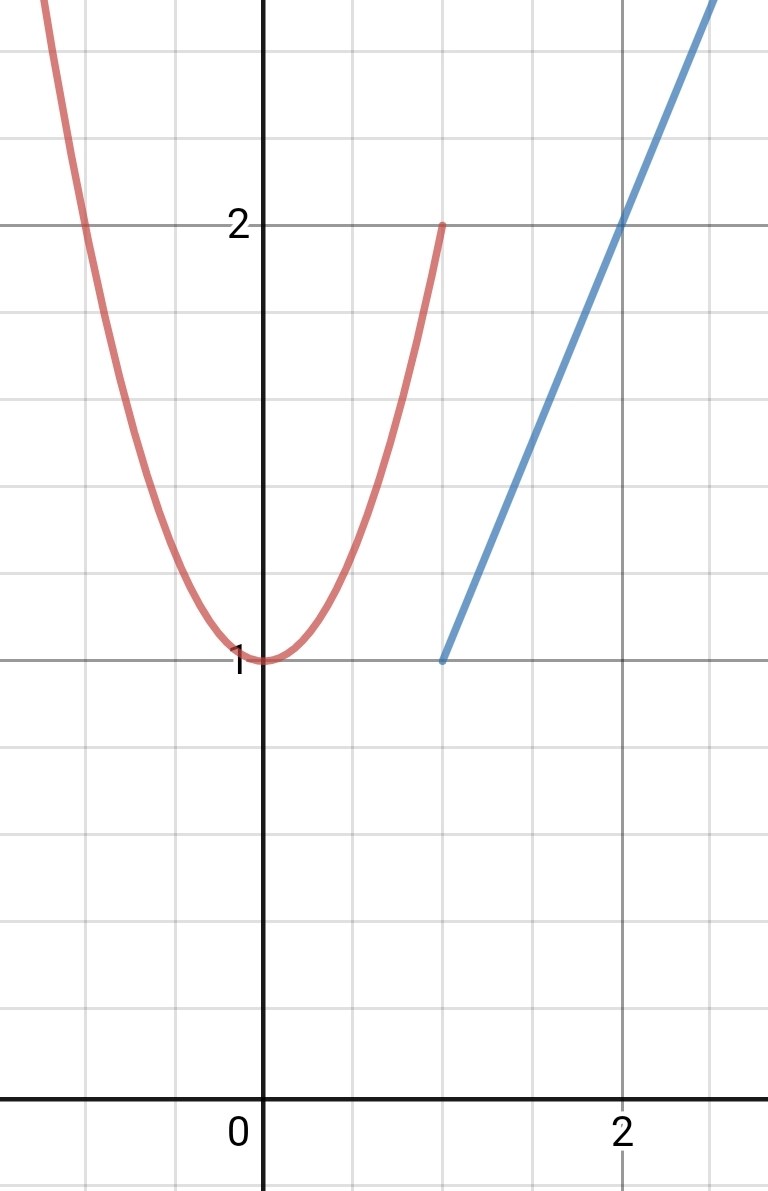
Den gröna kurvan gäller om x är 1 eller mindre. Den blåa kurvan gäller om x är större än 1. Det blir ett hopp när x = 1. Kurvan är inte kontinuerlig.
Okej tack för hjälpen allihopa!





