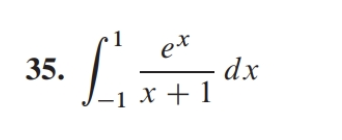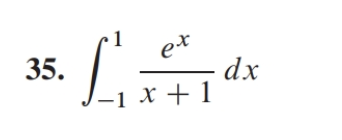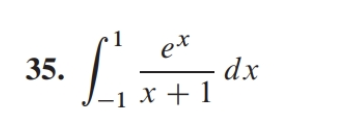konvergens eller divergens
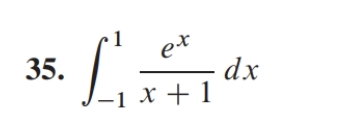
uppgiften går ut på att avgöra om integralen divergerar eller konvergerar. Vet dock inte hur jag ska tänka
Har du löst några liknande uppgifter förut?
Koizenu skrev:
uppgiften går ut på att avgöra om integralen divergerar eller konvergerar. Vet dock inte hur jag ska tänka
Vi kan inte lätt beräkna primitiv funktion så vi måste angripa den på något annat sätt. Kan vi "göra av" med e^x på något sätt genom att finna en undre begränsning för e^x på det givna integrationsintervallet?
Vi vill alltså skriva
INT_{-1}^1 e^x/(x+1) dx > INT_{-1}^1 C/(x+1) dx
där C är någon reell konstant.
Lasse Vegas skrev:Har du löst några liknande uppgifter förut?
Nej, men i boken står det att man ska kolla på en integral som liknar denna
Trinity2 skrev:Koizenu skrev:
uppgiften går ut på att avgöra om integralen divergerar eller konvergerar. Vet dock inte hur jag ska tänka
Vi kan inte lätt beräkna primitiv funktion så vi måste angripa den på något annat sätt. Kan vi "göra av" med e^x på något sätt genom att finna en undre begränsning för e^x på det givna integrationsintervallet?
Vi vill alltså skriva
INT_{-1}^1 e^x/(x+1) dx > INT_{-1}^1 C/(x+1) dx
där C är någon reell konstant.
Ska vi då hitta C
Koizenu skrev:Trinity2 skrev:Koizenu skrev:
uppgiften går ut på att avgöra om integralen divergerar eller konvergerar. Vet dock inte hur jag ska tänka
Vi kan inte lätt beräkna primitiv funktion så vi måste angripa den på något annat sätt. Kan vi "göra av" med e^x på något sätt genom att finna en undre begränsning för e^x på det givna integrationsintervallet?
Vi vill alltså skriva
INT_{-1}^1 e^x/(x+1) dx > INT_{-1}^1 C/(x+1) dx
där C är någon reell konstant.
Ska vi då hitta C
Ja. Rita e^x på [-1,1] och se vad du kan säga om e^x.
Så hä kanske? Låt f vara integranden. Då är f kontinuerlig utom för x=-1 och f>=e-1 • 1/(x+1) i integrationsintervallet,. Tag r tillhörande -1<r<0. I detta intervall är |Int(f)|>= e-1 •|ln 1-ln (r+1)|—> oändl när r—>0. I intervallet 0<=x>=1 är integralen snäll och begränsad.