Konvergent eller divergent
Hur behandlar man dem här 😭
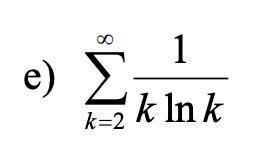
Måste jag behandla var för sig?
Vi har ju att välja på de gamla vanliga testerna. Rottestet, kvottestet, jämförelsetestet, o.s.v.
Jag som gillar integraler tycker att det är alldeles för sällan man drar fram integraltestet. Vad sägs om att vi prövar integraltestet här?
AlvinB skrev:Vi har ju att välja på de gamla vanliga testerna. Rottestet, kvottestet, jämförelsetestet, o.s.v.
Jag som gillar integraler tycker att det är alldeles för sällan man drar fram integraltestet. Vad sägs om att vi prövar integraltestet här?
Jag känner inte till rottestet och kvottestet.
Skulle det funka att säga att min serien är mindre än och därför konvergerar?
dajamanté skrev:AlvinB skrev:Vi har ju att välja på de gamla vanliga testerna. Rottestet, kvottestet, jämförelsetestet, o.s.v.
Jag som gillar integraler tycker att det är alldeles för sällan man drar fram integraltestet. Vad sägs om att vi prövar integraltestet här?
Jag känner inte till rottestet och kvottestet.
Skulle det funka att säga att min serien är mindre än och därför konvergerar?
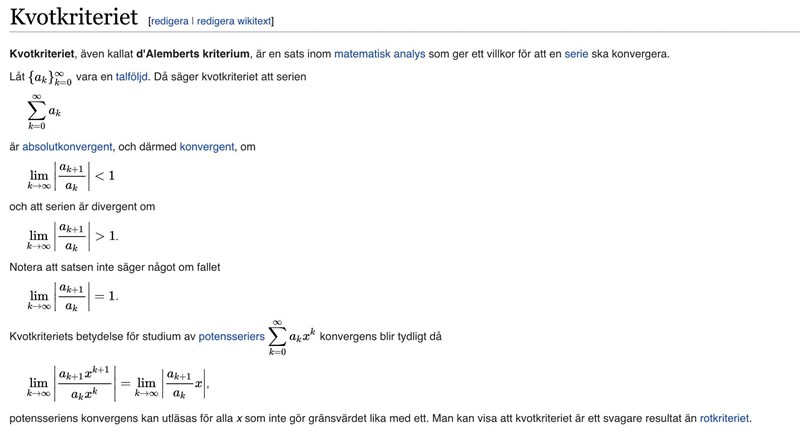
Kvottestet borde du ha hört talas om. Det är typ det första testet man lär sig. Du kanske har hört namnet d'Alemberts kriterium. Men struntsamma, varken kvottestet eller rottestet fungerar för denna serie.
Tyvärr är det så att integralen du nämner är mindre än serien. Det går således inte att visa att serien konvergerar på detta sätt.
Jag vet inte om du har arbetat med integraltestet förut. Poängen med det är att man integrerar samma funktion som man tar en summa av. Du skall alltså jämföra med integralen:
(Denna integral är faktiskt inte så svår att beräkna, även om den ser elak ut)
Det fiffiga med integraltestet är att summan konvergerar om och endast om integralen konvergerar. Om integralen konvergerar konvergerar alltså summan, och om integralen divergerar divergerar även summan.
Det finns några krav för att få använda integraltestet. Funktionen skall nämligen vara
- Positiv och kontinuerlig på intervallet
- Avtagande på intervallet
Du anar säkert att dessa två kriterier uppfylls eftersom jag föreslog integraltestet, men du bör även kunna motivera varför dessa två kriterier uppfylls.
WHAT??
WHAT??
Det har jag aldrig sett förut.
Det är som en magisk l'Hopital regel för serier!
Hur gör man i praktiken? Har du en bra uppgift?
(tack, jag klarade uppgiften med integral testet).
Ja, kvottestet ser rätt så fantastiskt ut, att man kan bestämma konvergens eller divergens endast med hjälp av ett gränsvärde. Dessvärre är det så att rätt många serier (denna uppgift med , till exempel) har det där jobbiga fallet där gränsvärdet blir lika med ett, och då säger kvottestet varken bu eller bä. Det är därför jag har för mig att man brukar börja med lära sig kvottestet eftersom det är ganska enkelt att tillämpa men inte så jätteanvändbart.
Vad sägs om att vi studerar summan:
med hjälp av kvottestet.
Okej.
Då blir det:
Kan det stämma?
Nja, det är lite slarv. skall vara i täljaren, du har satt det i nämnaren.
Ah sorry!
Men tvärtom då, ?
Just det, och det betyder att serien...
att
och därmed konvergent.
Tack AlvinB, det var en mycket bra tips.
Om vi ändå håller på att utforska olika sätt att bevisa konvergens kan vi också nämna Leibniz kriterium. Det råkar nämligen också gå att använda på mitt exempel. Leibniz kriterium säger att om:
- växlar tecken (d.v.s. varannan term är positiv, varannan är negativ)
- är minskande på intervallet
Så konvergerar summan
Att vår summa växlar tecken är ganska uppenbart (det går att bryta ut ). Att den är minskande kan visas med framåtdifferensoperatorn ("derivatan" för en diskret funktion, det låter krångligt, men är enligt mig enklare än vanlig derivata). Att gränsvärdet är lika med noll följer av att växer snabbare än . Alltså är summan konvergent.
Om du har tråkigt kan du även roa dig med att ta fram ett exakt värde på den här summan. Det går nämligen att visa att:
(Ett tips är att använda sig av en Taylorserie för den naturliga logaritmen)
Jag lovar att jag inte har det tråkigt just nu :D! Förberedder tentan fullt upp och jag är rädd att blanda ihop alla satser :).
Men jag läger en liten tjärna för utforskning lite senare!
AlvinB skrev:Om du har tråkigt kan du även roa dig med att ta fram ett exakt värde på den här summan. Det går nämligen att visa att:
(Ett tips är att använda sig av en Taylorserie för den naturliga logaritmen)
Uh nope...
Kom fram till
Jag tror inte att jag fattade vad du menade?
Du är på rätt spår. Du har ju Maclaurinserien:
om du skriver denna med sigmanotation får du:
Med lite jobb kan du få högerledet att se ut som:
Ser du hur?
Ja. Jag ser.

Nej, men allvarligt talat, jag förstår varför ln(8/11)!
Vad blir nu VL?

Jag Jag har n-1 i mitt eget formelblad, visst spelar det inga roll?
Jag kommer fram om några minuter ska skriva hur jag tänkte
AlvinB skrev:Vad blir nu VL?
Okej, nej. Jag tänkte alldeles fel.
Jag hade inte funderat ordentligt kring detta -1 helt enkelt. Sorry.
VL blir då ln(8/11).



