Koordinater

Antagligen har koordinatsystemet tre dimensioner. Observera skillnaden mellan ett tredimensionellt och ett tvådimensionellt koordinatsystem:

Tvådimensionellt:

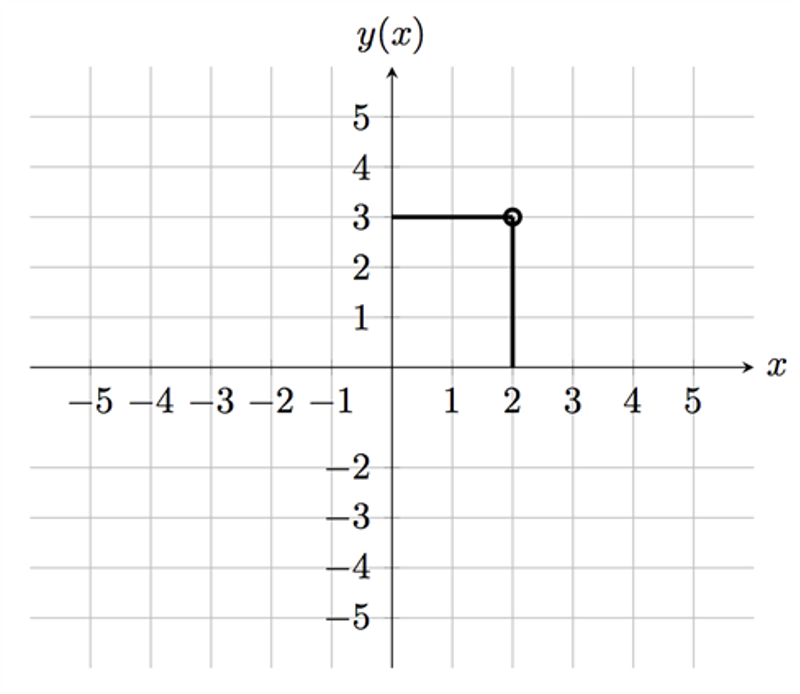
Tredimensionellt:

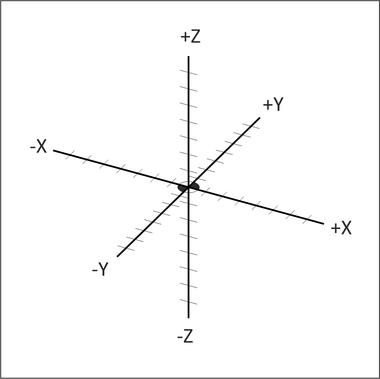
Låt A : (1,−2,3), B : (2,−1,0), C : (3,1,1) och D : (2,0,4).
(a) Visa att A, B, C och D utgör hörnen i en rektangel.
(b) Bestäm arean av rektangeln i (a)

Hur börjar jag med dessa?

Jag rekommenderar att du tittar på punkterna i ett koordinatsystem. Det skulle se ut ungefär så här:

Jag är lite osäker på hur man skulle visa att det verkligen är en rektangel, men arean kan du få fram genom att lösa för sidorna med hjälp av distansformeln (som även fungerar i tre dimensioner).

Kryssprodukten ger dig storleken på vinklarna. Om det är en rektangel är alla vinklarna $\pi /2$.

Borde man inte också behöva visa att punkterna ligger i ett plan? Skulle det vara nog med att med hjälp av distansformeln visa att de parallella sidorna är lika långa?

Även om de fyra punkterna ligger i ett plan och är parvis lika långa så är det ändå inte säkert att det är en rektangel.

Är medveten om det, men är det, i kombination med att visa att vinklarna är $90°$, nog för att säkert säga att det är en rektangel?

Bilda vektorer med hjälp av punkterna. Om de är parvis parallella samt att skalärprodukten mellan de icke-parallella vektorerna är noll måste det väl vara en rektangel.