Kraft och rörelse
Stämmer detta uppg a?

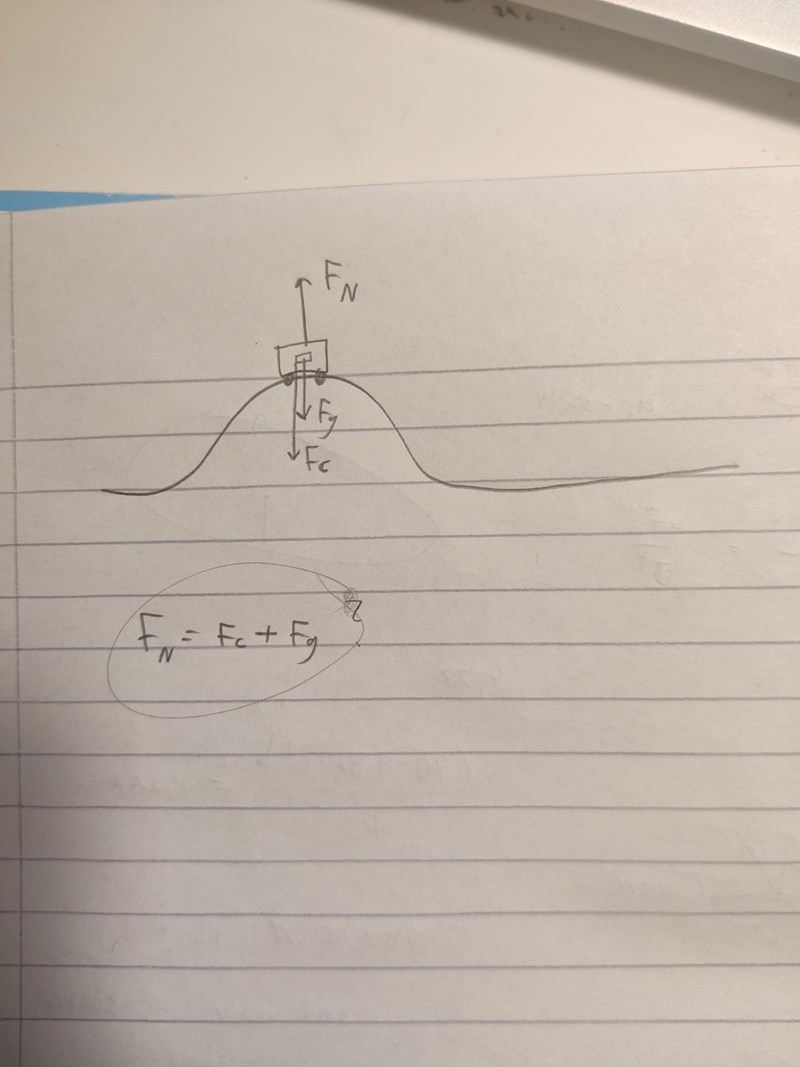
Det stämmer.
mrpotatohead skrev:Det stämmer.
FN borde då vara 29.6 N. Men facit säger 20N. Dessutom säger de att Fg är större än FN
Oj, tänkte nog fel.
Testa:
Fg = FN+Fc
Vad är Fc för något?
Anonym2005 skrev:
FN borde då vara 29.6 N. Men facit säger 20N. Dessutom säger de att Fg är större än FN
Din ursprungsbild stömmer inte riktigt.
Det är bara två krafter som verkar på lådan: Tyngdkraften Fg som verkar lodrätt neråt och normalkraften FN som verkar vinkelrätt mot sätet, se bild. (Jag har ritat sätet i blått för att tydliggöra var normalkraften angriper.)
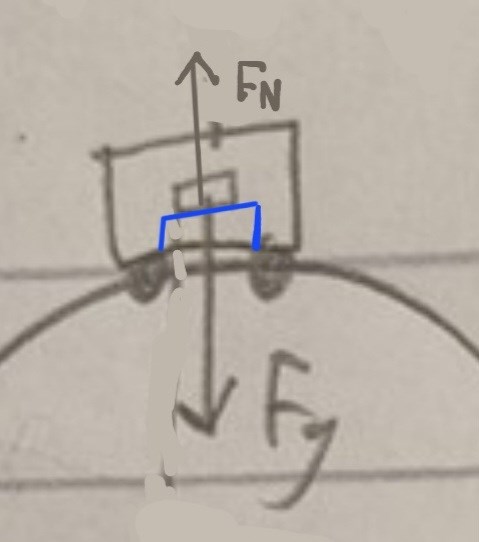
När bilen kör på plan mark så är FN och Fg lika stora och motriktade.
När bilen kör över krönet så accelererar bilen (och paketet) neråt och då minskar FN så att Fg > FN.
Om accelerationen neråt är tillräckligt stor (dvs om farten över backkrönet är tillräckligt stor eller om backkrönets radie är tillräckligt liten) så kommer FN att bli lika med 0. Då kommer både bilen och paketet att "lätta" från vägbanan.
Yngve skrev:Anonym2005 skrev:FN borde då vara 29.6 N. Men facit säger 20N. Dessutom säger de att Fg är större än FN
Din ursprungsbild stömmer inte riktigt.
Det är bara två krafter som verkar på lådan: Tyngdkraften Fg som verkar lodrätt neråt och normalkraften FN som verkar vinkelrätt mot sätet, se bild. (Jag har ritat sätet i blått för att tydliggöra var normalkraften angriper.)
När bilen kör på plan mark så är FN och Fg lika stora och motriktade.
När bilen kör över krönet så accelererar bilen (och paketet) neråt och då minskar FN så att Fg > FN.
Om accelerationen neråt är tillräckligt stor (dvs om farten över backkrönet är tillräckligt stor eller om backkrönets radie är tillräckligt liten) så kommer FN att bli lika med 0. Då kommer både bilen och paketet att "lätta" från vägbanan.
Blir Fg>Fn när centripetalkraften verkar? Jag förstår inte heller hur accelerationen neråt kan göra att paketet "lättar" från vägbanan?
Yngve skrev:Anonym2005 skrev:FN borde då vara 29.6 N. Men facit säger 20N. Dessutom säger de att Fg är större än FN
Din ursprungsbild stömmer inte riktigt.
Det är bara två krafter som verkar på lådan: Tyngdkraften Fg som verkar lodrätt neråt och normalkraften FN som verkar vinkelrätt mot sätet, se bild. (Jag har ritat sätet i blått för att tydliggöra var normalkraften angriper.)
När bilen kör på plan mark så är FN och Fg lika stora och motriktade.
När bilen kör över krönet så accelererar bilen (och paketet) neråt och då minskar FN så att Fg > FN.
Om accelerationen neråt är tillräckligt stor (dvs om farten över backkrönet är tillräckligt stor eller om backkrönets radie är tillräckligt liten) så kommer FN att bli lika med 0. Då kommer både bilen och paketet att "lätta" från vägbanan.
Om Fg är större än Fn, borde inte då bilen eller paketet åka ner? Under marken alltså?
Anonym2005 skrev:Om Fg är större än Fn, borde inte då bilen eller paketet åka ner? Under marken alltså?
De åker ner, i nedförsbacken.
Bubo skrev:Anonym2005 skrev:Om Fg är större än Fn, borde inte då bilen eller paketet åka ner? Under marken alltså?De åker ner, i nedförsbacken.
Men uppförsbacken borde det också gälla? Med konstant hastighet
Anonym2005 skrev:.
Men uppförsbacken borde det också gälla? Med konstant hastighet
Både hastigheten och accelerationen är vektorer, dvs storheter med både belopp och riktning.
Accelerationen är lika med förändringen av hastigheten per tidsenhet: .
Denna förändring kan dels bestå av att hastighetens belopp ändras (t.ex. när en bil på en rak plan väg ökar eller minskar farten), dels av att hastighetens riktning ändras (som t.ex. i detta fallet med backkrönet).
Accelerationen är här riktad mot en tänkt medelpunkt för den cirkel som backkrönet är en del av, dvs neråt (eller snett neråt innan/efter äversta punkten)
Yngve skrev:Anonym2005 skrev:.Men uppförsbacken borde det också gälla? Med konstant hastighet
Både hastigheten och accelerationen är vektorer, dvs storheter med både belopp och riktning.
Accelerationen är lika med förändringen av hastigheten per tidsenhet: .
Denna förändring kan dels bestå av att hastighetens belopp ändras (t.ex. när en bil på en rak plan väg ökar eller minskar farten), dels av att hastighetens riktning ändras (som t.ex. i detta fallet med backkrönet).
Accelerationen är här riktad mot en tänkt medelpunkt för den cirkel som backkrönet är en del av, dvs neråt (eller snett neråt innan/efter äversta punkten)
Ja, men jag tänker att eftersom bilen åker över backen, och inte dras under marken av en kraft, borde normalkraft när de åker vara lika med Fg och Fc, eftersom bilen inte åker ner i marken. Alltså tänker jag att Fc+Fg=Fn. Men hur är det inte så?
Yngve skrev:Anonym2005 skrev:.Men uppförsbacken borde det också gälla? Med konstant hastighet
Både hastigheten och accelerationen är vektorer, dvs storheter med både belopp och riktning.
Accelerationen är lika med förändringen av hastigheten per tidsenhet: .
Denna förändring kan dels bestå av att hastighetens belopp ändras (t.ex. när en bil på en rak plan väg ökar eller minskar farten), dels av att hastighetens riktning ändras (som t.ex. i detta fallet med backkrönet).
Accelerationen är här riktad mot en tänkt medelpunkt för den cirkel som backkrönet är en del av, dvs neråt (eller snett neråt innan/efter äversta punkten)
Nu syftar jag på fråga b, kanske inte självklart... Jag förstår att det bara är 2 krafter efter backen som verkar, så uppgift a har jag förstått. I uppgift a finns ingen centripetalkraft.
Anonym2005 skrev:Yngve skrev:Anonym2005 skrev:.Men uppförsbacken borde det också gälla? Med konstant hastighet
Både hastigheten och accelerationen är vektorer, dvs storheter med både belopp och riktning.
Accelerationen är lika med förändringen av hastigheten per tidsenhet: .
Denna förändring kan dels bestå av att hastighetens belopp ändras (t.ex. när en bil på en rak plan väg ökar eller minskar farten), dels av att hastighetens riktning ändras (som t.ex. i detta fallet med backkrönet).
Accelerationen är här riktad mot en tänkt medelpunkt för den cirkel som backkrönet är en del av, dvs neråt (eller snett neråt innan/efter äversta punkten)
Nu syftar jag på fråga b, kanske inte självklart... Jag förstår att det bara är 2 krafter efter backen som verkar, så uppgift a har jag förstått. I uppgift a finns ingen centripetalkraft.
Jo, visst finns det en centripetalkraft - backen är ju krökt!
Smaragdalena skrev:Anonym2005 skrev:Yngve skrev:Anonym2005 skrev:.Men uppförsbacken borde det också gälla? Med konstant hastighet
Både hastigheten och accelerationen är vektorer, dvs storheter med både belopp och riktning.
Accelerationen är lika med förändringen av hastigheten per tidsenhet: .
Denna förändring kan dels bestå av att hastighetens belopp ändras (t.ex. när en bil på en rak plan väg ökar eller minskar farten), dels av att hastighetens riktning ändras (som t.ex. i detta fallet med backkrönet).
Accelerationen är här riktad mot en tänkt medelpunkt för den cirkel som backkrönet är en del av, dvs neråt (eller snett neråt innan/efter äversta punkten)
Nu syftar jag på fråga b, kanske inte självklart... Jag förstår att det bara är 2 krafter efter backen som verkar, så uppgift a har jag förstått. I uppgift a finns ingen centripetalkraft.
Jo, visst finns det en centripetalkraft - backen är ju krökt!
Men uppgift a frågar väl om krafterna efter backen? Då finns ingen centripetalkraft?
Anonym2005 skrev:
Ja, men jag tänker att eftersom bilen åker över backen, och inte dras under marken av en kraft, borde normalkraft när de åker vara lika med Fg och Fc, eftersom bilen inte åker ner i marken. Alltså tänker jag att Fc+Fg=Fn. Men hur är det inte så?
Bilen åker "neråt". Men eftersom vägbanan har en krökning och bilen rör sig framåt så följer den bilens "neråtåkande".
Den situation du tänker på (att det måste gälla att Fg = FN) är relevant då bilen inte accelererar., dvs då den antingen står stilla eller då både hastighetens belopp och riktning är konstant.
Så är det inte i det här fallet eftersom bilen accelererar "neråt".
Anonym2005 skrev:
Men uppgift a frågar väl om krafterna efter backen? Då finns ingen centripetalkraft?
Nej, I uppgift a frågar de efter krafterna som påverkar bilen då den kör över backkrönet.
Du kan läsa om centripetalkraft i den här artikeln
Yngve skrev:Anonym2005 skrev:Ja, men jag tänker att eftersom bilen åker över backen, och inte dras under marken av en kraft, borde normalkraft när de åker vara lika med Fg och Fc, eftersom bilen inte åker ner i marken. Alltså tänker jag att Fc+Fg=Fn. Men hur är det inte så?
Bilen åker "neråt". Men eftersom vägbanan har en krökning och bilen rör sig framåt så följer den bilens "neråtåkande".
Den situation du tänker på (att det måste gälla att Fg = FN) är relevant då bilen inte accelererar., dvs då den antingen står stilla eller då både hastighetens belopp och riktning är konstant.
Så är det inte i det här fallet eftersom bilen accelererar "neråt".
Jag har kollat på 3 youtube videos och läst boken, men jag förstår verkligen inte.. Jag kan räkna på det (räkna ut centripetalkraften och göra svårare uppgifter) men det är bara riktningen som förvirrar mig. Kan jag istället ha det som minnesregel? Fn-mg=Fc?
I a-uppgiften skall man rita de lodräta krafter som verkar på paketet när bilen passerar krönet, d v s när bilen är på toppen av backen.





