Kraft och Rörelse

 Du får börja med att rita ut de krafter som verkar på vagnen. Då ser du att i rörelseriktningen har du en komposant av mg framåt och en friktionskraft bakåt. Summan (dvs. skillnaden i detta fall) av dessa ger massa * acceleration.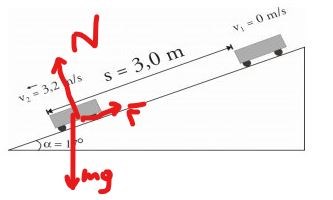

Så du menar att jag ska ta Kraftkomposanty-Kraftkomposantx = mxa? För kraftkomposant x är ju friktionskraften men kraftkomposant y är väl tyngdkraften?

Nvm, jag tror jag fattar! så det blir att räkna ut mg och sen använda trigonometri för att få fram resterande krafter?

Det sistnämnda är riktigt. Du ska alltså använda komposanten mg sin $\alpha$, tillsammans med hela friktionskraften F.

Så svaret blir alltså sin(17)xmg = 4,3N ? För xkomposanten är ju friktionskraften och det är ju det som dom frågar efter?

Friktionskraften är inte samma som x-komposanten av mg. Du får ställa upp ekvationen enligt accelerationslagen, integrera två gånger för att få sträckan som funktion av tiden, sätta in de givna siffrorna och på så sätt få fram F.

Accelerationslagen i riktning neråt längs planet (som du har angett som x-riktning): mg sin $\alpha$ - F = ma,

Vinkelrätt mot planet: N - mg cos $\alpha$ = 0 (det finns ingen acceleration i den riktningen). Du behöver inte denna ekvation i uppgiften.

Från den första ekvationen kan du bestämma accelerationen a, som: a = g sin $\alpha$ - F/m,

Integrera det en gång för att få hastigheten - här är accelerationen konstant så du kan använda v = at + $v_0$. Eftersom starten sker från vila är $v_0$ = 0.

Integrera en gång till så du får sträckan s = a$\frac{t^2}{2}$ + $s_0$. Du mäter sträckan från startläget, så $s_0$ = 0.

Sätter du nu in alla givna siffror får du fram F.

Okej tack!

Dock så har jag ju varken a eller F i början. Och via ekvationen du skrev "a = g sin α - F/m "så behöver jag ju ha F? eller menar du att F är mg?

F är inte mg. Du får accelerationen a genom villkoret på sträcka och tid. Har du a får du F ur det första sambandet.

Så alltså; ekvationen är F-mg sin(17) = mxa 

v=s/t -> t=s/v = 0,94s 

v=v0 + at -> a= (v-v0)/t -> 3,4m/s^2 

F= mxa + mg sin(17)  = 1,5 x 3,4 + (1.5 x 9,82 x sin(17)) = 9,2 N ?

Hastigheten är inte konstant, så du kan inte använda formeln v = s/t. Utgå från att accelerationen är konstant (eftersom alla krafter är konstanta). 

Men går det inte om jag räknar ut medelhastigheten först? så (v0+v1)/2  = 1.6m/s och sen tiden via t=s/v = 3/1.6 = 1.875s 

Och sen (v1-v0)/t =  a= 1.7m/s^2 

Ffr - F =mxa -> F= Ffr- mxa =  ( mgsin(17)) - 1.7x1.5 = 1.7N

Jo, med medelhastigheten blir det riktigt. Sträckan = medelhastigheten * tiden. Men du måste vara klar över förutsättningarna, att medelhastigheten kan beräknas som (v0+v1)/2 bara om hastigheten ändras linjärt (som a*t).