Kraft på ledare i magnetfält

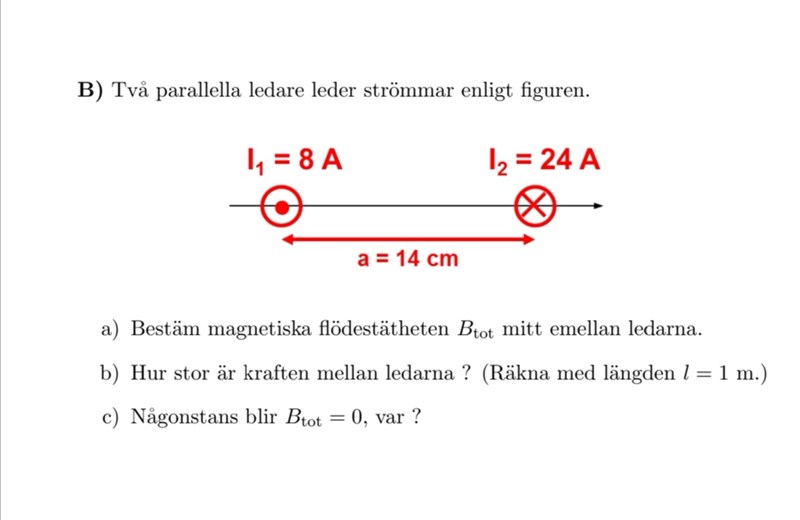
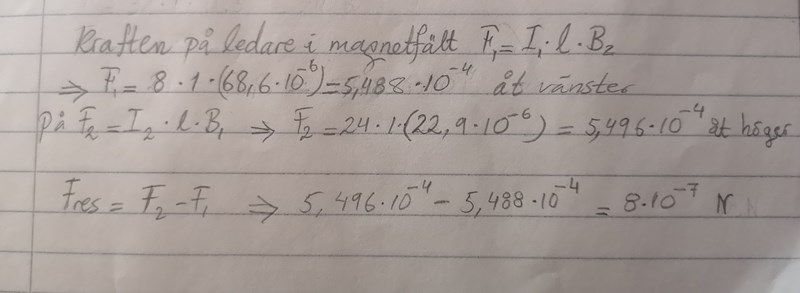
Det framgår inte hur du har räknat ut B2. 

$F_1 = B_2I_1L_1$

där 

$B_2= k\dfrac{I_2}{a}$

Det är F1 du vill räkna ut, inte F1 - F2 (som blir 0, varför?).

Dr. G skrev:

Det framgår inte hur du har räknat ut B2. 

$F_1 = B_2I_1L_1$

där 

$B_2= k\dfrac{I_2}{a}$

Det är F1 du vill räkna ut, inte F1 - F2 (som blir 0, varför?).

Jag ville beräkna kraften mellan ledarna, och det är två krafter som verkar.. Varför bara F1? 

De frågar efter kraften från magnetfältet från ledare 2 på ledare 1 (eller tvärtom). 

(Mittemellan ledarna finns ingen ström, så ingen magnetisk kraft.)

Dr. G skrev:

De frågar efter kraften från magnetfältet från ledare 2 på ledare 1 (eller tvärtom). 

(Mittemellan ledarna finns ingen ström, så ingen magnetisk kraft.)

Jahaa.. Jag fattar nu, tackkk för hjälp 😊😊😊

Behöver också hjälp i c) uppgift samma fråga. 

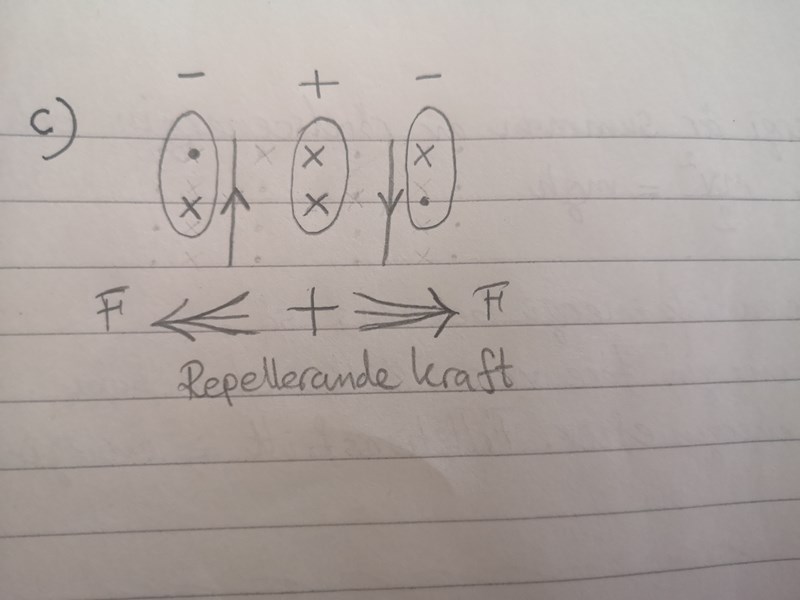
Jag ritade figur på flödestätheten runt ledarna.. Fattar inte riktigt vart ska Btot ska finnas? 

Hur ser det totala fältet ut till höger och till vänster om de båda ledarna?

Alltså till vänster om $I_1$ och till höger om $I_2$

Jroth skrev:

Hur ser det totala fältet ut till höger och till vänster om de båda ledarna?

Alltså till vänster om $I_1$ och till höger om $I_2$

Jo det blir närmare noll på båda.. Så de bör ta ut varandra på både höger sida om I2 och vänster sida om I1.. Men varför står det i facit att de tar ut varandra bara på vänster sidan om I1 och exakr 7cm från den? 

På vänster och på höger sida avtar fälten. Men de är också motriktade och tar vill viss del ut varandra.

På den högra sidan kommer fältet från ledaren med den högre strömstyrkan alltid vara starkare än (vinna över) fältet från ledaren med den lägre strömstyrkan.

På den vänstra sidan kan fältet från den vänstra ledaren ta ut fältet från den högra ledaren, det beror på att den svagare strömstyrkan kompenseras av ett kortare avstånd.

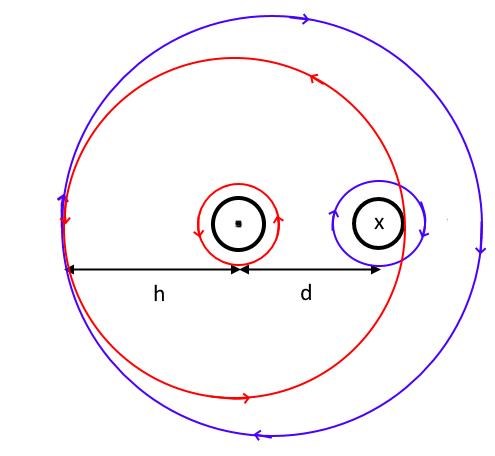
B-fälten tar ut varandra när de är lika stora, fast motriktade

$B_1=B_2$

$\frac{\mu_0I_1}{2\pi h}=\frac{\mu_0I_2}{2\pi (h+d)}$

$B_1=B_2$

$\frac{\mu_0I_1}{2\pi h}=\frac{\mu_0I_2}{2\pi (h+d)}$

Ahaa fint, förstår förklaringen👍🏻.. Men den sista formel var nytt för mig eftersom den finns inte i boken.. Bara B=k*I/a

En fråga😁, varför är inte ledare 2 placerad mitt i dess flödestätheten som det är för ledare 1? 

jag löste det, hoppas att det ser bra ut.. Tack för hjälp

På din första fråga, min bild är dålig eftersom jag är lite slarvig när jag målar. Båda fälten ska vara centrerade.

På din andra fråga: Använd att fälten ska vara lika stora men motriktade när de tar ut varandra. Det ger en ekvation som du ska lösa.

Med din formel för den vänstra sidan:

$B1=B2$

$\frac{kI_1}{h}=\frac{kI_2}{h+d}$

Multiplicera båda led med (h+d)

$\frac{(kI_1)(h+d)}{h}=kI_2$

Multiplicera båda led med h

$kI_1(h+d)=kI_2h$

Multiplicera in och isolera h

$kh(I_2-I_1)=kI_1d$

$h=\frac{I_1d}{I_2-I_1}=7\mathrm{cm}$

Jroth skrev: ... 

Aha, fint.. Det ska jag addera i min beräkning för att visa hur jag kom fram till att avståndet blir 7cm eller kanske ritar jag det som du gjort..Tack ska du ha🌸