Krafter
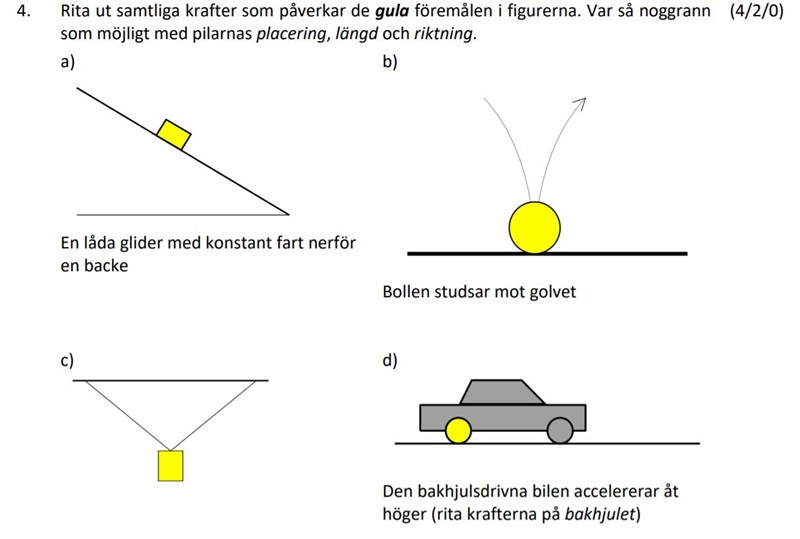
Uppgiften går ut på att rita ut krafterna på de gula föremålen
Svar: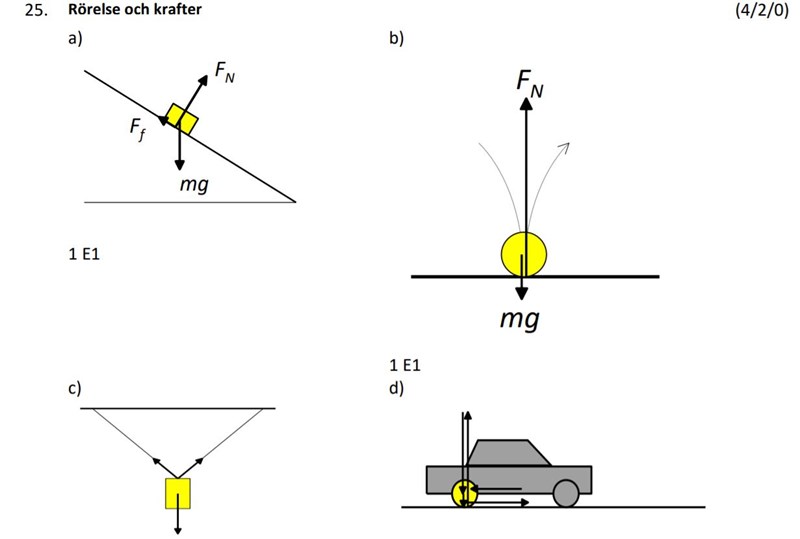
På a) där, borde inte gravitationskraften vara lika stor som normalkraften och friktionskraften tillsamman? På bilden ser det ut som att normalkraften är lika stor som gravitationskraften.
Sedan på d), det ser ju väldigt stökigt ut tycker jag. Ska inte gravitationskraften finnas med där också?
Först a-uppgiften: Den pil du ser som beskriver gravitationskraft går ju från mitten av lådan (man tänker väl tyngdpunkt antar jag), medan normalkraften går från mitten av ytan mellan planet (backen) och lådan. Det är sant som du säger att normalkraft och gravitationskraft och friktionskraft tillsammans ska bli noll, men det är inte längderna av pilarna man lägger ihop, utan man ska lägga ihop dom som "vektoraddition".
Det finns en intressant slamkrypare här som du nästan har upptäckt. Friktionskraften är normalt proportionell mot normalkraften med en proportionalitetskonstant som kallas friktionskoefficient (betecknas ofta med grekiska - "my") -- för att lådan ska kunna få någon fart, och om vi antar att det är en låda som av något skäl börjar glida nerför en backe -- inte att något givit den fart genom att sätta den i rörelse med en utgångshastighet, så måste den antingen ha en acceleration, vilken den får om kraftpilarna tillsammans inte är noll, dvs den är inte i jämvikt. Den resulterande kraften som uppstår om man lägger ihop alla krafter och får något som inte är noll ger lådan en acceleration som är F/m. F är den resulterande kraften och m är lådans massa. I praktiken, om man sätter sig i en låda och åker nerför en backe, så kommer en annan kraft -- luftmotståndet, som är beroende på hastigheten på ett inte så enkelt sätt, att öka till dess att friktionskraften (som finns i ditt facit) och luftmotståndet (som saknas där) blir lika stora som resulterande kraften från normalkraft och tyngdkraft. På det viset tycker jag att svaret i dit fall saknar luftmotståndet.
Vad gäller d-uppgiften tycker jag som du att det är lite rörigt. Jag tror att den långa pilen längs till vänster uttrycker gravitationskraften från bilens vikt på hjulet (som kommer genom hjulaxeln); den kortare, också den nedåtriktade pilen från hjulets centrum är hjulets egen tyngd. Den övre pilen till höger som är riktad bakåt är tröghetskraften från bilen som bilens acceleration ger upphov till - den är också placerad i bilens mitt, antagligen tänkt som masscentrum. Den undre pilen är friktionskraften från asfalten (underlaget) som drar bilen framåt. Till skillnad från tyngdaccelerationens pilar (de två vänstra pilarna) som tar med bidraget från både bil och hjulet självt så tycker jag att det saknas en kraft för hjulets (förutom resten av bilen) acceleration. Jag gissar att problemförfattaren har tänkt att den är inräknad i den övre pilen till höger, men du har rätt -- en pil från hjulets centrum bakåt som uttrycker hjulets tröghet vid acceleration borde finnas med.
PeBo skrev:Först a-uppgiften: Den pil du ser som beskriver gravitationskraft går ju från mitten av lådan (man tänker väl tyngdpunkt antar jag), medan normalkraften går från mitten av ytan mellan planet (backen) och lådan. Det är sant som du säger att normalkraft och gravitationskraft och friktionskraft tillsammans ska bli noll, men det är inte längderna av pilarna man lägger ihop, utan man ska lägga ihop dom som "vektoraddition".
Det finns en intressant slamkrypare här som du nästan har upptäckt. Friktionskraften är normalt proportionell mot normalkraften med en proportionalitetskonstant som kallas friktionskoefficient (betecknas ofta med grekiska - "my") -- för att lådan ska kunna få någon fart, och om vi antar att det är en låda som av något skäl börjar glida nerför en backe -- inte att något givit den fart genom att sätta den i rörelse med en utgångshastighet, så måste den antingen ha en acceleration, vilken den får om kraftpilarna tillsammans inte är noll, dvs den är inte i jämvikt. Den resulterande kraften som uppstår om man lägger ihop alla krafter och får något som inte är noll ger lådan en acceleration som är F/m. F är den resulterande kraften och m är lådans massa. I praktiken, om man sätter sig i en låda och åker nerför en backe, så kommer en annan kraft -- luftmotståndet, som är beroende på hastigheten på ett inte så enkelt sätt, att öka till dess att friktionskraften (som finns i ditt facit) och luftmotståndet (som saknas där) blir lika stora som resulterande kraften från normalkraft och tyngdkraft. På det viset tycker jag att svaret i dit fall saknar luftmotståndet.
Vad gäller d-uppgiften tycker jag som du att det är lite rörigt. Jag tror att den långa pilen längs till vänster uttrycker gravitationskraften från bilens vikt på hjulet (som kommer genom hjulaxeln); den kortare, också den nedåtriktade pilen från hjulets centrum är hjulets egen tyngd. Den övre pilen till höger som är riktad bakåt är tröghetskraften från bilen som bilens acceleration ger upphov till - den är också placerad i bilens mitt, antagligen tänkt som masscentrum. Den undre pilen är friktionskraften från asfalten (underlaget) som drar bilen framåt. Till skillnad från tyngdaccelerationens pilar (de två vänstra pilarna) som tar med bidraget från både bil och hjulet självt så tycker jag att det saknas en kraft för hjulets (förutom resten av bilen) acceleration. Jag gissar att problemförfattaren har tänkt att den är inräknad i den övre pilen till höger, men du har rätt -- en pil från hjulets centrum bakåt som uttrycker hjulets tröghet vid acceleration borde finnas med.
Använde faktiskt vektor addition på a) och mätte med linjal. Fg blev fortfarande mindre. Jag antar att det är bara lite med uppgiften. Tack så mycket

