Kraftmoment med sne vinkel
Hej, har lite problem med att räkna ut spänningen på repet. Massan bidrar med på repet och även massan måste bidra, men hur mycket? ligger ju inte direkt vid punkten utan på ett avståndet av . Hur gör jag då? var inne på att hitta kraftkomposanten till parallell till repet men beräkningar blir riktigt grötiga (samt avståndet spökar) vilket får mig att bli misstänksam att jag är ute och cyklar.
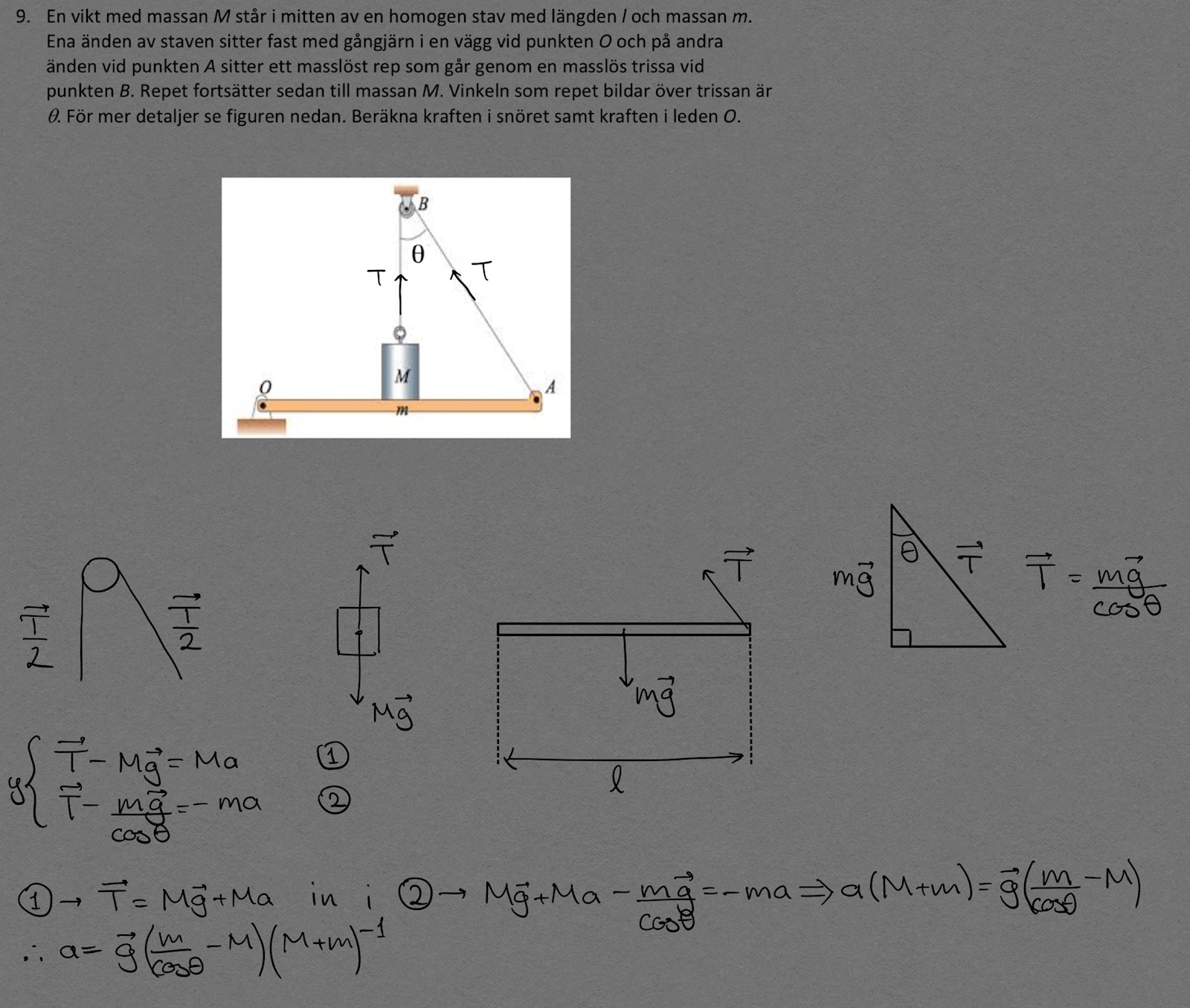
Cien skrev:Massan bidrar med på repet
Det kan du inte anta.
Du missar vissa krafter i din friläggning.
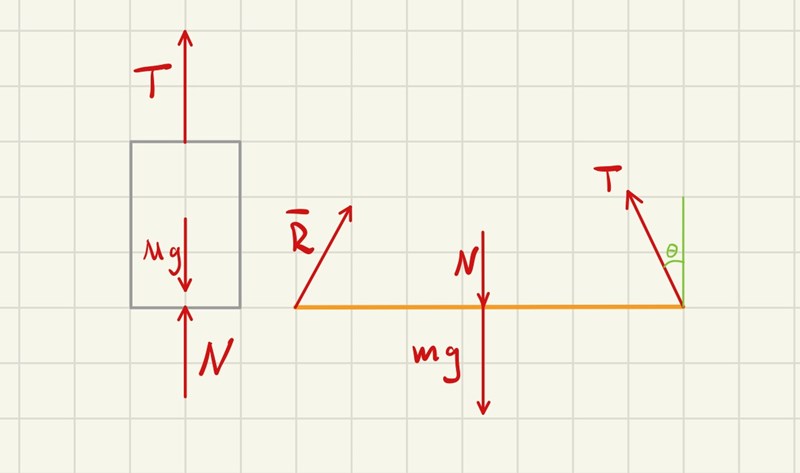
PATENTERAMERA skrev:Du missar vissa krafter i din friläggning.
Tackar. Vad är R för kraft?
Den sökta kraften vid leden O. Du kan låta den bestå av komposanterna
PATENTERAMERA skrev:Du missar vissa krafter i din friläggning.
Hur går tänket när du ritar upp krafterna till M? jag tänker att M knappt är i kontakt med staven (hänger i repet) och därmed ingen normalkraft
Edit: Och hur kommer det sig att normalkraften är neråt och inte uppåt?
Cien skrev:PATENTERAMERA skrev:Du missar vissa krafter i din friläggning.
Hur går tänket när du ritar upp krafterna till M? jag tänker att M knappt är i kontakt med staven (hänger i repet) och därmed ingen normalkraft
Edit: Och hur kommer det sig att normalkraften är neråt och inte uppåt?
Patenterameras ritning visar mycket tydligt hur kraften uppåt från brädan på vikten är lika stor som viktens kraft på brädan. Men åt motsatt håll. Helt enligt Newton.
Pieter Kuiper skrev:Cien skrev:PATENTERAMERA skrev:Du missar vissa krafter i din friläggning.
Hur går tänket när du ritar upp krafterna till M? jag tänker att M knappt är i kontakt med staven (hänger i repet) och därmed ingen normalkraft
Edit: Och hur kommer det sig att normalkraften är neråt och inte uppåt?
Patenterameras ritning visar mycket tydligt hur kraften uppåt från brädan på vikten är lika stor som viktens kraft på brädan. Men åt motsatt håll. Helt enligt Newton.
I figur 1 är N uppåt och i figur 2 neråt, varför?
Som sagts, kraft och motkraft. Brädan påverkar vikten med en kraft uppåt och då påverkar vikten brädan med en lika stor men motriktad kraft.
PATENTERAMERA skrev:Som sagts, kraft och motkraft. Brädan påverkar vikten med en kraft uppåt och då påverkar vikten brädan med en lika stor men motriktad kraft.
N=Mg?
Nej, en del av viktens tyngd tas upp av spännkraften i repet. Det är tyvärr en vanlig missuppfattning att normalkraften är en reaktionskraft till tyngdkraften.
Normalkraften är (den vinkelräta) kontaktkraften mellan två kontaktytor och behöver inte ha med tyngdkraften att göra. Du får anta att den är okänd tills vidare och ställa upp jämvikt i x- och y-led för vikten och plankan.
D4NIEL skrev:Nej, en del av viktens tyngd tas upp av spännkraften i repet. Det är tyvärr en vanlig missuppfattning att normalkraften är en reaktionskraft till tyngdkraften.
Normalkraften är (den vinkelräta) kontaktkraften mellan två kontaktytor och behöver inte ha med tyngdkraften att göra. Du får anta att den är okänd tills vidare och ställa upp jämvikt i x- och y-led för vikten och plankan.
Ok tror jag är med nu, rätta mig gärna om jag har fel men vi förutsätter att M till viss del är i kontakt med brädan (ger upphov till kontaktkraft N) samt att M till viss del hänger i repet (ger upphov till spänningskraft T)?
Ja, M uppbärs dels av dels av . Din uppgift nu är alltså att bestämma och . Till din hjälp har du ett antal jämviktsvillkor:
Summan av samtliga krafters komposanter i en viss riktning ska vara noll.
Summan av samtliga krafters moment kring en viss axel ska vara noll.
D4NIEL skrev:Ja, M uppbärs dels av dels av . Din uppgift nu är alltså att bestämma och . Till din hjälp har du ett antal jämviktsvillkor:
Summan av samtliga krafters komposanter i en viss riktning ska vara noll.
Summan av samtliga krafters moment kring en viss axel ska vara noll.
Tack Daniel dina svar uppskattas alltid! Och alla andra svar med för den delen!
D4NIEL skrev:Ja, M uppbärs dels av dels av . Din uppgift nu är alltså att bestämma och . Till din hjälp har du ett antal jämviktsvillkor:
Summan av samtliga krafters komposanter i en viss riktning ska vara noll.
Summan av samtliga krafters moment kring en viss axel ska vara noll.
Jag tänkte hitta T's kraftkomposant i y-led, är då ?
Du glömmer reaktionskraften i O; den kan ha en y-komponent Ry som är skild från 0.
PATENTERAMERA skrev:Du glömmer reaktionskraften i O; den kan ha en y-komponent Ry som är skild från 0.
Jag har inte satt in dem i ekvationssystemet än, ville först ordna kraften i y-led i punkten A
Vad menar du med att ordna kraften i y-led i A?
PATENTERAMERA skrev:Vad menar du med att ordna kraften i y-led i A?
Att jag får kraften T y-leds komposant i punkten A
Men det är väl bara T?
PATENTERAMERA skrev:Men det är väl bara T?
Oj Sorry blandade ihop det med något helt annat, tack :)
D4NIEL skrev:Ja, M uppbärs dels av dels av . Din uppgift nu är alltså att bestämma och . Till din hjälp har du ett antal jämviktsvillkor:
Summan av samtliga krafters komposanter i en viss riktning ska vara noll.
Summan av samtliga krafters moment kring en viss axel ska vara noll.
Jag har lagt vridningsaxeln i O och får
<- från staven
<- från vikten M
Två ekvationer, 4 obekanta, saknar lösning.
Edit: Blir lite förvirrad, ska jag verkligen ha två ekvationssystem. Mitt tänk va, två friläggningar, två ekvationer. Kanske är fel?
Du kan sätta upp en ekvation för vikten. Jämvikt i y-led. T + N - Mg = 0.
Du kan sätta upp tre ekvationer för stången: jämvikt i x- och y-led samt momentekvation tex kring O.
Fyra obekanta. Fyra ekvationer.
PATENTERAMERA skrev:Du kan sätta upp en ekvation för vikten. Jämvikt i y-led. T + N - Mg = 0.
Du kan sätta upp tre ekvationer för stången: jämvikt i x- och y-led samt momentekvation tex kring O.
Fyra obekanta. Fyra ekvationer.
Förresten går det att använda mitt ekvationssystem i svaret innan? Eftersom i uppgiften står det att viktens massa är M och stavens massa m. Så då har ekvationssystem 2 obekanta
Den första ekvationen ser rätt ut. Men den andra förstår jag inte hur du kom fram till. Använd T + N - Mg = 0 i stället. Sedan måste du i alla fall ställa upp ytterligare ekvationer för att få ut Rx och Ry.
PATENTERAMERA skrev:Den första ekvationen ser rätt ut. Men den andra förstår jag inte hur du kom fram till. Använd T + N - Mg = 0 i stället. Sedan måste du i alla fall ställa upp ytterligare ekvationer för att få ut Rx och Ry.
Den andra ekvationen jag har skrivit är precis T+N-Mg=0, det är dock avstånden till vridningsaxeln som är med
Nja, om du delar med l så blir din ekvation T + N/2 - Mg/2 = 0, vilket inte riktigt är samma.
PATENTERAMERA skrev:Nja, om du delar med l så blir din ekvation T + N/2 - Mg/2 = 0, vilket inte riktigt är samma.
Varför är detta fel? Vi ställer ju upp kraftmomentets ekvationer
Nja, du har redan satt upp en momentekvation för stången - din första ekvation. För vikten kan du bara sätta upp kraftjämvikt i y-led.
PATENTERAMERA skrev:Nja, du har redan satt upp en momentekvation för stången - din första ekvation. För vikten kan du bara sätta upp kraftjämvikt i y-led.
Sitter här och tänker på kraften R, vet inte hur jag ska hitta kraftkomposanter i x- och y-led då jag inte har någon vinkel
Ansätt = (Rx, Ry). Dvs två obekanta komponenter Rx och Ry.
PATENTERAMERA skrev:Ansätt = (Rx, Ry). Dvs två obekanta komponenter Rx och Ry.
Okej och löser ut Rx och Ry med Pythagoras?
Nja, du kan sätta upp kraftjämvikt för stången.
Rx - Tsin = 0.
Ry - N - mg + Tcos = 0.
Räkna ut T och N från tidigare ekvationer och sätt in i ekvationerna ovan. Lös ut Rx och Ry.
PATENTERAMERA skrev:Nja, du kan sätta upp kraftjämvikt för stången.
Rx - Tsin = 0.
Ry - N - mg + Tcos = 0.
Räkna ut T och N från tidigare ekvationer och sätt in i ekvationerna ovan. Lös ut Rx och Ry.
Har kommit fram till detta, hoppas det är rätt. Hur ska jag nu lösa R
Edit: Antar att vi ska lösa R med hjälp av linjär algebra (som jag är kass på :P)
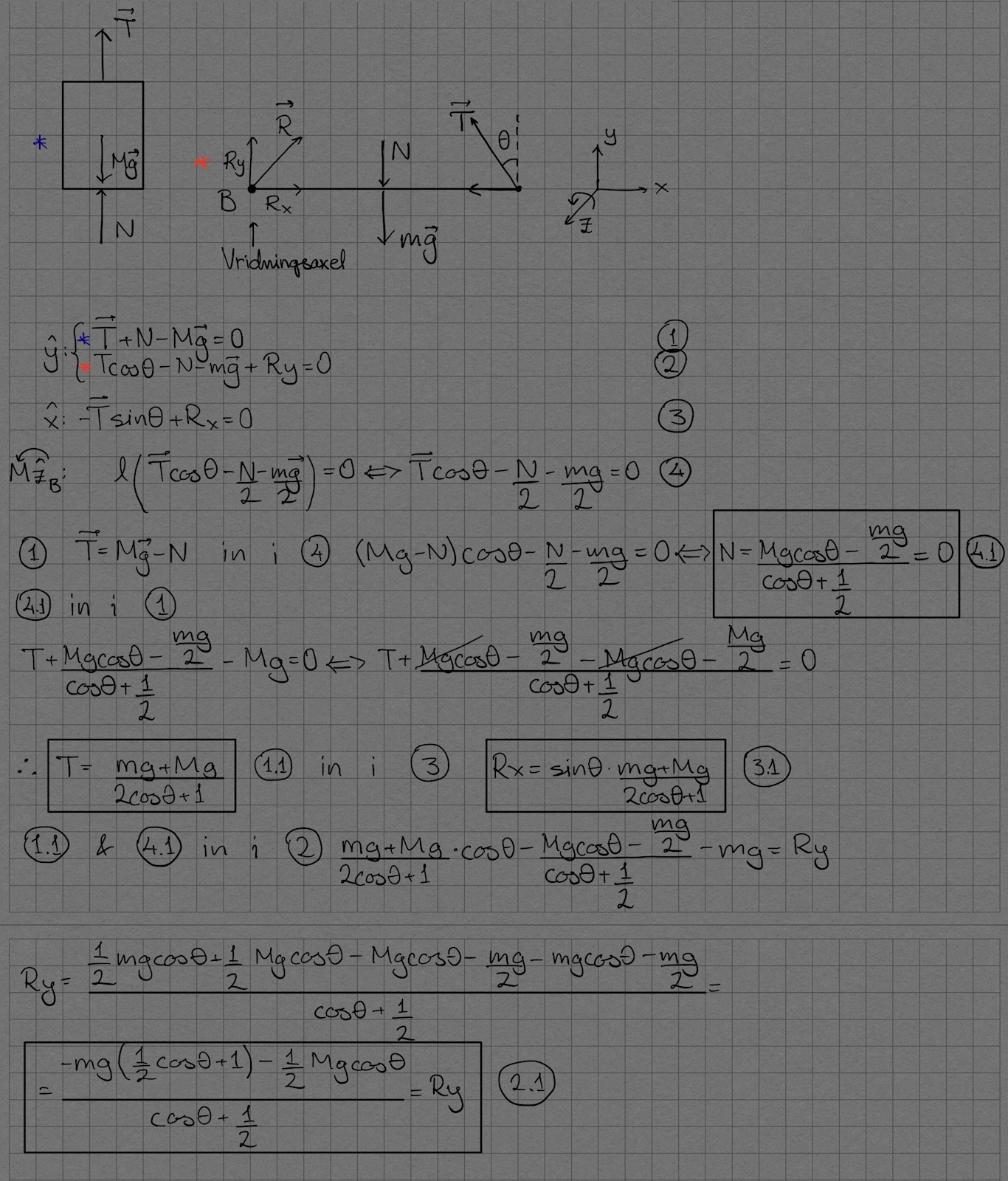
Testa om det stämmer med något värde av vinkeln, till exempel eller .
Du kan även välja värden för massorna.
Pieter Kuiper skrev:Testa om det stämmer med något värde av vinkeln, till exempel eller .
Du kan även välja värden för massorna.
Smart! Det ska jag göra
Pieter Kuiper skrev:Testa om det stämmer med något värde av vinkeln, till exempel eller .
Du kan även välja värden för massorna.
Grymt nu är leden i ES lika!
Edit: Nu hittar jag genom att helt enkelt ?

Cien skrev:Pieter Kuiper skrev:Testa om det stämmer med något värde av vinkeln, till exempel eller .
Du kan även välja värden för massorna.Grymt nu är leden i ES lika!
Edit: Nu hittar jag genom att helt enkelt ?
Så trevligt!
Ja, och använd att .
Pieter Kuiper skrev:Cien skrev:Pieter Kuiper skrev:Testa om det stämmer med något värde av vinkeln, till exempel eller .
Du kan även välja värden för massorna.Grymt nu är leden i ES lika!
Edit: Nu hittar jag genom att helt enkelt ?
Så trevligt!
Ja, och använd att .
Får , stämmer med värdena jag antog,
Har bara en fråga om friläggningen, hur tänker man när man ritade vektorpilen till R i friläggningen, varför peka den upp åt höger?
Allt gott
Och när .
Och nu var det inte jag som gjorde den fina ritningen, men gångjärnet ger stöd uppåt åt höger. Tänk vad skulle hända om gångjärnet inte fanns. Brädan skulle ramla ner. Eller glida till vänster om den låg på ett bord.
Pieter Kuiper skrev:Och när .
Och nu var det inte jag som gjorde den fina ritningen, men gångjärnet ger stöd uppåt åt höger. Tänk vad skulle hända om gångjärnet inte fanns. Brädan skulle ramla ner. Eller glida till vänster om den låg på ett bord.
Mycket logiskt, tack!


