Krånglig fouriertransform uppgift

Den givna funktionen $f$ är udda (d.v.s. symmetrisk i origo, d.v.s. $f(-x)=-f(x)$). När man skriver ut exp(-i omega x) enligt Eulers formel, så kan man utnyttja symmetrin i integralen som definierar fouriertransformen.

$\displaystyle \int_{-\infty}^\infty f\left(x\right)\,e^{-i\omega x}\,dx = \int_{-a}^a (f\left(x\right)\,\cos\left(\omega x\right)-i\,\sin\left(\omega x\right))\,dx$

$\displaystyle = \int_{-a}^a \underbrace{f\left(x\right)\,\cos\left(\omega x\right)}_{\text{udda, så integralen=0}}\,dx - i\,\int_{-a}^a \underbrace{f\left(x\right)\,\sin\left(\omega x\right)}_{\text{jämn}}\,dx = -2i\,\int_0^a 1\cdot \sin\left(\omega x\right) \,dx = \ldots$

När du beräknat denna integral och därmed tagit fram fouriertransformen till $f$, så får du nog skriva ut integralen i inversa fouriertransformen och utnyttja symmetrin på liknande sätt.

För tydlighetens skull får du kanske döpa om integrationsvariabeln i

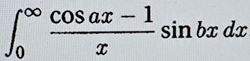
till $\omega$, d.v.s. skriv $\displaystyle \int_0^\infty \frac{\cos(a\omega)-1}{\omega}\,\sin\left(b\omega\right)\,d\omega$. Notera också att uttrycket $\dfrac{\cos(a\omega)-1}{\omega}$ är en udda funktion.

LuMa07 skrev:

Den givna funktionen $f$ är udda (d.v.s. symmetrisk i origo, d.v.s. $f(-x)=-f(x)$). När man skriver ut exp(-i omega x) enligt Eulers formel, så kan man utnyttja symmetrin i integralen som definierar fouriertransformen.

$\displaystyle \int_{-\infty}^\infty f\left(x\right)\,e^{-i\omega x}\,dx = \int_{-a}^a (f\left(x\right)\,\cos\left(\omega x\right)-i\,\sin\left(\omega x\right))\,dx$

$\displaystyle = \int_{-a}^a \underbrace{f\left(x\right)\,\cos\left(\omega x\right)}_{\text{udda, så integralen=0}}\,dx - i\,\int_{-a}^a \underbrace{f\left(x\right)\,\sin\left(\omega x\right)}_{\text{jämn}}\,dx = -2i\,\int_0^a 1\cdot \sin\left(\omega x\right) \,dx = \ldots$

När du beräknat denna integral och därmed tagit fram fouriertransformen till $f$, så får du nog skriva ut integralen i inversa fouriertransformen och utnyttja symmetrin på liknande sätt.

 

För tydlighetens skull får du kanske döpa om integrationsvariabeln i

till $\omega$, d.v.s. skriv $\displaystyle \int_0^\infty \frac{\cos(a\omega)-1}{\omega}\,\sin\left(b\omega\right)\,d\omega$. Notera också att uttrycket $\dfrac{\cos(a\omega)-1}{\omega}$ är en udda funktion.

Var ska jag börja?

Beräkna Fouriertransformen till $f$ och utnyttja symmetrin i integralen

LuMa07 skrev:

Beräkna Fouriertransformen till $f$ och utnyttja symmetrin i integralen

Vad menar du med symmetri? Ska jag beräkna fouriertransformen till f mha definitionen?

Beräkna fouriertransformen enligt definitionen och använd det faktum att f(x) är udda.

Därmed är f(x) cos(ωx) också udda, medan f(x) sin(ωx) är jämn.

LuMa07 skrev:

Beräkna fouriertransformen enligt definitionen och använd det faktum att f(x) är udda.

Därmed är f(x) cos(ωx) också udda, medan f(x) sin(ωx) är jämn.

Hur vet jag att f(x) är udda eller jämn? Är detta något man får reda på när man tagit fram fouriertransformen till f?

Jag har fastnat på hur man ska använda definitionen samt dela upp integralen med de givna gränserna. Jag har också svårt att inse varför funktionen är jämn eller udda och hur man vet det bara av att se på uppgiften.

En funktion är udda om f(-x) = f(x) och jämn om f(-x) = f(x).

I detta falla är det enkelt att se att f är udda från definitionen.

Integralen av en udda funktion mellan -a och a är noll.

Integralen av en jämn funktion mellan -a och a är 2 gånger integralen från 0 till a.

PATENTERAMERA skrev:

En funktion är udda om f(-x) = f(x) och jämn om f(-x) = f(x).

I detta falla är det enkelt att se att f är udda från definitionen.

Integralen av en udda funktion mellan -a och a är noll.

Integralen av en jämn funktion mellan -a och a är 2 gånger integralen från 0 till a.

Ja alltså jag håller med dig om allt gällande jämn och udda. Jag ser bara inte hur funktionen i frågan är jämn eller udda. 

destiny99 skrev:

Ja alltså jag håller med dig om allt gällande jämn och udda. Jag ser bara inte hur funktionen i frågan är jämn eller udda. 

Du kan testa de olika fallen på $x$:

Om $0 <x\leq a$ får vi att $f(x) = 1$ och då är $-a\leq-x <0$, vilket ger $f(-x) = -1 = -f(x)$. Sedan får man undersöka de andra möjliga fallen på $x$.

Kan också hjälpa med en bild på funktionen:


(Tekniskt sett är funktionen inte udda i $x=0$, men för integralerna kvittar det helt då det endast är en punkt)

AlexMu skrev:

destiny99 skrev:

Ja alltså jag håller med dig om allt gällande jämn och udda. Jag ser bara inte hur funktionen i frågan är jämn eller udda. 

Du kan testa de olika fallen på $x$:

Om $0 <x\leq a$ får vi att $f(x) = 1$ och då är $-a\leq-x <0$, vilket ger $f(-x) = -1 = -f(x)$. Sedan får man undersöka de andra möjliga fallen på $x$.

Kan också hjälpa med en bild på funktionen:


(Tekniskt sett är funktionen inte udda i $x=0$, men för integralerna kvittar det helt då det endast är en punkt)

Aa ok men f är udda så blir ju fouriertransformen 0 från -a till a? Det låter som att funktionen är både udda och jämn. 

Så långt har jag kommit.

PATENTERAMERA skrev:

En funktion är udda om f(-x) = f(x) och jämn om f(-x) = f(x).

Ett skrivfel men vill bara förtydliga att det ska vara: 

Udda: f(-x)=-f(x)

Jämn: f(-x)=f(x)

På julafton måsta man låta udda vara jämnt.

destiny99 skrev:

Så långt har jag kommit.

Hur går jag vidare sen?

Nu kan du utnyttja inverstransformen. Vi vet ju att inversen skall ge tillbaka den ursprungliga funktionen. Kan du få fram den sökta integralen från inverstransformen? 

AlexMu skrev:

Nu kan du utnyttja inverstransformen. Vi vet ju att inversen skall ge tillbaka den ursprungliga funktionen. Kan du få fram den sökta integralen från inverstransformen? 

Ja , men hur ska man hantera gränserna 0 till inf ? Vi har dessutom sinbx.

Sinus-delen kommer dyka upp från eulers formel med faktorn $e^{i\omega x}$ och gränserna kommer in genom att notera att funktionen i den sökta integralen är jämn och därmed hälften av integralen över hela reella linjen. 

AlexMu skrev:

Sinus-delen kommer dyka upp från eulers formel med faktorn $e^{i\omega x}$ och gränserna kommer in genom att notera att funktionen i den sökta integralen är jämn och därmed hälften av integralen över hela reella linjen. 

Men hur ska man sätta upp detta? Jag trodde man var ute efter att räkna ut den integralen av uttrycket från 0 till inf. Den ser iförsig ganska  omöjlig ut.

Genom att direkt applicera inversfouriertransformen får vi att

$\displaystyle f\left(x\right)= \frac{1}{2\pi}\int_{-\infty}^\infty 2i\frac{\cos{a\omega}-1}{\omega}e^{i\omega x}d\omega$

Härifrån ger Eulers formel (och lite förenkling) 

$\displaystyle f\left(x\right) = \frac{i}{\pi}\int_{-\infty}^\infty \frac{\cos{a\omega}-1}{\omega}\cos\left(\omega x\right)d\omega - \frac{1}{\pi}\int_{-\infty}^\infty \frac{\cos{a\omega}-1}{\omega}\sin\left(\omega x\right)d\omega$

Nu för funktionerna i integranden, är någon udda? jämn?

AlexMu skrev:

Genom att direkt applicera inversfouriertransformen får vi att

$\displaystyle f\left(x\right)= \frac{1}{2\pi}\int_{-\infty}^\infty 2i\frac{\cos{a\omega}-1}{\omega}e^{i\omega x}d\omega$

Härifrån ger Eulers formel (och lite förenkling) 

$\displaystyle f\left(x\right) = \frac{i}{\pi}\int_{-\infty}^\infty \frac{\cos{a\omega}-1}{\omega}\cos\left(\omega x\right)d\omega - \frac{1}{\pi}\int_{-\infty}^\infty \frac{\cos{a\omega}-1}{\omega}\sin\left(\omega x\right)d\omega$

Nu för funktionerna i integranden, är någon udda? jämn?

Integranden till höger liknar den i uppgiften och den blir jämn pga hela integranden blir jämn kring symmetriskt intervall. Så vi får 2/pi från 0 till inf. Den enda integraden som är udda och överlever ej är den till vänster och den blir 0.

Japp! Då får vi alltså att

$\displaystyle f\left(x\right) = -\frac{2}{\pi}\int_0^{\infty} \frac{\cos a\omega - 1}{\omega}\sin\left(x\omega\right)d\omega$

Kan du avsluta härifrån?

PS, ett annat sätt att komma fram till att den första integralen är 0 är att den måste bli det, oavsett funktionen i integrandet. VL är reellt och integralen har faktorn $i$, vilket inte finns någon annanstans. Därmed måste integralen ha värdet 0 för att få bort $i$:et (oavsett om den är udda eller ej). 

AlexMu skrev:

Japp! Då får vi alltså att

$\displaystyle f\left(x\right) = -\frac{2}{\pi}\int_0^{\infty} \frac{\cos a\omega - 1}{\omega}\sin\left(x\omega\right)d\omega$

Kan du avsluta härifrån?

PS, ett annat sätt att komma fram till att den första integralen är 0 är att den måste bli det, oavsett funktionen i integrandet. VL är reellt och integralen har faktorn $i$, vilket inte finns någon annanstans. Därmed måste integralen ha värdet 0 för att få bort $i$:et (oavsett om den är udda eller ej). 

Nej jag vet inte hur man ska avsluta härifrån.

Tips. Sätt x = b i din formel och jämför med den integral som du enligt uppgiften skall räkna ut.

PATENTERAMERA skrev:

Tips. Sätt x = b i din formel och jämför med den integral som du enligt uppgiften skall räkna ut.

Du menar formeln jag fick i #16?

Formeln i #23.