Kriget mellan polymomfunktioner och potensfunktioner

... Varför heter denna post så?

Visa spoiler

Vår TA använde det och det var väldigt evokativt!

Jag vill kolla om dessa lösningarna duger. Så det heliga kriget ser ut såhär:

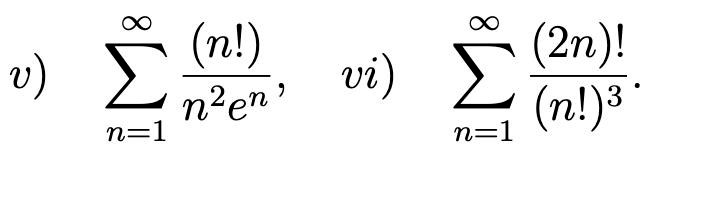
$\ln (x) \underset{v ä x e r l å n g s a m m a r e ä n}{< x^{p} < p^{x} < x! < x^{x}}$

Så i 5)an är dominerande termen x fakultet (efter att vi har konverterat serien till en integral), så serien kommer att divergera.

Däremot i 6)an jag undrar om vi kan använda oss av:

$n! \geq 2^{n - 1}$

och skriva: $\int \frac{(2 n)!}{n!^{3}} < \int \frac{(2 n)!}{(2^{n - 1})^{3}} < \int \frac{2 \cdot 2^{n - 1}}{(2^{n - 1})^{3}} = \int \frac{2^{n}}{2^{3 n - 3}} < \int \frac{1}{2^{2 n}}$

och den sista är konvergent, saken är pasta?

Jag är lite oklar på en av olikheten:

$\frac{(2n)!}{(2^{n-1})^3} < \frac{2="" \cdot="">$

som verkar antyda

$(2n)! < 2="" \cdot="" 2^{n="" -="">$

vilken inte stämmer eller läser jag det fel?

Rent generellt när man håller på med fakulteter brukar jag finna det hjälptsamt att skriva ut produktrepresentationer av fakultetern och sedan arbeta med de uttrycken.

Exempelvis kan man börja med

$\cfrac{(2n!)}{(n!)^3} = \cfrac{2n \cdots 2 \cdot 1}{(n \cdots 2 \cdot 1)^3} = \cfrac{(n + n) \cdots (n + 2)(n + 1)}{n^2 \cdots 2^2 \cdot 1^2}$

och sedan kan man se om det finns några manipulationer man kunde göra för att se om man kan hitta en övre begränsning.

Hej!

De icke-triviala olikheterna är

$\ln x < x^p=""><>$

medan det är självklart att $p^x <>$ om $p \leq x$ --- om $p>x$ så är det inte nödvändigtvis sant --- och det är lika självklart att $x! <>$ eftersom $x!$ är en produkt av heltal som alla är mindre än $x+1$ .

SeriousCephalopod och Albiki har gett bra förklaringar, men jag skulle vilja slå ett slag för kvottestet i detta fall:

$\lim_{n \to \infty} (\frac{a_{n + 1}}{a_{n}}) = \lim_{n \to \infty} \frac{(\frac{(2 (n + 1))!}{((n + 1)!)^{3}})}{(\frac{(2 n)!}{(n!)^{3}})} = \lim_{n \to \infty} \frac{(2 (n + 1))! \cdot (n!)^{3}}{((n + 1)!)^{3} \cdot (2 n)!} =$

$\lim_{n \to \infty} \frac{(2 n + 2) (2 n + 1)}{(n + 1)^{3}} = 0$

Gränsvärdet är mindre än ett, och därmed konvergerar serien. :)

Det blev en blodig krig igen!

Tack!

Andra sätt att lösa förutom kvotregel?

Jag får för övrigt inte min fakultetsomskrivning att fungera så den var nog en återvändsgränd.

Svara Avbryt

Visa senaste svar