Kva 2012 uppgift 18
 Hej! I denna uppgiften får jag svaret till A och förstår verkligen inte varför det inte är rätt. Jag får sidan AB till 50,5+4 vilket jag uppskattar till att vara större än 6.
Hej! I denna uppgiften får jag svaret till A och förstår verkligen inte varför det inte är rätt. Jag får sidan AB till 50,5+4 vilket jag uppskattar till att vara större än 6.
Tycker det är jättekonstigt?
Tacksam för hjälp!
Hur får du fram roten ur fem? :)
Smutstvätt skrev:Hur får du fram roten ur fem? :)
Hoppas du förstår min uträkning av sidan x där jag redovisar hur jag kom fram till värdet 50,5
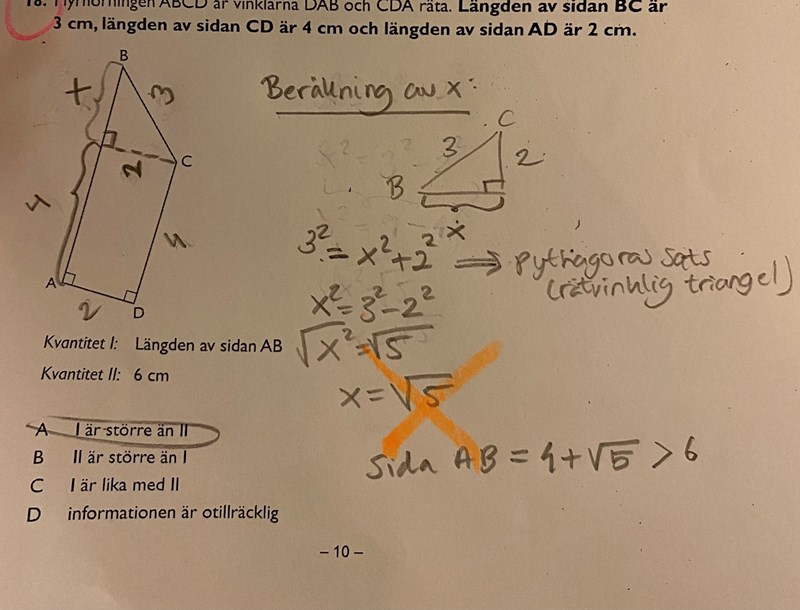
Vi vet inte egentligen om AB är längre än CD. Det är bara figuren som får oss att tro det. :)
Smutstvätt skrev:Vi vet inte egentligen om AB är längre än CD. Det är bara figuren som får oss att tro det. :)
Okej… då förstår jag absolut ingenting:/ Trodde verkligen jag gjorde rätt. Är detta en parallelltrapets? Är höjden i triangeln 2? Förstår inte…
Sidan AB kan ju vara kortare än CD även om figuren visar ngt annat.
Texten säger inte att figuren är den enda möjliga illustration av det som står i uppgiften
Ture skrev:Sidan AB kan ju vara kortare än CD även om figuren visar ngt annat.
Texten säger inte att figuren är den enda möjliga illustration av det som står i uppgiften
Men är det bäst då att inte kolla på den avtecknade figuren alls, eftersom det bara står fyrhörning i infon? Ska man istället försöka måla upp en figur på egen hand som stämmer in på beskrivningen?
Ja. Du kan utgå från figuren, men du måste vara medveten om vilken information vi får från uppgiften och inte. :)
Smutstvätt skrev:Ja. Du kan utgå från figuren, men du måste vara medveten om vilken information vi får från uppgiften och inte. :)
Förstår inte hur jag ska beräkna sidan AB? Kommer inte fram till någonting tyvärr:/… Skulle du vilja visa en uträkning på denna uppgiften? Det skulle vara mycket uppskattat!
Vi kan inte riktigt beräkna AB. Det vi har är följande figur:
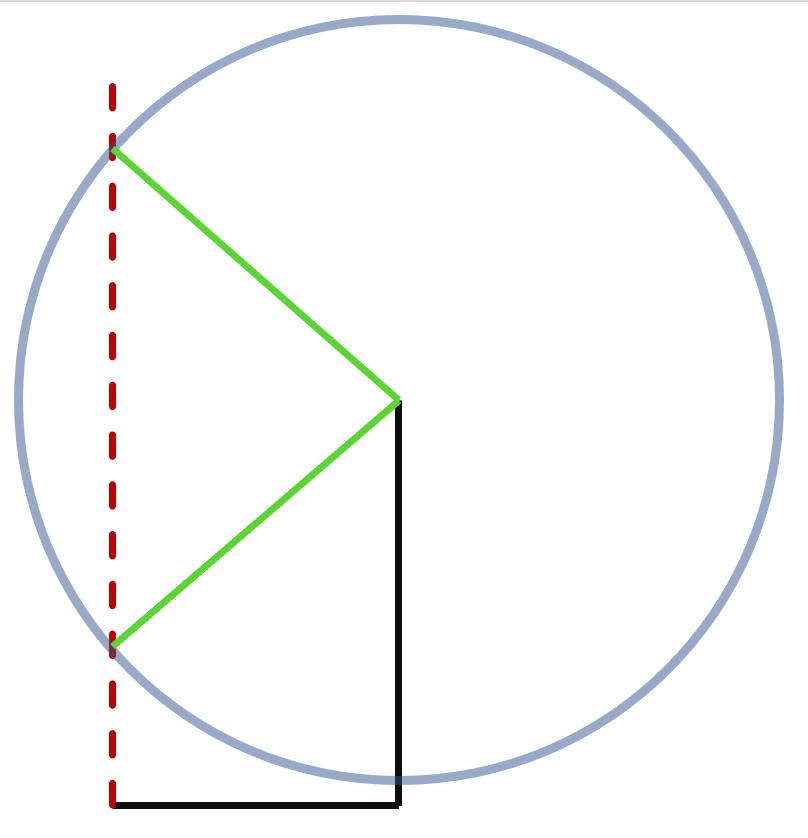
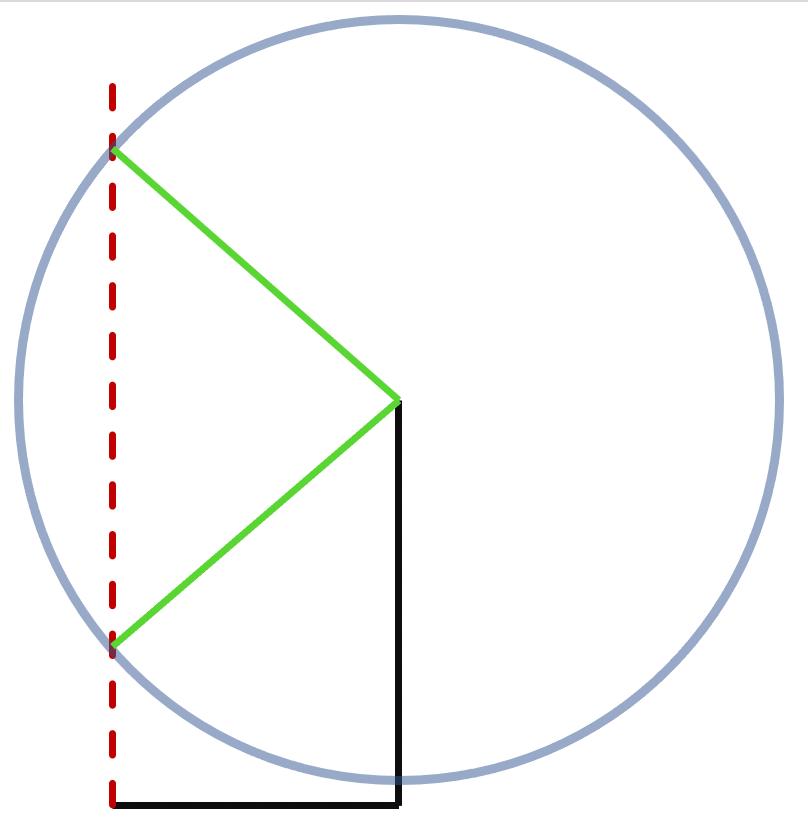
De svarta sträckorna är bestämda, och den streckade röda linjen är okänd. Vi vet även att BC är 3 cm, och därför kan BC (neongrön) ligga någonstans längs den blågråa cirkeln. Beroende på var kommer vinkeln vid C att förändras.
Eftersom ABCD är en fyrhörning, kan BC inte sticka ut utanför kanten AB, och det gör att vi får två möjliga figurer. Dessa två alternativ för BC är markerade med neongrönt i bilden ovan. :)
Smutstvätt skrev:Vi kan inte riktigt beräkna AB. Det vi har är följande figur:
De svarta sträckorna är bestämda, och den streckade röda linjen är okänd. Vi vet även att BC är 3 cm, och därför kan BC (neongrön) ligga någonstans längs den blågråa cirkeln. Beroende på var kommer vinkeln vid C att förändras.
Eftersom ABCD är en fyrhörning, kan BC inte sticka ut utanför kanten AB, och det gör att vi får två möjliga figurer. Dessa två alternativ för BC är markerade med neongrönt i bilden ovan. :)
Ja! Okej jag förstår, därmed är informationen otillräcklig eftersom sidan BC kan ha två olika placeringar, varav den ena resulterar i att AB blir större än 6 cm, och den andra resulterar i att AB blir mindre än 6 cm. Tack!
Helt rätt! Varsågod! :)
Vilken fantastiskt bra förklaring, Smutstvätt!