Kvadratisk approximation

Det borde stå något om kvadratisk approximation i din bok.

Om inte så kan du googla och du får då bland annat det här:

Nej, det står ingenting. Utifrån frågan ska jag bara fundera ut över hur man skulle kunna göra det utan att känna till det.. men det klarar jag inte av.

Jag skulle enligt facit utgå ifrån ax^2 +bx + c

Och redan kräva att f(x) = g(x)

F'(0) = g'(0)

F''(0) = g''(0)

Och på så vis resonera mig fram till svaret.

Jag hade aldrig någonsin listat ut det så tur jag skippade frågan.

Tack ändå.

Dkcre skrev:

F'(0) = g'(0)

F''(0) = g''(0)

Och på så vis resonera mig fram till svaret.

Jag hade aldrig någonsin listat ut det så tur jag skippade frågan.

Tack ändå.

Det är svårt att lista ut detta. Iden bakom det är att man väljer en baspunkt, i detta fall $x=0$ och där ska vår kvadratiska approximation vara som bäst. Det finns inget bättre än att vara helt exakt, så vi kräver $f(0) = g(0)$.

Men approximationen ska helst vara bra nära $x=0$, så om derivatan i denna punkt är samma så kommer funktionerna ungefär förändras på samma sätt (och därmed ungefär ha samma värden), därför kräver vi $f^'(0) = g^'(0)$, vilket ger oss tangentlinjen/linjärapproximationen.

Nästa steg är att derivatorna till funktionerna förändras ungefär på samma sätt, detta kommer i sin tur se till att funktionerna ändras på liknande sätt och där kommer $f^{''}(0) = g^{''}(0)$ in. Man kan också tänka sig att detta krav är som att vi linjärapproximerar derivatan.

En approximation nära x₀ = 0 ges nu av

$f(x)\approx f(0)+f'(0)\cdot (x-0)+\frac{f''(0)}{2}(x-0)^2$

Eftersom $f(0)=f'(0)=f''(0)=1$ så får vi

$f(x)\approx1+x+\frac{x^2}{2}$

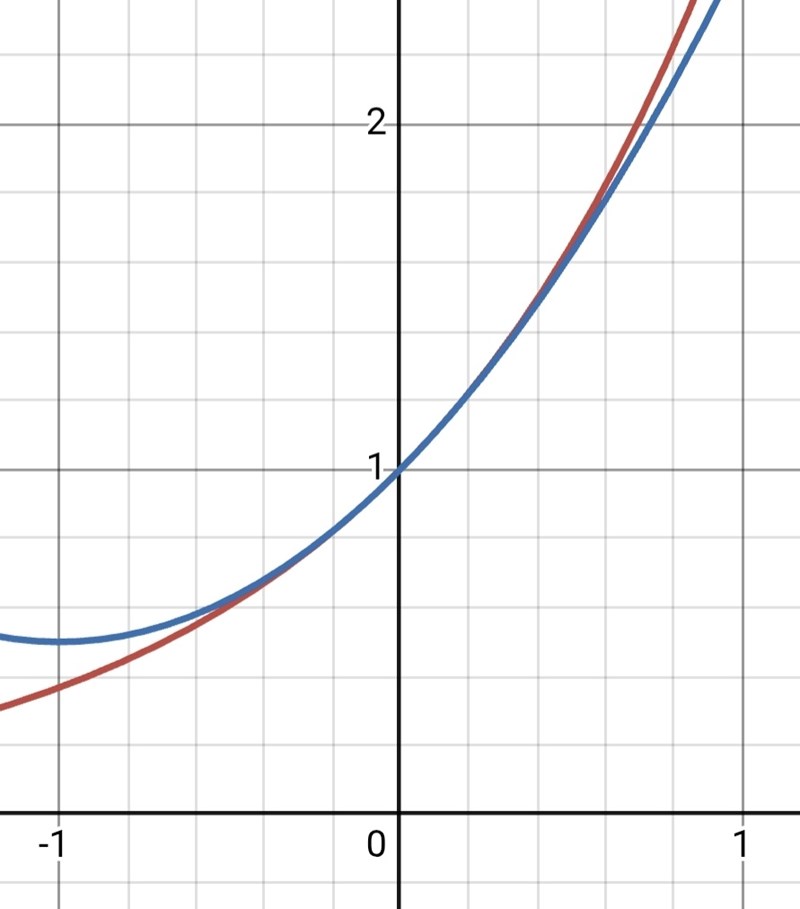
Använd gärna ngt grafritande program för att jämföra de två graferna med varandra nära x = 0.

Då får du detta:

Okej..

Tack