Kvadratiska mönster

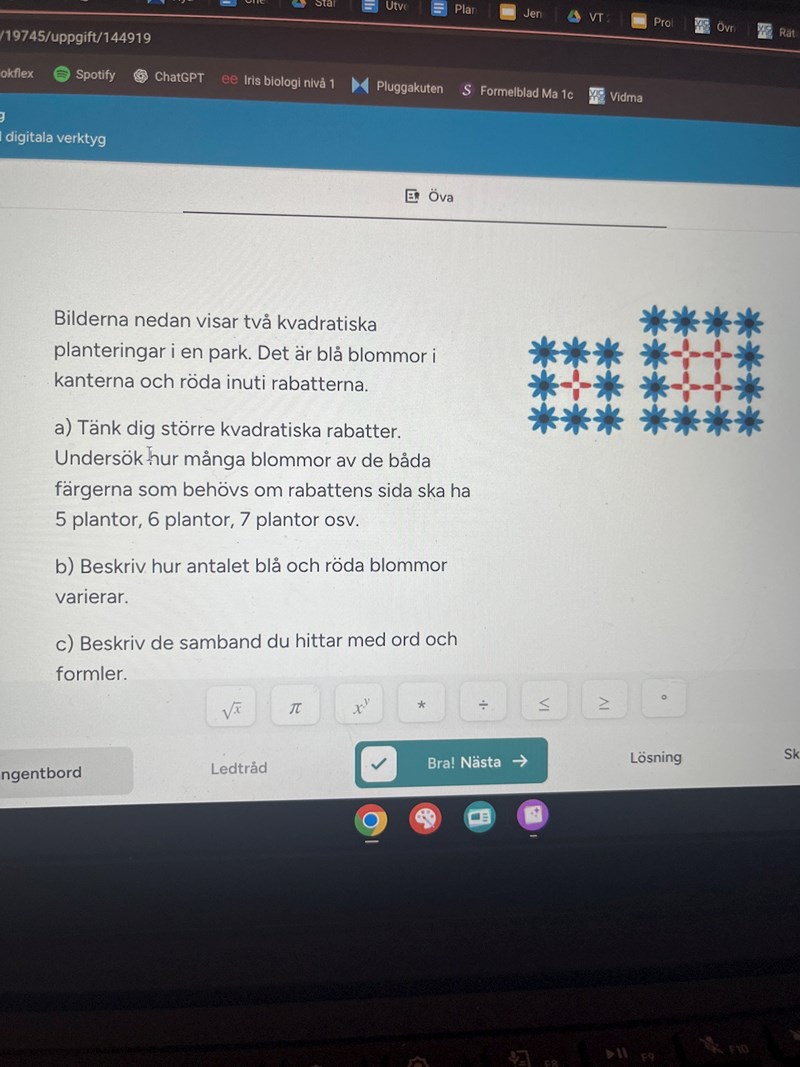
Börja med att bestämma antalet BLÅ blommor för varje typ av rabatt.

1a figuren är "3 plantor i kvadrat" = 3+2+3 = 3+(1)*2+3 blå plantor

2a figuren är "4 plantor i kvadrat" = 4+2+2+4 = 3+(2)*2+3 blå plantor

3e figuren är "5 plantor i kvadrat" = 4+2+2+2+4 = 3+(3)*2+3 blå plantor

4e figuren är "6 plantor i kvadrat" = 4+2+2+2+2+4 = 3+(4)*2+3 blå plantor

Kan du fnna ett uttryck för när det är  n  planter i kvadrat?

Om du tycker att figur 1 borde ha sidan 1, så kan du rita dit de två som fattas. Det är sidans längd som är intressant, inte figurernas nummer.

Trinity2 skrev:

Börja med att bestämma antalet BLÅ blommor för varje typ av rabatt.

1a figuren är "3 plantor i kvadrat" = 3+2+3 = 3+(1)*2+3 blå plantor

2a figuren är "4 plantor i kvadrat" = 4+2+2+4 = 3+(2)*2+3 blå plantor

3e figuren är "5 plantor i kvadrat" = 4+2+2+2+4 = 3+(3)*2+3 blå plantor

4e figuren är "6 plantor i kvadrat" = 4+2+2+2+2+4 = 3+(4)*2+3 blå plantor

Kan du fnna ett uttryck för när det är  n  planter i kvadrat?

Stämmer verkligen siffrorna för "5 plantor i kvadrat"  och "6 plantor i kvadrat" ?
Jag måste rita och kolla…   (även "4 plantor i kvadrat")

Arktos skrev:

Trinity2 skrev:

Börja med att bestämma antalet BLÅ blommor för varje typ av rabatt.

1a figuren är "3 plantor i kvadrat" = 3+2+3 = 3+(1)*2+3 blå plantor

2a figuren är "4 plantor i kvadrat" = 4+2+2+4 = 3+(2)*2+3 blå plantor

3e figuren är "5 plantor i kvadrat" = 4+2+2+2+4 = 3+(3)*2+3 blå plantor

4e figuren är "6 plantor i kvadrat" = 4+2+2+2+2+4 = 3+(4)*2+3 blå plantor

Kan du fnna ett uttryck för när det är  n  planter i kvadrat?

Stämmer verkligen siffrorna för "5 plantor i kvadrat"  och "6 plantor i kvadrat" ?
Jag måste rita och kolla…   (även "4 plantor i kvadrat")

Visa spoiler

"4 plantor i kvadrat" kräver  4² plantor varav 2² röda

"5 plantor i kvadrat" kräver  5² plantor varav 3² röda

"6 plantor i kvadrat" kräver  6² plantor varav 4² röda

Kan det vara något att bygga vidare på?

Jag tänkte att man delar upp det i blå och röda plantor. 

Trinity2 skrev:

 

1a figuren är "3 plantor i kvadrat" = 3+2+3 = 3+(1)*2+3 blå plantor

2a figuren är "4 plantor i kvadrat" = 4+2+2+4 = 3+(2)*2+3 blå plantor

3e figuren är "5 plantor i kvadrat" = 4+2+2+2+4 = 3+(3)*2+3 blå plantor

4e figuren är "6 plantor i kvadrat" = 4+2+2+2+2+4 = 3+(4)*2+3 blå plantor

Kan du fnna ett uttryck för när det är  n  planter i kvadrat?

Är det att figurens nummer multipliceras med 2.  I det fallet hade sambandet varit $6+n\left(2\right)$men det känns fel.

Abarnet skrev:

Trinity2 skrev:

 

1a figuren är "3 plantor i kvadrat" = 3+2+3 = 3+(1)*2+3 blå plantor

2a figuren är "4 plantor i kvadrat" = 4+2+2+4 = 3+(2)*2+3 blå plantor

3e figuren är "5 plantor i kvadrat" = 4+2+2+2+4 = 3+(3)*2+3 blå plantor

4e figuren är "6 plantor i kvadrat" = 4+2+2+2+2+4 = 3+(4)*2+3 blå plantor

Kan du fnna ett uttryck för när det är  n  planter i kvadrat?

Är det att figurens nummer multipliceras med 2.  I det fallet hade sambandet varit $6+n\left(2\right)$men det känns fel.

Sorry, Copy/Paste fel av mig!

Vi noterar att n:te figuren har n+2 (blå) plantor i kvadratens sida

Fig 1: 1+2=3 plantor i sidan

Fig 2: 2+2=4 plantor i sidan

osv.

Studera nu 2a figuren i din bild som får tjäna som mall. Notera att "toppen" och "botten" är = sidor och vi har

(n+2)+(n+2)=2(n+2) blå plantor.

Då kommer vi till de "mellanliggande" blå plantorna. Hur många sådana rader finns det?

De lodräta sidorna är också (likt toppen och botten) n+2 plantor, men vi skall inte räkna toppen och botten så vi får subrahera 2 och får n+2-2=n. Men det är n till vänster och n till höger, vilket totalt ger 2n.

Nu har vi totalt

2(n+2)+2n = 4(n+1) blå plantor

Vi testar

n=1 = 4*2=8 blå plantor - stämmer.

n=2 = 4*3=12 blå plantor - stämmer.

Det ser bra ut!

Alternativt. 

De blå plantorna bildar en ram runt "planteringen". Varje sida är 2 plantor mer än figurens ordningsnummer.

Fig 1 har 1+2=3plantor i sidan

Fig 2 har 2+2=3 plantor i sidan

Fig n har n+2 plantor i sidan.

Då vi har 4 sidor har vi alltså totalt 4(n+2) plantor MEN vi räknar 4 hörnplantor 2 gånger! Alltså är det 4(n+2)-4=4(n+1) enskilda, olika, plantor.

Fundera nu på hur du kan finna en formel för de röda plantorna. Rita en 3:e figur och det kommer att klarna, gör det inte det, rita en 4:e figur. 

Hoppas det ser tydligt ut! 

MYCKET BRA!

Tack för hjälpen!!!

Trinity2 skrev:

Arktos skrev:

Visa föregående citat

Trinity2 skrev:

Börja med att bestämma antalet BLÅ blommor för varje typ av rabatt.

1a figuren är "3 plantor i kvadrat" = 3+2+3 = 3+(1)*2+3 blå plantor

2a figuren är "4 plantor i kvadrat" = 4+2+2+4 = 3+(2)*2+3 blå plantor

3e figuren är "5 plantor i kvadrat" = 4+2+2+2+4 = 3+(3)*2+3 blå plantor

4e figuren är "6 plantor i kvadrat" = 4+2+2+2+2+4 = 3+(4)*2+3 blå plantor

Kan du fnna ett uttryck för när det är  n  planter i kvadrat?

Stämmer verkligen siffrorna för "5 plantor i kvadrat"  och "6 plantor i kvadrat" ?
Jag måste rita och kolla…   (även "4 plantor i kvadrat")

Visa spoiler

"4 plantor i kvadrat" kräver  4² plantor varav 2² röda

"5 plantor i kvadrat" kräver  5² plantor varav 3² röda

"6 plantor i kvadrat" kräver  6² plantor varav 4² röda

Kan det vara något att bygga vidare på?

Jag tänkte att man delar upp det i blå och röda plantor. 

Det tänkte jag också, men jag började med de röda:

"4 plantor i kvadrat" kräver  4² plantor
varav 2² röda och resten blå, dvs 4² - 2² 

"5 plantor i kvadrat" kräver  5² plantor
varav 3² röda och resten blå, dvs 5² - 3²

"6 plantor i kvadrat" kräver  6² plantor
varav 4² röda och resten blå, dvs 6² - 4²

etc

"n plantor i kvadrat" kräver  n² plantor
varav (n-2)² röda och resten blå, dvs n² - (n-2)²
som kan förenklas till
n² - ( n² - 4n + 4) = 4n - 4 = 4(n - 1)

Man får rita och kolla  :-)