Kvadratkomplettering

Om första termen skall vara en kvadrat så är det (2x) som man har kvadrerat.

Andra termen är (2x) * 10

Rättning: Andra termen är (2x) * (-10)

Det vore bra om du skrev vad du fått för svar och hur du gjort. På så sätt kan man någorlunda identifiera vad som gått snett.

"Hur har du tänkt?" är en viktig fråga som underlättar när man försöker formulera ett svar på hur du skall tänka.

Kan bifoga en bild på hur jag har tänkt.

Om du skrev ut vad som skulle fås ur

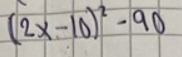
m.h.a. kvadreringsregeln, så skulle du se att det inte stämmer:

$(2x-10)^2-90=(2x)^2-2\cdot2x\cdot10+10^2-90=4x^2-{\color[rgb]{0.7, 0.0, 0.0}40}x+10$

Kvadreringsregeln lyder $(A-B)^2 = {\color[rgb]{0, 0.7, 0}A^2} - {\color[rgb]{0, 0, 0.7}2AB} + {\color[rgb]{0, 0.5, 0.5}B^2}$. När den tillämpas baklänges på uttrycket ${\color[rgb]{0, 0.7, 0}4x^2} - {\color[rgb]{0, 0, 0.7}20}x + 10$, så ser du att:

• ${\color[rgb]{0, 0.7, 0}A^2 = 4x^2}$, så $A = 2x$.
• ${\color[rgb]{0, 0, 0.7}2AB = 20x}$ och man redan vet att $A=2x$, så $2 \cdot 2x \cdot B = 20x$, vilket ger att $B=5$
• Det är alltså ${\color[rgb]{0, 0.5, 0.5}B^2 = 5^2} = 25$ som behöver läggas till och subtraheras för att komplettera kvadraten