Kvantmekanik - Oändlig lådpotential
Hej! Hur går jag tillväga på denna uppgift?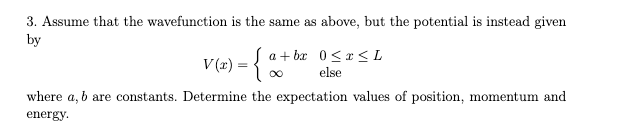
Jag vet hur man ska göra om potentialen är noll i intervallet , men ej annars.
Vågfunktionen är också känd.
Det är samma vågfunktion, så det blir samma väntevärde för x .
Det är en partikel i en låda så väntevärde för rörelsemängd måste vara noll.
Väntevärde för energi är lite svårare. Man ska i alla fall addera konstanten a. Sedan beror det på hur vågfunktionen ser ut.
Det är samma vågfunktion, så det blir samma väntevärde för x .
Det var det jag anade, är det bara för att ? Gäller det alltid att vätnevärdet är samma? Verkar som det enligt def, men osäker.
Det är en partikel i en låda så väntevärde för rörelsemängd måste vara noll.
I fallet då för , så fick jag ett väntevärde för rörelsemängden som var nollskilt, och i det fallet är det väl också en partikel i en låda? Varför blir väntevärdet 0?
Väntevärde för energi är lite svårare. Man ska i alla fall addera konstanten a. Sedan beror det på hur vågfunktionen ser ut.
Vågfunktionen ges av , där n=1,3,5 där är de standard stationära tillstånden.
Borde det inte gå att använda ?
Klassiskt är en partikel i en låda en kula som studsar fram och tillbaka mellan två hårda väggar. Därför tror jag att väntevärdet av rörelsemängd måste vara noll.
I en sådan superposition blir det en sannolikhetstäthet som skvalpar fram och tillbaka. Typ så här:

https://commons.Wikimedia.org/wiki/File:Particle_in_a_box_(time_evolution).gif
Väntevärdet för positionen är att den ligger mitt i lådan när det är samma vågfunktion som innan den osymmetriska potentialen. Det är inte realistiskt så det är inget stabilt tillstånd. Potentialen kommer att blanda in andra termer i vågfunktionen. Men det behövde man alltså inte bry sig om i den här uppgiften.
Väntevärdet för positionen är att den ligger mitt i lådan när det är samma vågfunktion som innan den osymmetriska potentialen. Det är inte realistiskt så det är inget stabilt tillstånd. Potentialen kommer att blanda in andra termer i vågfunktionen. Men det behövde man alltså inte bry sig om i den här uppgiften.
Hur gör man för energin?
Hur gjorde du uppgiften innan?
Enklast är nog medelvärdet av energierna av dessa tre egentillstånd.
Här måste man i alla fall addera a. För termen med bx finns nog också en genväg. Alternativet är att använda definitionerna.
Pieter Kuiper skrev:Hur gjorde du uppgiften innan?
Enklast är nog medelvärdet av energierna av dessa tre egentillstånd.
Här måste man i alla fall addera a. För termen med bx finns nog också en genväg. Alternativet är att använda definitionerna.
Återkommer med energin. Jag insåg att jag hade gjort fel med rörelsemängden, nu när jag räknar ut det får jag 0.
Ser det ut att stämma?
Det här är länge sedan för mig men för väntevärdet av x2 hade jag förväntat mig ett uttryck som inte beror på tid, bara på L2.
Pieter Kuiper skrev:Det här är länge sedan för mig men för väntevärdet av x2 hade jag förväntat mig ett uttryck som inte beror på tid, bara på L2.
Hmm, tror inte riktigt jag hänger med på varför? Tiden hamnar ju som en konstant när man integrerar i positionen och då kommer den alltid vara med väl?
För väntevärdet av x fann du L/2 och det är säkert rätt.
På samma sätt förväntar jag något med endast L2 för väntevärdet av x2.
För grundtillståndet är det en standarduppgift att räkna ut det. Och Delta x. Och att jämföra med Heisenbergvillkoret.
Pieter Kuiper skrev:För väntevärdet av x fann du L/2 och det är säkert rätt.
På samma sätt förväntar jag något med endast L2 för väntevärdet av x2.
För grundtillståndet är det en standarduppgift att räkna ut det.
För att väntevärdet av x2 ska bli 0 så måste integralerna med , bli 0, vilket de inte blir när man multiplicerar dessa med x2 istället för bara x.
Men ska dubbelkolla mina räkningar
Självklart är <x2> inte noll.
Oj, menade såklart att väntevärdet av x2 endast beror på L2.
Här är facit för en annan liknande uppgift, med samma potential och liknande vågfunktion. Här blir det ej tidsoberoende.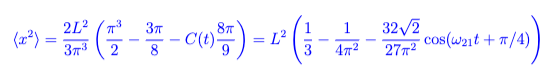
Ok, superpositionen inget stationärt tillstånd förstås, det ”skvalpar”.
Här måste man i alla fall addera a. För termen med bx finns nog också en genväg. Alternativet är att använda definitionerna.
Menar du såhär?
Det låter ju rimligt men som sagt, det här är länge sedan för mig.
Tror du man kan göra såhär ?
Det skulle jag i alla fall chansa på :)
Hur gör jag på denna?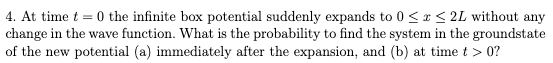
De säger att vågfunktionen är oförändrad, men om lådpotentialen ökar med L, så kommer väl vågfunktionen också se annorlunda ut eller?
Man beräknar överlapp med de nya egenfunktionerna.
Samma för (a) och (b) tror jag.
Jag har faktiskt skrivit en artikel om något liknande: https://pubs.aip.org/aip/jcp/article/100/6/4087/182003/The-absorption-peak-at-the-oxygen-1s-edge-of-O2
Länge sedan alltså.
Pieter Kuiper skrev:Man beräknar överlapp med de nya egenfunktionerna.
Samma för (a) och (b) tror jag.
Jag har faktiskt skrivit en artikel om något liknande: https://pubs.aip.org/aip/jcp/article/100/6/4087/182003/The-absorption-peak-at-the-oxygen-1s-edge-of-O2
Länge sedan alltså.
Coolt! Ja 1994 sen var inte igår hahah.
Är följande resonemang korrekt?
Expansionen sker ögonblickligt är densamma, däremot så ändras basen för vågfunktionen och ges istället av .
Sannolikheten ges av , där c1 fås från den inre produkten . Detta blir samma för a och b.
Den nya basen blir alla egenfunktioner av den större lådan. Alltså n=1,2,3,4 osv.
Så det blir vågfunktionen projicerat på.
För molekyler ger det https://en.wikipedia.org/wiki/Franck-Condon_principle
Hmm, förstår inte riktigt varför det blir så men det behövs väl egentligen inte heller för beräkningarna?
Uppgiften vara bara att räkna ut sannolikheten för den större lådans grundtillstånd, så det är inte så mycket jobb nej.


