Kvotrummet linjär algebra fk
Hej!
Jag förstår att kvotrummet definieras som V/W=[v] , men jag saknar en intuition gällande begreppet samt vad den där [v] menas med. Jag förstår det som att alla vektorer i V divideras med alla vektorer i W när jag ser divisionen.
Nja, så här är det.
[v] = {uV: u - vW}
V/W = {[v]: vV}
Tillägg: 4 nov 2025 20:29
PATENTERAMERA skrev:Nja, så här är det.
[v] = {uV: u - vW}
V/W = {[v]: vV}
Varför subtraherar man två vektorer i olika vektorrum? Varför adderar man inte inte dem? Sen förstår jag inte vad varför vi får [v] i båda fallen? Vad betyder [v]={u€V:u-v€W}samt V/W={[v]:v€V}?
W är ett underrum till V så det går bra att subtrahera.
PATENTERAMERA skrev:W är ett underrum till V så det går bra att subtrahera.
Vad innebär det att W är ett underrum till V och varför adderar man inte v och u? Jag förstår inte din bild. Jag förstår inte de här fallen heller
Det är samma sak som delrum, om det är en mer bekant term.
Subspace på engelska.
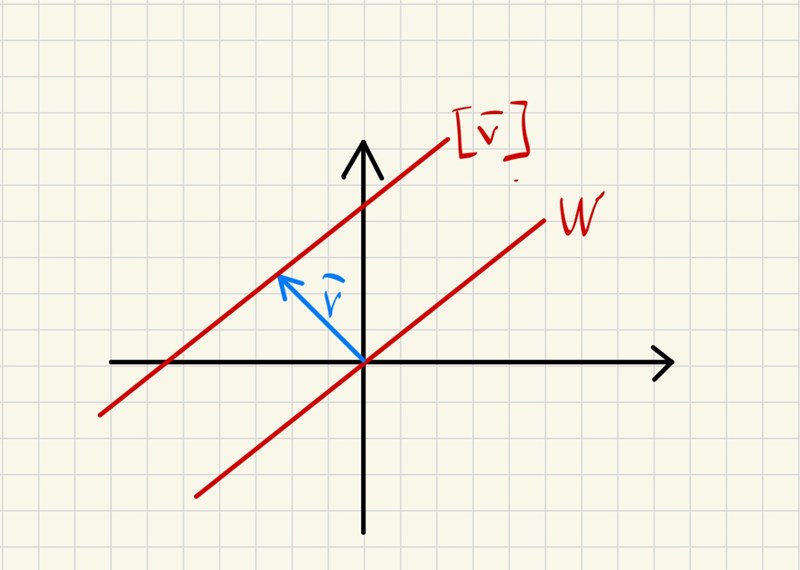
Detta är hur man definierar [v]. Om vi, som ett specialfall, ser W som en linje genom origo, så är [v] en linje som är parallell med W men som går genom v:s spets - se min figur.
PATENTERAMERA skrev:Det är samma sak som delrum, om det är en mer bekant term.
Subspace på engelska.
Detta är hur man definierar [v]. Om vi, som ett specialfall, ser W som en linje genom origo, så är [v] en linje som är parallell med W men som går genom v:s spets - se min figur.
Ok. Så alla vektorer som är parallella med W så utgör de en kvotrum dvs det blir vektorer sig själva?
Ja, om vi tänker oss W som en linje, så är V/W mängden av alla linjer som är parallella med W.
PATENTERAMERA skrev:Ja, om vi tänker oss W som en linje, så är V/W mängden av alla linjer som är parallella med W.
Ok jag förstår. Är det ett krav att W måste vara en linje som går genom origo för att linjerna ska vara parallella med W? Går det emot defintionen av V/W om denna W inte är en linje som går genom origo?
Nej, W kan vara ett delrum av godtycklig dimension. Om det är ett tvådimensionellt delrum så kan du se det som ett plan genom origo och V/W som mängden av alla plan som är parallella med W.


