Laboration i R: Normal- och exponentialfördelade slumptal
Hej,
Jag håller just nu på att lösa en uppgift i R och skulle behöva hjälp att tolka svaret. Jag kommer i detta inlägg visa min kodning, histogrammet samt vad själva frågan som ska besvaras är.
Uppgiften: I frågan har jag N(m,s2)-fördelade slumptal (antar i normalfördelningen?) samt n stycken exponentialfördelade slumptal med väntevärde 1/a och av dessa ska jag göra två histogram.
Besvara: Jag ska med hjälp utav R lösa om talen ser normal - respektive exponentialfördelade ut och besvara frågan om jag jämför detta med en fördelningsfunktion eller en täthetsfunktion. Jag ska även ange parametrarna m, s och a.
Här har jag redan löst första delen, jag ansatte som är väntevärdet, som är standardavvikelsen vilket ger som är variansen och till sist som är intensiteten.
Min kodning är följande:

där har jag även ansatt n till 1000 för båda histogrammen.
Histogramen:
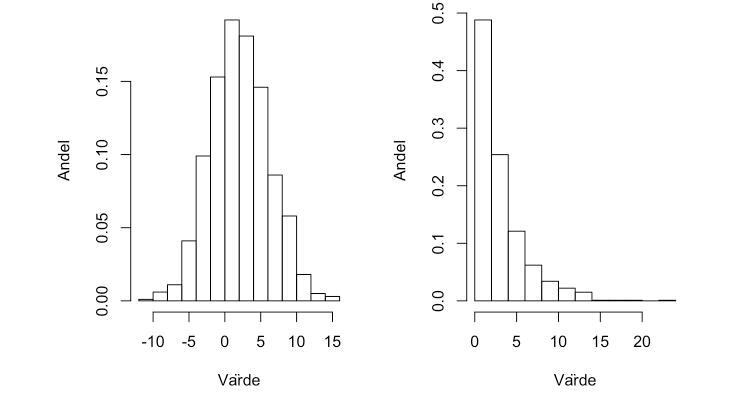
Och nu ska jag alltså tolka om de ser normal - respektive exponentialfördelade ut. Den normalfördelade visas till vänster och den exponentialfördelade till höger. Hur ska jag göra detta och hur vet jag om detta jämförs med en fördelning - eller täthetsfunktion?
Tack på förhand!
En första grej: sd = standard deviation = standardavvikelsen. Du säger i texten att du vill ha standardavvikelsen 2 men i koden har du skrivit sd = 4.
Men men, det är enkelt fixat. För att svara på din fråga:
Funktionen dnorm returnerar fördelningsfunktionen för normalfördelningen. För att lösa din uppgift kan du därför exempelvis göra en sekvens tal x som startar på det minsta värdet du genererat och slutar på det största med tex 0.1 i mellanrum (du skulle alltså behöva spara undan talen du genererar). Sedan kan du plotta dnorm(x,mean,sd) över ditt histogram med hjälp av funktionen "lines". Det skulle alltså bli ungefär såhär:
y = rnorm(1000,2,2) #spara genererade tal
prop_hist(y) #plotta histogram av genererade talen
x = seq(min(y),max(y),0.1) #skapa sekvens från min(y) till max(y) i steg om 0.1
lines(x,dnorm(x,2,2),col='red') #plotta fördelningsfunktionen ovanpå histogramet
På samma sätt kan du använda dexp för exponentialfördelningen
Hondel skrev:En första grej: sd = standard deviation = standardavvikelsen. Du säger i texten att du vill ha standardavvikelsen 2 men i koden har du skrivit sd = 4.
Men men, det är enkelt fixat. För att svara på din fråga:
Funktionen dnorm returnerar fördelningsfunktionen för normalfördelningen. För att lösa din uppgift kan du därför exempelvis göra en sekvens tal x som startar på det minsta värdet du genererat och slutar på det största med tex 0.1 i mellanrum (du skulle alltså behöva spara undan talen du genererar). Sedan kan du plotta dnorm(x,mean,sd) över ditt histogram med hjälp av funktionen "lines". Det skulle alltså bli ungefär såhär:
y = rnorm(1000,2,2) #spara genererade tal
prop_hist(y) #plotta histogram av genererade talen
x = seq(min(y),max(y),0.1) #skapa sekvens från min(y) till max(y) i steg om 0.1
lines(x,dnorm(x,2,2),col='red') #plotta fördelningsfunktionen ovanpå histogramet
plot(x,dnorm(x,2,2),type='l')På samma sätt kan du använda dexp för exponentialfördelningen
Jag inser att plotta fördelningsfunktionen ovanpå inte kommer riktigt stämma alltid, så det är nog bättre att bara plotta fördelningsfunktionen och jämföra med histogrammet

