Läges & rörelseenergin

Ja det stämmer.

Det bollen förlorar i lägesenergi vinner den i rörelseenergi.

Alltså 

mgh + m*0^2/2 = m*v^2/2 

Varför gäller det här sambandet? Kan man illustrera en bild?

Den totala mekaniska energin innan den faller: $E0=E0_p+E0_k$. Eftersom den är i vila vid start så är $E0_k=0$, vilket betyder att $E0=E0_p$

Den totala mekaniska energin när den fallit en meter $E1=E1_p+E1_k$

Det står ingen om luftmotstånd så vi bortser från det. Det betyder att den mekaniska energin är konstant under hela fallet, dvs att $E0=E1$.

Det ger dig ekvationen $E0_p=E1_p+E1_k$, dvs $E1_k=E0_p-E1_p$.

Med $E1_k=\frac{mv_1^2}{2}$, $E0_p=mgh_0$ och $E1_p=mgh_1$ så får vi att

$\frac{mv_1^2}{2}=mgh_0-mgh_1$

$\frac{mv_1^2}{2}=mg(h_0-h_1)$

Eftersom fallhöjden är 1 meter så är $h_0-h_1=1$:

$\frac{mv_1^2}{2}=mg\cdot1$

Och så vidare.

Blev det tydligare då?

Yngve det blir ganska svårt för mig att förstå vad E0 är, E0p och E0k . Det vore bättre om du skrev ut rörelseenergi istället för E0k , lägesenergi istället för E0p.. Jag upplever att det blir svårare att hänga med uträkningen

-

Jag hänger med på din uträkning framtills de första 2 radena , allt som står under förstår jag inte helt riktigt 

Kalla startpunken för A och punkten 1 meter längre ner för B. A har höjden h och B har höjden h-1.

Vid A är bollen i vila och dess mekaniska energi består då enbart av lägesenergi som är $mgh$.

Vid B består bollens mekaniska energi dels av lägesenergin $mg(h-1)$ och dels av rörelseenergin $\frac{mv^2}{2}$.

Eftersom den mekaniska energin hela tiden är konstant så gäller det att $mgh=mg(h-1)+\frac{mv^2}{2}$

Det innebär att $\frac{mv^2}{2}=mgh-mg(h-1)$, dvs $\frac{mv^2}{2}=mg$, dvs $$v^2=\frac}{g}{2}$$.

Skulle du kunna förklara det med hjälp av en bild? Det skulle vara mycket enklare att förstå? 
Jag förstår dina beräkningar men det vore bättre om du kunde förklara med hjälp av en bild :)

vi vet att m=8g

h=? 
Vad ska ”v” vara?

Det spelar ingen roll vad h är. Vi kan säga att h = 10 meter. Det som efterfrågas är v, vilket är hastigheten vid punkten B.

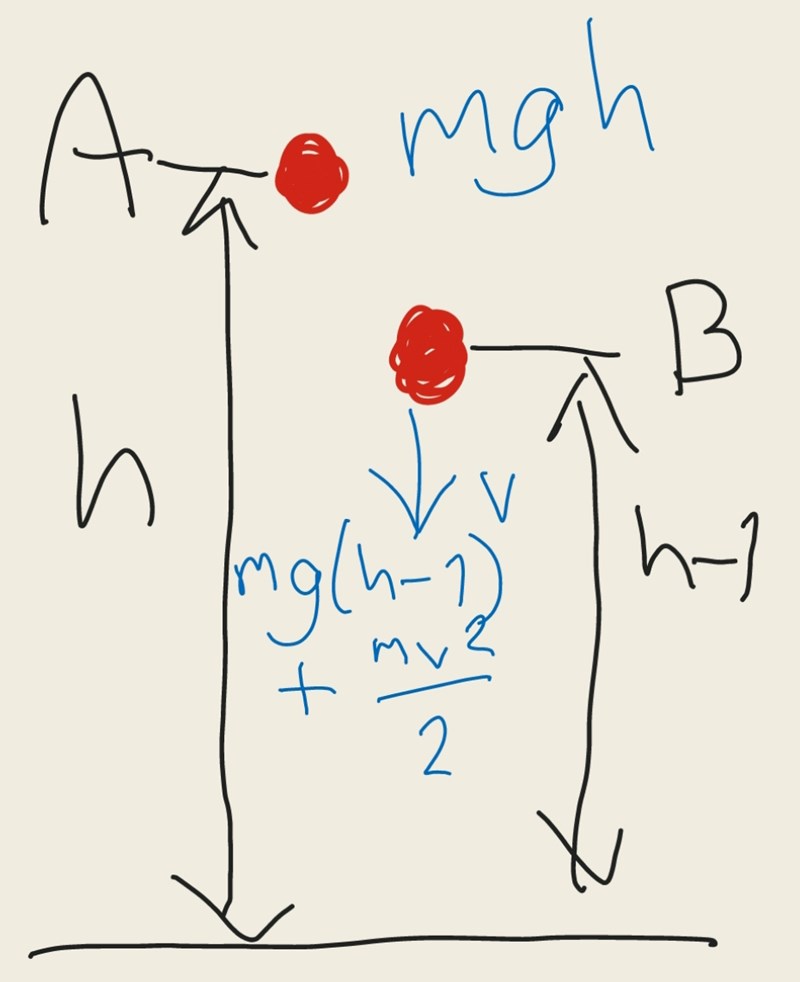
Varför är bollen i vila vid punkten A? 

Jag har en uppgift som går ut på att räkna ut vilken hastighet en boll har efter att ha fallit en meter från vila. 

Okej. 
Alltså gäller det att 

mgh=mg(h-1) + (1/2*mv^2) 

0.08kg*9.82*h=0.08kg*9.82*(h-1) + (1/2*0.08kg*v) 

Vi antar att h=10m 

isf blir v~4.4m/s

Varför spelar det ingen roll vilken höjd man sätter?

Svaret är rätt, men du råkade skriva $v$ istället för $v^2$ på ett ställe.

I själva verket spelar varken höjden $h$ eller massan $m$ någon roll i just det här fallet.

Bollen får samma hastighet oavsett om den faller ftån 10 till 9 meter eller om den faller från 67 till 66 meter. Prova själv i ekvationen så ser du att det stämmer.

Bollen får samma hastighet oavsett om den väger 8 gram eller om den väger 73 gram. Prova själv i ekvationen så ser du att det stämmer.

====================

Det blir tydligt om du börjar med att lösa ekvationen utan att sätta in siffervärden:

$mgh=mg(h-1)+\frac{mv^2}{2}$

Multiplicera in $mg$ i parentesen:

$mgh=mgh-mg\cdot1+\frac{mv^2}{2}$

Subtrahera $mgh$ från båda sidor:

$0=-mg+\frac{mv^2}{2}$

Addera $mg$ till båda sidor:

$mg=\frac{mv^2}{2}$

Dividera båda sidor med $m$:

$g=\frac{v^2}{2}$

Multiplicera båda sidor med 2:

$2g=v^2$

Dra roten ur båda sidor:

$v=\sqrt{2g}$

I detta uttryck för hastigheten finns varken $h$ eller $m$ med, alltså beror hastigheten $v$ varken på höjden $h$ eller massan $m$.