Läsa ut t (tiden)

sinus är en funktion, och kan inte stå ensam på det sättet. Det är ungefär som att skriva $\frac{15}{20\sqrt{}}$. Istället, ta arcsinus (eller sin^-1 som det kan stå på miniräknaren) av båda led. :)

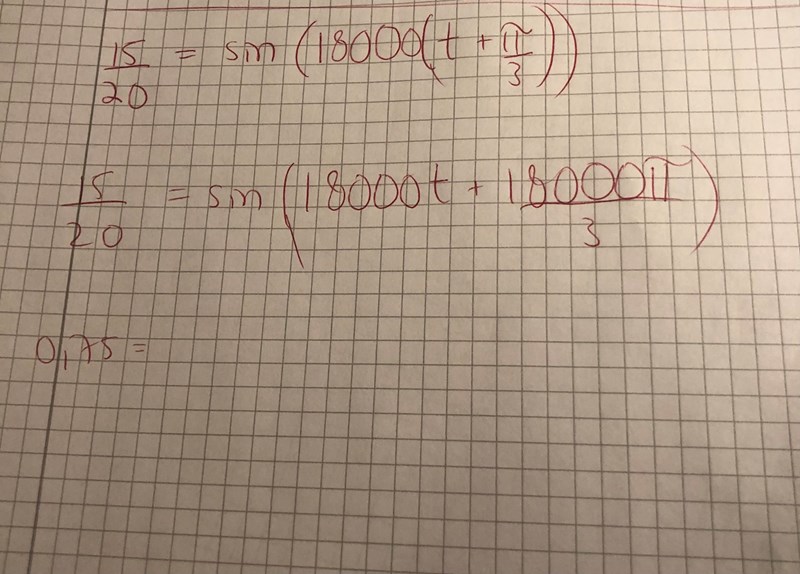Så här?

$\frac{15}{20}=\sin \left(18000\right(t+\frac{\mathrm{\pi }}{3}\left)\right)$

Beräkna arcsin(15/20). Det ska vara lika med $18000(t+\frac{\mathrm{\pi }}{3}) + 2\mathrm{\pi n} , \mathrm{n}\in \mathrm{\mathbb{Z}}$.
(I detta fall är det oväsentligt att ha med $2\mathrm{\pi n}$ som beskriver perioden. Sedan behöver vi inte bry oss om sinus som har två lika värden. Du ska bara ta reda på mista värdet på t)

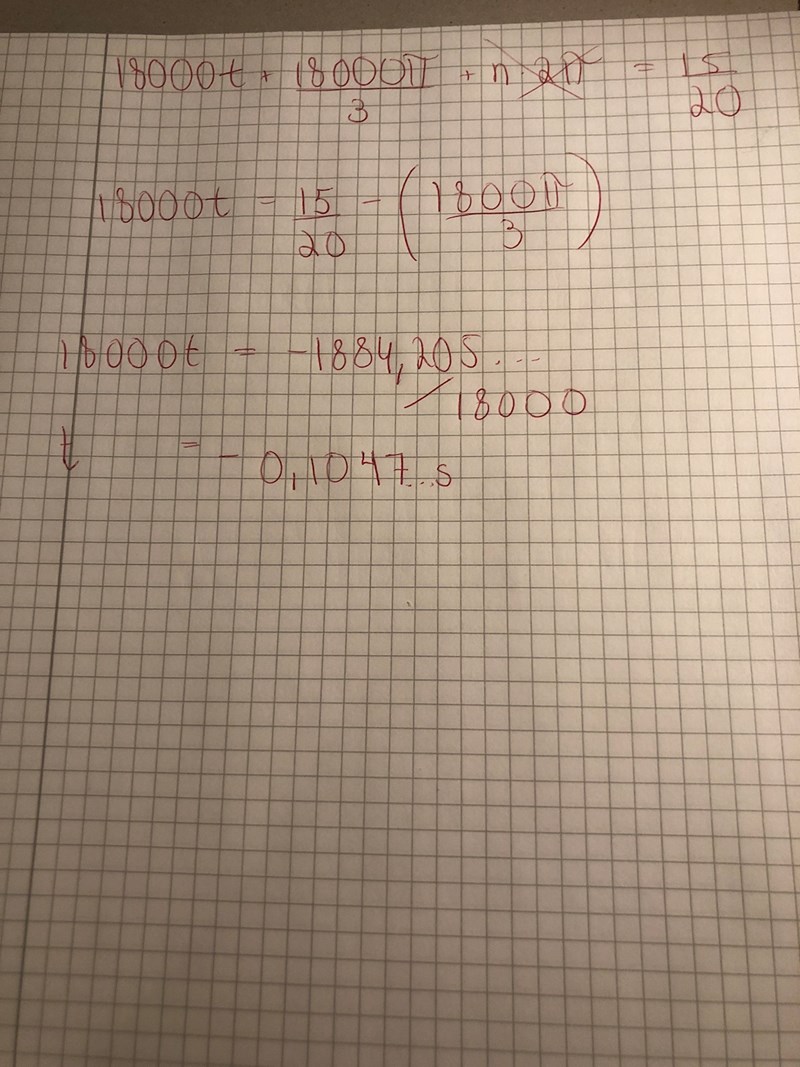något är knasigt i uträkningarna.

Du glömmer att ta arcsin av $\frac{15}{20}$.

Ekvationen är

$\frac{15}{20}=\sin(18000(t+\frac{\pi}{3}))$

Arcsin på båda sidor ger nu

$\arcsin(\frac{15}{20})=18000(t+\frac{\pi}{3})+n\cdot2\pi$

och

$\arcsin(\frac{15}{20})=\pi-18000(t+\frac{\pi}{3})+n\cdot2\pi$

Kommer du vidare då?

Ska man skippa n2pi?

Du kan antingen resonera dig fram till om du kan skippa n•2pi och lösningen "pi minus ..." eller så kan du ta det säkra före det osäkra och helt enkelt hitta den lösning som ger det lägsta positiva värdet på t.

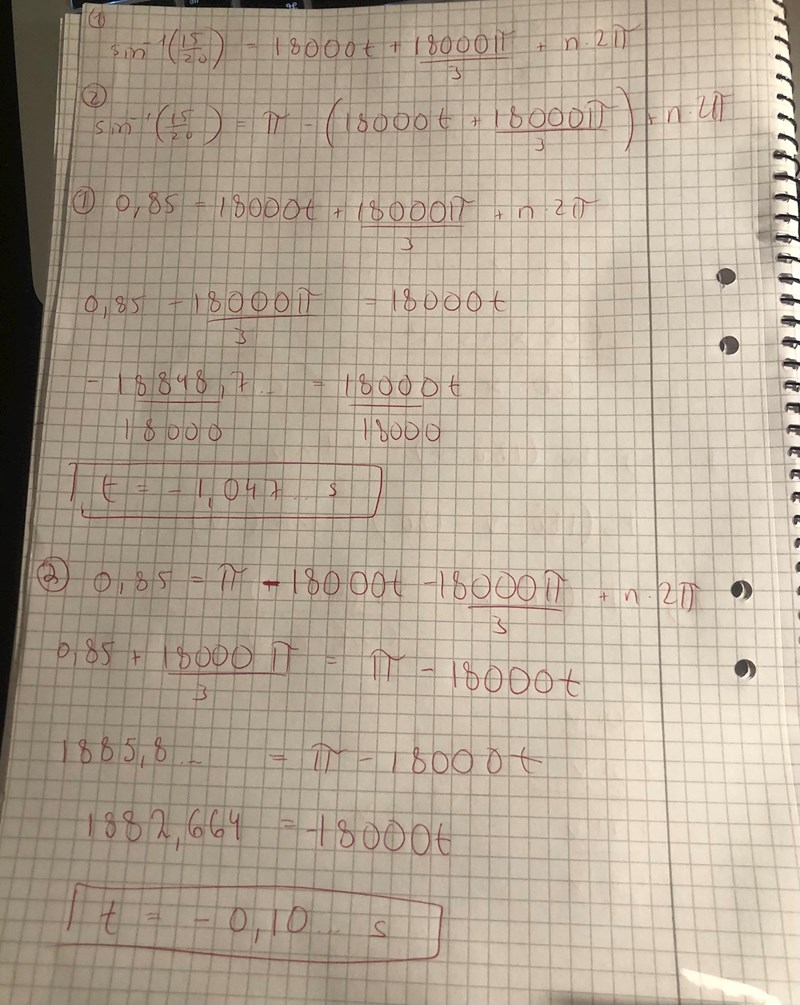Detta känns fel :(