Likformighet
Hej! Det är en uppgift om likformighet där jag skall bestämma sträckan CD.
Det känns som att jag tänker rätt och har försökt lösa ut men jag brister i något moment då jag inte kommer fram till det exakta svaret skulle jag kunna få lite vägledning. Tack på förhand!
Uppgiften: 
(min ansats/tankar)-
Först och främst tänker jag att trianglarna ABD och ADE är samma då de har gemensamma vinklar även längder.
Via triangeln ADE kan jag lösa ut AE som är en del av AC. Vilket är via Pythagoras sats.
triangel( CDE gäller detta) Därefter kan jag sätta det beräknade värdet som + y och räkna ut y via likformighet och när jag får fram basen behöver jag den andra kateten(höjden) vilket är DE alltså 3 och återigen med Pythagoras sats kan jag lösa ut DC.
Det känns som att jag tänker rätt och har försökt lösa ut men jag brister i något moment då jag inte kommer fram till det exakta svaret skulle jag kunna få lite vägledning. Tack på förhand!
ADE är kongruent med ADB.
Ja exakt de är kongruenta stämmer därav min tankegång?
Hur kan jag ta mig vidare?
Ja såklart AB och AE = 4 via Pythagoras sats men hur kommer jag vidare?!?!
Kan man säga något om vinkeln C?
Vet inte riktigt möjligtvis 2v ? Men triangeln är inte likbent alltså ABC
Nej, inte dubbla vinkeln av den som är markerad i figuren.
Gissa inte, ägna lite tid åt frågan om det går att säga något om vinkeln vid C.
Yttervinkelsatsen kan ge summan av de motstående vinklarna
isåfall c= 180-90- vinkel med ett streck
om vinkel med streck är 45 kommer även C att bli så?
- känns som att jag rör ihop det 🤦🏽♀️
Pieter Kuiper skrev:ADE är kongruent med ADB.
Då är alltså även de gröna vinklarna lika: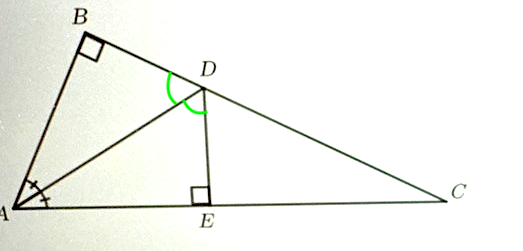
(Stämmer uppgiften egentligen, börjar jag undra...)
Hur ska det hjälpa? De vinklarna blir samma då det är likformighet som
gäller men jag kan inte riktigt se hur det kan hjälpa för att förstå vinkel c
Jag tror att det kanske finns ett problem. Om jag använder vinklarna i en 3:4:5 triangel får jag detta: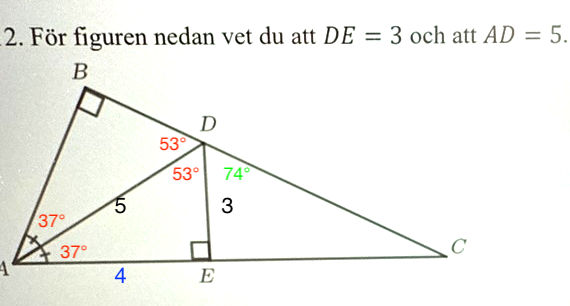
Och då kan jag inte se hur det går ihop.
Pieter Kuiper skrev:Jag tror att det kanske finns ett problem. Om jag använder vinklarna i en 3:4:5 triangel får jag detta:
Och då kan jag inte se hur det går ihop.
Det gör det inte heller!
Man kan förstås få ut att CD≈10,7 om man sätter ABC kongruent med CDE.
Verkligheten är dock en annan: EC > 2,5AE och ∠C≈16°.
Ja det stämmer att CD ska vara 10, 7, hur kom du fram till det?
jag tror att man skall lösa med likformighet och behöver inte vinklarnas värde
sictransit skrev:Pieter Kuiper skrev:Jag tror att det kanske finns ett problem. Om jag använder vinklarna i en 3:4:5 triangel får jag detta:
Och då kan jag inte se hur det går ihop.
Det gör det inte heller!
Man kan förstås få ut att CD≈10,7 om man sätter ABC kongruent med CDE.
Likformig.
Jag har försökt lösa men vet inte om jag var på rätt väg med pyth sats?
Anika1 skrev:Ja det stämmer att CD ska vara 10, 7, hur kom du fram till det?
jag tror att man skall lösa med likformighet och behöver inte vinklarnas värde
Om vi utgår ifrån att ABC och CDE är likformiga, vilket de inte är:
likformighet: CD/(4+CE)=3/4
pythagoras: CE^2+3^2=CD^2
Två ekvationer, två okända, lös för CD.
Jaha kan man inte använda likformighet ojdå trodde att trianglarna var likformiga
Anika1 skrev:Jaha kan man inte använda likformighet ojdå trodde att trianglarna var likformiga
Jag tar tillbaka och hävdar motsatsen.
Vinkeln CDE är lika stor som BAE, sedan delar de C och har en rät vinkel.
De är alltså likformiga, men figuren är inte rättvisande.
Är AE 4 ? Får man det via Pythagoras sats
Anika1 skrev:Är AE 4 ? Får man det via Pythagoras sats
Absolut! Det är också en känd triangel med sidorna 3, 4 och 5. Självklart går det att räkna ut eftersom du har AD och DE.
Tack så jättemycket , du hjälpte verkligen bara på några minuter!
Men en sistaaa fråga hur fick du 3/4
för höjden 3 blir motsvarande sträcka inte 4 då den är i basen?
detta är min skiss stämmer ens den? 
3/4 är DE/AB, alltså kort katet / kort katet.
I din skiss är AB=5, men så är det inte.
Jaha ojdå är BD och AD 5
Anika1 skrev:Jaha ojdå är BD och AD 5
Nej, BD är inte 5. Trianglarna ABD och ADE är ju lika.
sictransit skrev:I din skiss är AB=5, men så är det inte.
Det hade jag också skrivit, i #4.
75/7?
Trinity2: ja.
Anika: I ditt första inlägg har du en mening på tre långa rader som gör mig yr i huvudet.
Öva gärna att dela upp resonemangen i korta meningar med radbyten, t ex
Pythagoras sats ger AE = 4 (3-4-5-triangel).
Triangel AED är kongruent med ADB (lika vinklar, gemensam hypotenusa), så AB = AE = 4 och BD = DE = 3.
Triangel DEC är likformig med ABC. Det ger ekvationerna
x/(y+4) = 3/4
y/(x+3)= 3/4
...
y= (4x/3) - 4 sätts in i den andra ekvationen.
...
x = 10 5/7
Louis skrev:Trinity2: ja.
Anika: I ditt första inlägg har du en mening på tre långa rader som gör mig yr i huvudet.
Öva gärna att dela upp resonemangen i korta meningar med radbyten, t ex
Pythagoras sats ger AE = 4 (3-4-5-triangel).
Triangel AED är kongruent med ADB (lika vinklar, gemensam hypotenusa), så AB = AE = 4 och BD = DE = 3.
Triangel DEC är likformig med ABC. Det ger ekvationerna
x/(y+4) = 3/4
y/(x+3)= 3/4
...
y= (4x/3) - 4 sätts in i den andra ekvationen.
...
x = 10 5/7
Tack. Bilden är felritad. AE och AB är tangenter till en cirkel med centrum i D varför de flesta sträckor faller ut direkt. Sedan gör man som du skrivit. När jag nu ser på bilden verkar inte ens DE vinkelrät mot AC...
Så här borde den ha sett ut, givet uppgifterna man fick.
.
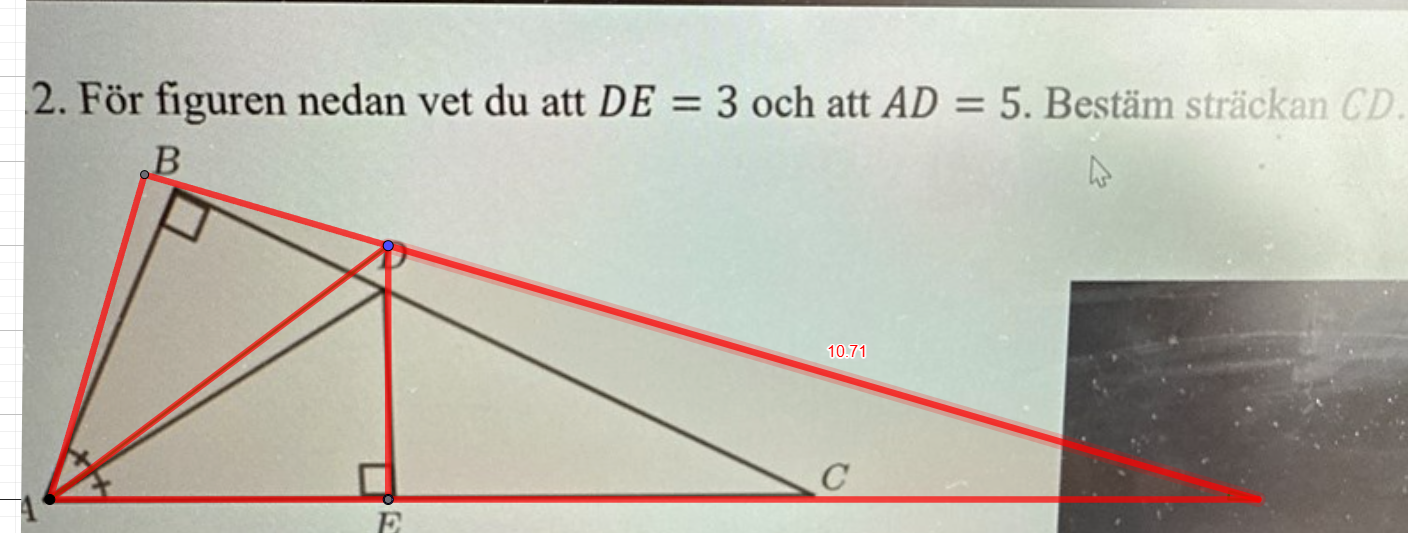
(feltänkt)
okej tack för all hjälp!
Bra att det löste sig till slut!
En liten slutkommentar:
Du kanske har råkat ut för fel i läroböckerna tidigare?
Jag har två tjejer, den äldsta i gymnasiet. Det är inte sällan jag upptäcker att uppgiften har en figur som inte stämmer med texten. Kanske har man tagit en figur som "verkar bra" och ändrat några siffror? Kanske har man en läroboksförfattare som knåpar ihop uppgiftens text och sedan en illustratör som ritar bilden. Illustratören är bra på att rita, men kanske sämre på matte.
Helt klart är att läroböcker inte korrekturläses längre, vilket är väldigt tråkigt.
Idag har man inte korr på dagstidningar heller, men det är inte lika illa. Läser jag en nyhet i lokaltidningen, kan jag sila stavfel och usel grammatik. Budskapet från journalisten går fram ändå, även om trovärdigheten sänks.
När figuren inte stämmer med texten i en lärobok, eller facit helt enkelt är fel, så är det mycket värre. Då är det inte så lätt för eleven som inte får ihop det att förstå varför.
Då kan man luras, som jag gjordes, att tro att tringlarna i din uppgift inte är likformiga. Läser man texten är de det. Tittar man på figuren så säger min magkänsla att CDE och ABC inte är ett dugg lika.
sictransit skrev:
Tittar man på figuren så säger min magkänsla att CDE och ABC inte är ett dugg lika.
Någonstans finns väl också en vits med att inte lita för mycket på figuren.
Var jag på rätt väg för att lösa uppgiften? Alltså mina tankegångar och vad jag brister i, så att jag kan öva inför mitt prov.
Såg du mitt inlägg #28. Dina tankar är inte helt lätta att följa.
Det handlar om Pythagoras och om likformighet, ja.
Men du skriver att du med likformighet tänker beräkna y.
I #3 verkar du dock räkna på två trianglar som inte är likformiga.
x och y kan inte beräknas var för sig. Du behöver ekvationer med både x och y.
Det har att göra med att du måste vända på triangel DEC för att använda likformigheten med ABC.
y i DEC motsvarar x+3 i ABC, så både x och y måste vara med. Se #28 igen.
Jaha okej förstår, tack!
sictransit skrev:Bra att det löste sig till slut!
En liten slutkommentar:
Du kanske har råkat ut för fel i läroböckerna tidigare?
Jag har två tjejer, den äldsta i gymnasiet. Det är inte sällan jag upptäcker att uppgiften har en figur som inte stämmer med texten. Kanske har man tagit en figur som "verkar bra" och ändrat några siffror? Kanske har man en läroboksförfattare som knåpar ihop uppgiftens text och sedan en illustratör som ritar bilden. Illustratören är bra på att rita, men kanske sämre på matte.
Helt klart är att läroböcker inte korrekturläses längre, vilket är väldigt tråkigt.
Idag har man inte korr på dagstidningar heller, men det är inte lika illa. Läser jag en nyhet i lokaltidningen, kan jag sila stavfel och usel grammatik. Budskapet från journalisten går fram ändå, även om trovärdigheten sänks.
När figuren inte stämmer med texten i en lärobok, eller facit helt enkelt är fel, så är det mycket värre. Då är det inte så lätt för eleven som inte får ihop det att förstå varför.
Då kan man luras, som jag gjordes, att tro att tringlarna i din uppgift inte är likformiga. Läser man texten är de det. Tittar man på figuren så säger min magkänsla att CDE och ABC inte är ett dugg lika.
Instämmer. Men, vi har - på alla nivåer - frångått granskning och kvalité. Det finns få förlagshus som har en redaktör värd titeln. Det är inte meningen att redaktören skall kontrollläsa och -räkna en bok (i många fall kan matematik vara så svårt att nästan ingen begriper den ändå, t.ex. det Springer Verlag ger ut), men redaktören skall hålla författaren "i örat". Idag tar förlagen emot en PDF, och skickar den till tryck. Det finns inte tid, pengar (eller intresse?) för "QA".
Man brukar skämtsamt citera Pólya:
"Geometry is the science of correct reasoning on incorrect figures."
Det låter skoj, men det är inte så skoj för studenten. Matematik är svårt nog som det är, med korrekta bilder.
